литография / 1_1_Литографические методы в нанотехнологии

m1(z,0)=m10 – начальная концентрация ингибитора

m2(z,t)=m20 – однородность и постоянство полимера, который не осветляется при экспонировании

m3(z,t)=m10-m1(z,t) – преобразование одного моля ингибитора в 1 моль продуктов реакции С их учетом получаем:

Экспериментально установлено, что скорость проявления фоторезиста в точке (x,z) может быть выражена через степень разрушения ингибитора в этой точке следующей зависимостью:

Полученное в предыдущем разделе распределение скоростей проявления V(x,z) по ячейкам экспонированного участка фоторезиста является основой для моделирования процесса проявления.

Процесс проявления можно описать, представив объем проявляемого фоторезиста в виде матрицы, состоящей из прямоугольных ячеек. Обычно при этом принимаются три главные гипотезы:

1. Проявитель не проникает за линию фронта проявления пленки, или, если такое проникновение и происходит, то виде диффузии на расстояния порядка размера элементарной молекулы полимера (~100A)

Рис. 19. Пространственно-временные изменения в фоторезисте

при экспонировании

2.Действие проявителя постоянно в объеме ячейки, при этом продукты распада нейтральны по отношению к воздействию проявителя.

3.Процесс проявления осуществляется "погружением", без механического воздействия на фоторезист, например, струйным проявлением.

В данной работе реализован алгоритм проявления на основе «удаления ячеек», который сочетает простоту реализации с достаточной точностью получаемых результатов.

Выбранный алгоритм основан на следующих основных положениях.

Скорость проявления V( x,z ) определенная из модели, не зависит от ориентации фронта проявления, так как всегда направлена по нормали к этому фронту. Однако смещение фронта за единицу времени на V( x,z ) по нормали к фронту приведет к изменению координат точек по вертикали z на величину z V( x,z ) / cos (рис.20,

а). Проявление начинается с верхней поверхности пленки фоторезиста. Предварительно каждой ячейке рассматриваемого объема в зависимости от степени деструкции в ней ингибитора присвоена соответствующая скорость проявления.

После прохождения начального цикла (растворение ячеек на поверхности пленки) вводятся корректирующие коэффициенты, учитывающие число сторон ячейки, подвергающихся одновременному воздействию проявителя.

После каждого временного цикла матрица, характеризующая состояние ячеек, обновляется и, при необходимости, запоминается, что позволяет наглядно выводить информацию о протекании процесса проявления.

Ячейка считается проявленной, если для заданного временного интервала приданная ей скорость обеспечивает растворение всего ее объема или большей его части. Когда ячейка проявлена полностью, она открывает для воздействия проявителя соседние ячейки, которые далее рассматриваются как вошедшие в фазу проявления. Для назначения оптимального временного интервала следует предварительно оценить максимальное в данном объеме время проявления Vmax и учесть влияние геометрического расположения ячеек при проявлении (рис. 20 , б).

Время проявления (i,j)-й ячейки является функцией:

-скорости Vi,j

-размеров ячейки x, z

-геометрического расположения поверхности ячейки i,j

-вида контакта с проявителем и исходного состояния ячейки.

Время проявления ячейки (i,j) зависит от состояния четырех смежных ячеек: (i+1, j), (i-1, j), (i, j -1), (i, j+1).Это состояние обозначается 0 или 1. Если ячейка (i,j) еще не проявлена, то ее состояние обозначается. Если ячейка полностью пустая, т.е. проявлена, то ее состояние обозначается ij 1.

Рис. 20. Проявление позитивного фоторезиста:

а- фронт проявления, б - ячейка фоторезиста

Сучетом этих обозначений первоначальное время проявления в одной полной ячейке рассчитывается по формуле:

Эта формула включает восемь вариантов состояний смежных ячеек, представленных на рис.3.10. В результате для проявления ячейки высотой z требуется время , определяемое из выражения

Моделирование фронта проявления осуществляется последовательно, шаг за шагом. Интервал приращения времени рассчитывается исходя из максимальной скорости

проявления в ячейках 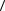ij .

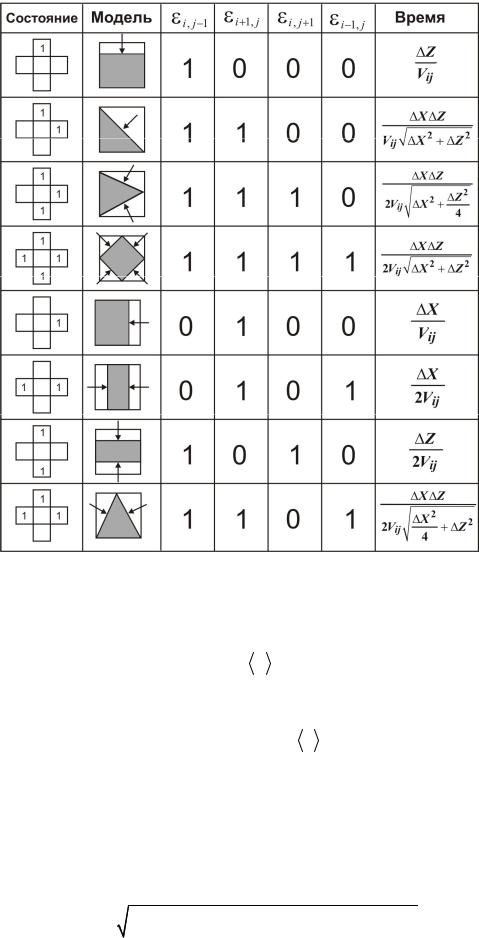
Рис. 21. Состояния ячеек позитивного фоторезиста при проявлении

Относительный объем ячейки, оставшийся после истечения времени <t>,

После проведения каждой итерации матрица, содержащая информацию об остаточных объемах ячеек, обновляется. Очередная обновленная матрица состояний анализируется и для каждой ячейки, у которой появляется одна или несколько новых свободных сторон, корректируется время, требуемое для ее проявления в текущей итерации:

В зависимости от степени разрушения ячеек профиль проявления постепенно изменяется. Расчет завершается, когда относительные изменения становятся меньше заданной величины.