
Исследование высокочастотных катушек индуктивности
..pdf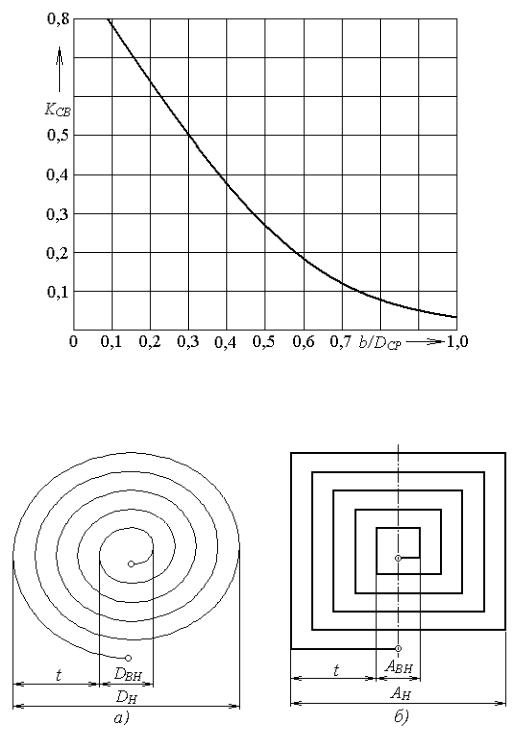
|
|
2 |
|
|
|
|
|
|
|
|
|
|
L = 24,75 × DСР × N |
5 / 3 |
æ |
4DСР ö |
×10 |
−7 |
|||||
|
|
× lgç |
t |
÷ |
|
||||||
|
|
|
|
|
|
è |
ø |
|
|
||
|
L = 5,55 × AСР × N |
5 / 3 |
æ |
8AСР ö |
×10 |
−7 |
|||||
|
|
× lgç |
t |
÷ |
|
||||||
|
|
|
|
|
|
è |
ø |
|
|
||
где |
DСР = DН + DВН , |
AСР |
= |
AН + AВН |
. |
|
|
|
|||
|
|
|
|
||||||||
|
2 |
|
2 |
|
|
|
|
|
|
||
,
,
(Б.7)
(Б.8)
Рисунок Б.5 – Зависимость коэффициента связи от соотношения b/DСР для многослойных секционированных катушек
Рисунок Б.6 – Конструкции плоских печатных катушек
Индуктивность цилиндрической катушки с экраном равна

2 |
|
LКЭ = LК(1 – KСВ2), |
(Б.9) |
где LК - индуктивность катушки без экрана; KСВ - коэффициент связи катушки |
|
с экраном. |
|
Для однослойных и тонких многослойных катушек коэффициент связи |
|
может быть определён по эмпирической формуле |
|
KСВ2 » h×(D/DЭ)3, |
(Б.10) |
где h - коэффициент, зависящий от конструктивных |
размеров катушки, |
определяется по рисунку 7; D/DЭ - отношение внешнего диаметра катушки к внутреннему диаметру экрана.
Рисунок Б.7 – Зависимость коэффициента h от соотношения l/D
Для многослойных катушек со значительной глубиной намотки коэффициент связи равен
|
( D¢ / D)3 |
, |
(Б.11) |
KСВ = |
L0 × L0Э × [1 + (lЭ / DЭ )2 ] |
где L0 и L0Э- соответствующие коэффициенты для катушки и экрана, определяемые по рисунку 1 и по таблице 1; lЭ и DЭ- длина и внутренний
диаметр экрана; D¢ - приведённый диаметр катушки с экраном, равный
= |
|
|
|
|
|
. |
(Б.12) |
( |
+ |
DЭ3 |
) |
/ 2 |
|||
D′ 3 D3 |
|
|
|
|
|||
Индуктивность катушки с ферромагнитным сердечником увеличивается |
|||||||
в mС раз |
|
|
|
|
|
|
|
LКС = mС ×L, |
|
(Б.13) |
|||||
где mС - действующая магнитная проницаемость сердечника (справочная величина).
2

2 |
|
2 РАСЧЁТ ДОБРОТНОСТИ |
|
Добротность ВКИ определяется соотношением |
|
Q = wL / rL, |
(Б.14) |
где w = 2pf – круговая частота; rL – сопротивление, эквивалентное полным активным потерям в катушке
RL = rf + DrД + DrС +DrЭ. |
(Б.15) |
Здесь DrД, DrС, DrЭ – эквивалентные сопротивления потерь, |
вносимые |
диэлектриком, экраном и сердечником, соответственно. |
|
Для цилиндрических катушек на частотах до 10 МГц |
|
é
rf =r0 × êF( z )
êë
æ K × N ×d ö2 |
ù |
, |
(Б.16) |
|||
+ç |
2D |
÷ |
×G( z )ú |
|||
è |
ø |
|
ú |
|
|
|
|
|
|
|
û |
|
|
где r0 – сопротивление провода |
постоянному току; |
F(z) |
и G(z) |
– |
|
коэффициенты, учитывающие |
влияние |
поверхностного |
эффекта |
и |
|
эффекта близости на увеличение активного сопротивления, находится из таблицы 2; K– коэффициент, учитывающий влияние размеров катушки на эффект близости, определяется по графикам рисунка 8; d – диаметр провода
без изоляции; D – диаметр однослойной катушки или |
наружный |
диаметр |
||||||||
многослойной катушки; z – вспомогательный расчётный параметр |
|
|||||||||
|
|
|
z =10 ,6 ×d |
|
. |
|
|
|
(Б.17) |
|
|
|
|
f |
|
|
|
||||
Таблица Б.2 - Значения коэффициентов F(z) и G(z) |
|
|
||||||||
z |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
||
F(z) |
1 |
1,005 |
1,026 |
1,078 |
1,175 |
1,318 |
1,492 |
1,678 |
||
G(z) |
0,001 |
0,015 |
0,069 |
0,0172 |
0,295 |
0,405 |
0,499 |
0,584 |
||
z |
4,5 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
||
F(z) |
1,863 |
2,043 |
2,394 |
2,743 |
3,094 |
3,446 |
3,799 |
4,151 |
||
G(z) |
0,669 |
0,755 |
0,932 |
1,109 |
1,287 |
1,464 |
1,641 |
1,818 |
||
z |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
||
F(z) |
4,504 |
4,856 |
5,209 |
5,562 |
5,915 |
6,268 |
6,621 |
6,974 |
||
G(z) |
1,995 |
2,171 |
2,384 |
2,525 |
2,702 |
2,879 |
3,056 |
3,232 |
||
z |
20 |
21 |
22 |
23 |
24 |
25 |
30 |
40 |
||
F(z) |
7,328 |
7,681 |
8,034 |
8,388 |
8,741 |
9,094 |
10,86 |
14,4 |
||
G(z) |
3,409 |
3,586 |
3,763 |
3,936 |
4,117 |
4,317 |
5,177 |
6,946 |
||
z |
50 |
60 |
70 |
80 |
90 |
100 |
z >100 |
|||
F(z) |
17,93 |
21,46 |
25,0 |
28,54 |
32,07 |
35,61 |
0,354×z+ 0,25 |
|||
G(z) |
8,173 |
10,48 |
12,25 |
14,02 |
15,78 |
17,75 |
0,177×z− 0,125 |
|||

2
Рисунок Б.8 – Зависимости коэффициента K от соотношения l/D для однослойных и тонких многослойных катушек с числом слоёв m
Для катушек КВ и УКВ с шаговой намоткой в диапазоне частот свыше 10 МГц сопротивление провода току высокой частоты можно определить по приблизительной формуле
|
rf =0,525 ×N ×D × |
|
×10−6 / d . |
|
(Б.18) |
|||
|
f |
|
||||||
Сопротивление |
круглого |
провода |
|
постоянному |
току |
для |
||
цилиндрических катушек равно |
|
|
|
|
, |
|
(Б.19) |
|
|
r |
=4 ×r×N ×D |
/ d 2 |
|
||||
|
0 |
|
|
СР |
|
|
|
|
где DСР – средний диаметр обмотки катушки. |
|
|
|
|
||||
Удельное сопротивление медного провода r = 1,75×10-8 Ом×м, тогда |
|
|||||||
|
r0 = 7×N×DСР×10-8/ d2. |
|
|
(Б.20) |
||||
Оптимальный диаметр провода, соответствующий минимуму сопротивления rf , может быть рассчитан по следующей простой методике:
1) определяется вспомогательный параметр

2
z′=10,6 
 f ;
f ;
2) рассчитывается вспомогательный коэффициент
æ |
K × N ö2 |
; |
|
y=ç |
|
÷ |
|
|
|||
è |
2 × z¢× D ø |
|
|
(Б.21)
(Б.22)
3) по графику (рисунок 9) находится оптимальная величина параметра
zОПТ;
4) определяется оптимальный диаметр провода |
|
dОПТ = zОПТ / z¢. |
(Б.23) |
Рисунок Б.9 – Зависимость zОПТ от коэффициента ψ
Сопротивление, вносимое потерями в диэлектрике, может быть ориентировочно рассчитано по формуле
DrД »0,25 ×C0 Д ×tgd×L2 × f 3 ×103 , |
(Б.24) |
где C0Д – собственная ёмкость катушки через диэлектрик, приближённо равна полной величине собственной ёмкости; tgd – тангенс угла потерь в
диэлектрике, справочная величина (3, таблица П-1).
Сопротивление, вносимое экраном, определяется сопротивлением потерь в экране r¢Э и ослаблением влияния эффекта близости на
сопротивление обмотки r²Э |
|
|
|
|
|
|
|
|
где |
rЭ = |
r¢Э – |
r¢¢Э, |
; |
(Б.25) |
|||
Dr¢ =K 2 |
× N 2 |
×r ×(D / D |
Э |
) |
(Б.26) |
|||
|
Э СВ |
|
Э |
|
|
|
|
|

2
Dr¢¢ =r ×(2 -K 2 |
)× K 2 |
||
Э |
0 |
СВ |
СВ |
æK × N × d ö2 |
(Б.27) |
|||
×ç |
2 × D |
÷ |
×G(z) . |
|
è |
ø |
|
|
|
Здесь rЭ – сопротивление внутренней поверхности экрана; DЭ – внутренний диаметр экрана.
rЭ » p×rЭ×DЭ / (lЭ×xЭ), |
(Б.28) |
где rЭ – удельное сопротивление материала экрана или материала покрытия
внутренней части экрана; lЭ – длина (высота) экрана; xЭ – глубина проникновения вихревых токов в экране
|
xЭ =0,5 × |
|
|
|
. |
|
|
(Б.29) |
|||
|
rЭ / f |
|
|||||||||
С учетом (28) и (29) вносимое сопротивление экрана будет равно |
|
||||||||||
Dr¢ |
=2 × p× K 2 |
× N 2 |
D |
|
× |
|
×10−3 |
. |
(Б.30) |
||
|
r × f |
||||||||||
|
|||||||||||
Э |
СВ |
|
|
lЭ |
|
Э |
|||||
|
|
|
|
|
|
|
|
|
|||
Сопротивление потерь, вносимое ферромагнитным сердечником, обусловлено активными потерями на гистерезис, вихревые токи и последствие и может быть определено через общий угол потерь в сердечнике
dС |
|
DrС = 2pf×LКС×tgdС , |
(Б.31) |
где LКС – индуктивность катушки с сердечником. |
|
3 РАСЧЁТ СОБСТВЕННОЙ ЁМКОСТИ
Собственную ёмкость однослойной катушки, с удовлетворительной точностью можно рассчитать по формуле
С0 » |
p× D ×10−10 |
|
|
, |
(Б.32) |
|
8,31×lg( a + a2 |
-1 ) |
|||||
|
|
|
|
|
|
|
где a = t /d - отношение шага намотки к диаметру провода без изоляции. Ёмкость однослойной катушки, намотанной на гладкий каркас,
диэлектрическая проницаемость которого лежит в пределах e =4…6, может
быть рассчитана приближенно по формуле |
|
C0 » K1×K2×D×10-10, |
(Б.33) |
где K1 и K2 - коэффициенты, зависящие от шага намотки t и соотношения l/D,
определяются по графикам из рисунка 10.
Если материал каркаса отличается от указанной выше величины, то собственную ёмкость следует пропорционально увеличить или уменьшить.
Для катушек с нарезным каркасом ёмкость увеличивается на 20-25 % в зависимости от глубины нарезки, а у катушек с ребристым каркасом C0 меньше на 15-20 %. Пропитка и обволакивание катушек приводят к увеличению ёмкости на 20-30 %.
Собственная ёмкость многослойных катушек с простой намоткой
C0 » p×DСР×(8,45×e + 8,23)×10-12, |
(Б.34) |
гдеDСР – средний диаметр намотки; e – диэлектрическая проницаемость изоляции провода.

2
Рисунок Б.10 – Коэффициенты K1 и K2 для расчета собственной емкости однослойных катушек
Для секционированных катушек
C0 » C0С×(0,33×n + 0,67) / n, (Б.35) где C0С× – ёмкость секции; n – число секций.
