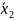Министерство цифрового развития, связи и массовых коммуникаций
Российской Федерации Ордена Трудового Красного Знамени
федеральное государственное бюджетное образовательное
учреждение высшего образования
Московский технический университет связи и информатики
Кафедра Информатики
Лабораторная работа №3
по дисциплине «Математическая логика и теория алгоритмов»
Тема: «Минимизация логических выражений»
Вариант №4
Москва 2021
Содержание
Вывод 11
Список использованных источников 11
Задание 1. Написать минимальное выражение для заданной таблицы истинности и нарисовать по нему логическую схему.
Решение:
Построение СДНФ
Составление карты Карно:
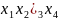
00
01
11
10
00
0
0
0
1
01
0
0
1
0
11
1
0
0
0
10
0
0
0
0
Сцепление единиц
Количество клеток, входящих в одну группу, должно выражаться числом кратным 2, т.е. 2m где m=0,1,2... В данном случае, m = 0 20=1. То есть, максимальное количество клеток, входящих в одну группу, равняется единице, поэтому дальнейшая минимизация невозможна.
Составление логической схемы:
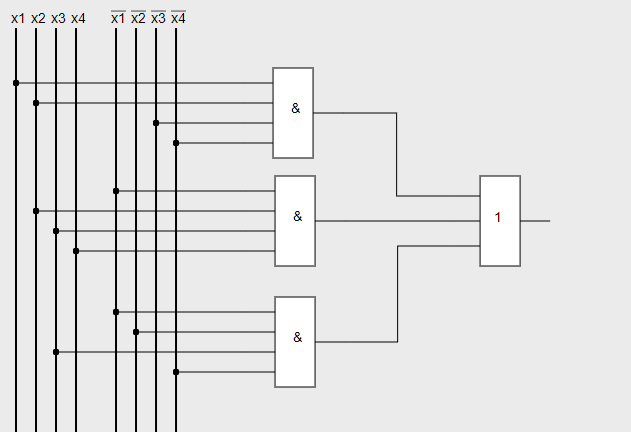
Задание 2. Для заданного логического выражения написать каноническую сумму минтермов и нарисовать минимальную логическую схему. Указание: логическое выражение записывается по следующему принципу. Знаку "+" в строке варианта соответствует указанное в шапке таблицы полное логическое произведение. В это произведение переменные входят в инверсном или прямом виде в соответствии с указанным кодом. Например, для варианта 1 первому в этой строке знаку "+" соответствует 0 для кода abcd, поэтому первым слагаемым в логическом выражении является произведение всех переменных, взятых с инверсией, так как код нуля в четырехразрядном формате записывается как 0000 и т.д.
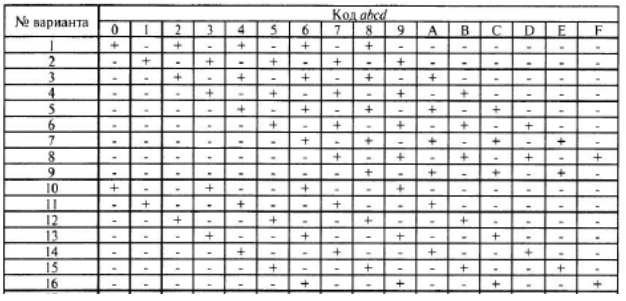
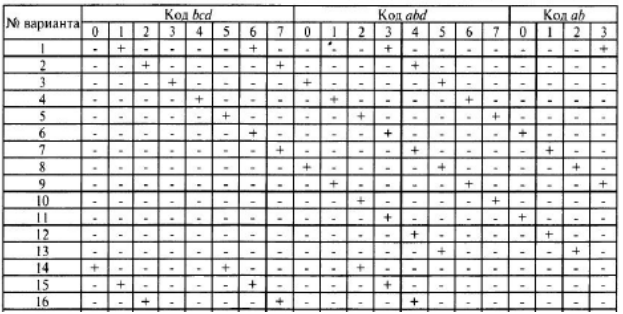
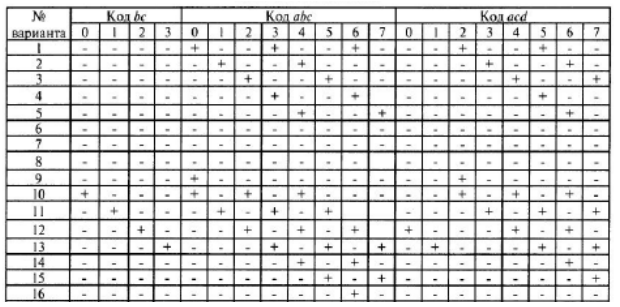
Решение:
По представленным таблицам составим логическую функцию.
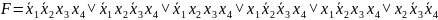
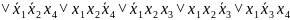
Чтобы написать СДНФ для данной логической функции, необходимо составить таблицу истинности. Пронумеруем функции от 1 до 11 для записи в таблицу истинности.
1)
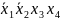
2)
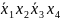
3)
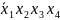
4)
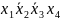
5)
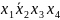
6)
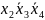
7)
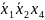
8)
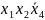
9)
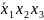
10)
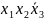
11)
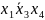
Таблица истинности
a |
b |
c |
d |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
F |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 Построение сднф
2) Составление Карты Карно:
|
00 |
01 |
11 |
10 |
00 |
0 |
1 |
1 |
0 |
01 |
1 |
1 |
1 |
1 |
11 |
1 |
1 |
0 |
1 |
10 |
0 |
1 |
1 |
0 |
3) Сцепление единиц
Используемые правила для склеивания единиц:
Каждая клетка, входящая в группу из
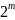 клеток, должна иметь m соседних в группе
(для 1-ой группы – m=2,
для 2-ой – m=1, для 3-ей – m=1, для 4-ой –
m=1).
клеток, должна иметь m соседних в группе
(для 1-ой группы – m=2,
для 2-ой – m=1, для 3-ей – m=1, для 4-ой –
m=1).Каждая клетка должна входить хотя бы в одну группу (Выполняется).
В каждую группу должно входить максимальное число клеток, т.е. ни одна группа не должна содержаться в другой группе (Например, для второй группы задействовано свойство, что карта Карно является сферой и могут быть соединены клетки на противоположных частях карты).
Число групп должно быть минимальным (4 группы – минимальное количество).
Первая группа:
|
00 |
01 |
11 |
10 |
00 |
0 |
1 |
1 |
0 |
01 |
1 |
1 |
1 |
1 |
11 |
1 |
1 |
0 |
1 |
10 |
0 |
1 |
1 |
0 |
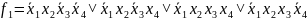
Вторая группа:
|
00 |
01 |
11 |
10 |
00 |
0 |
1 |
1 |
0 |
01 |
1 |
1 |
1 |
1 |
11 |
1 |
1 |
0 |
1 |
10 |
0 |
1 |
1 |
0 |
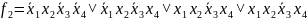
Третья группа:
|
00 |
01 |
11 |
10 |
00 |
0 |
1 |
1 |
0 |
01 |
1 |
1 |
1 |
1 |
11 |
1 |
1 |
0 |
1 |
10 |
0 |
1 |
1 |
0 |
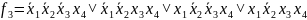
Четвертая группа:
|
00 |
01 |
11 |
10 |
00 |
0 |
1 |
1 |
0 |
01 |
1 |
1 |
1 |
1 |
11 |
1 |
1 |
0 |
1 |
10 |
0 |
1 |
1 |
0 |
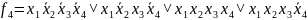
Считывание МСДНФ:
Считывание функции F по группе склеивания происходит по следующему принципу: переменные, которые сохраняют одинаковые значения в группе склеивания входят в конъюнкцию, причем значениям 1 соответствуют сами переменные, а значениям 0 их отрицания.
В первую группу входят переменные
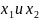 ,
поскольку они не изменяются в рамках
этого прямоугольника, причем переменная
,
поскольку они не изменяются в рамках
этого прямоугольника, причем переменная
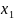 входит в группу с инверсией. В итоге
первая группа объединяется в выражение:
входит в группу с инверсией. В итоге
первая группа объединяется в выражение:
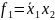
Во вторую группу входят переменные
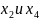 .
В рамках этого квадрата
.
В рамках этого квадрата
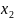 сохраняют значение 1 и входят в группу
без инверсии, переменная
сохраняют значение 1 и входят в группу
без инверсии, переменная
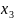 сохраняет значение 0 и входит в группу
с инверсией. В итоге вторая группа
объединяется в выражение:
сохраняет значение 0 и входит в группу
с инверсией. В итоге вторая группа
объединяется в выражение:

В третью группу входят переменные
.
В рамках этого квадрата
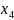 сохраняет значение 1 и входят в группу
без инверсии, переменная
сохраняет значение 0 и входит в группу
с инверсией. В итоге третья группа
объединяется в выражение:
сохраняет значение 1 и входят в группу
без инверсии, переменная
сохраняет значение 0 и входит в группу
с инверсией. В итоге третья группа
объединяется в выражение:
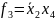
В четвертую группу входят переменные
.
В рамках этого квадрата
сохраняет значение 1 и входит в группу
без инверсии, переменные
сохраняет значение 0 и входят в группу
с инверсией. В итоге четвертая группа
объединяется в выражение:
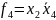
Сумма выражений
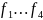 соответствует МСДНФ:
соответствует МСДНФ:
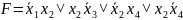
Задание 3. минимизировать заданную логическую схему и написать соответствующую каноническую сумму минтермов.
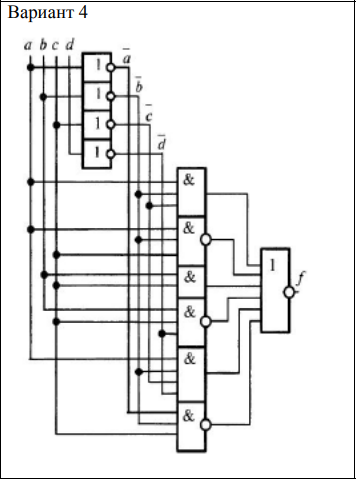
Решение:
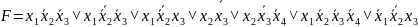
Чтобы написать СДНФ для данной логической функции, необходимо составить таблицу истинности. Пронумеруем функции от 1 до 6 для записи в таблицу истинности.
1)
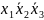
2)
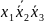
3)
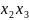
4)
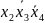
5)
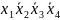
6)
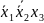
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
F |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
Из таблицы истинности следует, что F=0
Вывод
Подводя итог, я научился минимизировать логические выражения с помощью карты Карно.