Практическая_2

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра АПУ

отчет

по практической работе №2

по дисциплине «Теория автоматического управления»

Тема: Соединение звеньев

Вариант № 1

Студент гр. 8091		Гришин И. Д.
Преподаватель		Брикова О. И.

Санкт-Петербург

2022

Задание 1.

Определить характеристики в корневой, временной и частотной областях последовательного соединения двух устойчивых апериодических звеньев первого порядка 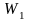и 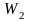с параметрам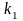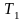и , и 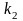, 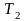соответственно (см. варианты заданий).

Рассчитать параметры 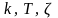ПФ эквивалентного звена второго порядка, записанной в виде:

.

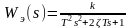Согласно, варианту:

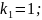
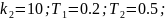
Запишем передаточные функции апериодических звеньев первого порядка:

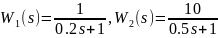
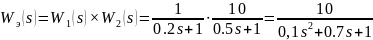
(c),

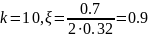
Схема соединения приведена на рисунке 1:

Рис.1 схема последовательного соединения звеньев 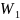и

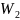
Характеристики в корневой, временной и частотной областях последовательного соединения двух устойчивых апериодических звеньев первого порядка и на рис. 2.

а) б)

В) Г)

Рис.2. Характеристики в корневой, временной и частотной областях последовательного соединения звеньев и

а) Реакция на единичный импульс; б) ЛАЧХ и ЛФЧХ; в) АФХ;

г) Характеристика в корневой области

Вопросы.

1. Какой вид имеет асимптотическая логарифмическая амплитудно-частотная характеристика (ЛАЧХ) соединения (привести график) и ?

Рис. 3 ЛАЧХ последовательного соединения звеньев

Рис. 4 ЛАЧХ звена

2. В чём состоят различия переходных и частотных (амплитудно-фазовых характеристик (АФХ), логарифмических частотных характеристик (ЛЧХ)) характеристик апериодического звена и соединения звеньев 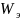? Привести графики и дать подробный анализ. При анализе обратить внимание: на установившиеся значения переходных характеристик; на длительность переходных процессов; на то, в каких квадрантах комплексной плоскости располагаются АФХ; чем отличаются ЛЧХ на низких и высоких частотах; по ЛАЧХ сравнить фильтрующие свойства и .

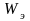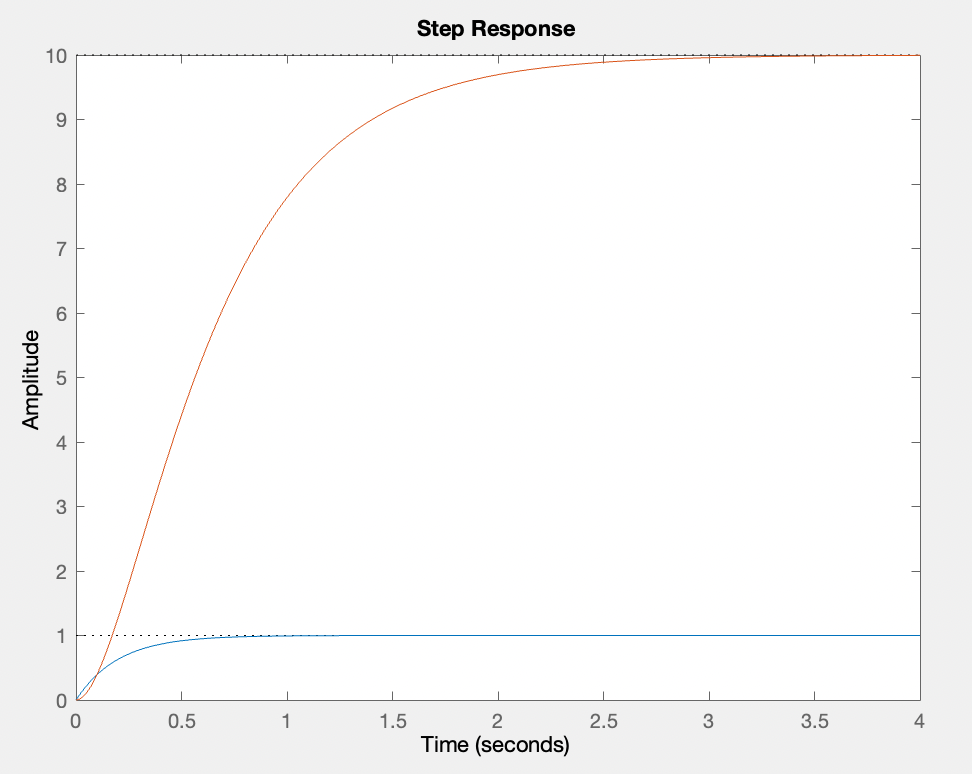
Рис. 5 Переходная характеристика (красная линия), (голубая линия)

Рис. 6 ЛАЧХ (красная линия), (голубая линия)

Рис. 7 Годограф Найквиста (красная линия), (голубая линия)

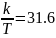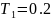
Производная реакции на единичную ступенчатую функцию (Рис.5) звена имеет в нуле значение 0, в отличие от , у которой она равна . Это связано с наличием двух простых ненулевых корней ХП звена , и, соответственно, двух переходных процессов с разными постоянными времени: 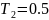. Установившиеся значения равны коэффициентам усиления, т. е. 10 и 1 соответственно для звеньев , . Длительность переходного процесса больше у апериодического звена 2-го порядка .

АФХ располагается в третьем и четвертом квадрантах. АФХ , располагается только в четвертом квадранте (Рис. 7).

На низких частотах ЛЧХ обоих ПФ мало отличаются, однако усиливает сигнал, а нет. На высоких частотах больше проявляются фильтрующие свойства звена второго порядка, его ЛАЧХ проходит ниже. Предельное значение ФЧХ у и составляют соответственно 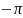и .

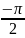1. Какое из двух звеньев и оказывает большее влияние на длительность затухания переходного процесса и почему?

Звено имеет большую длительность переходных процессов, т. к. постоянная времени 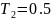больше постоянной времени звена 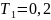. Следовательно, оно оказывает большее влияние на длительность процессов затухания .

Задание 2.

Определить характеристики в корневой, временной и частотной областях последовательного соединения двух звеньев с ПФ.

, .

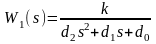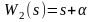Согласно, варианту:

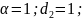
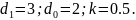
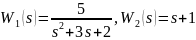
Характеристики в корневой, временной и частотной областях последовательного соединения двух звеньев и на рис. 8.

А) Б)

В) Г)

Рис. 8 Характеристики соединения звеньев и

а) Реакция на единичный импульс; б) ЛАЧХ и ЛФЧХ; в) АФХ;

г) Характеристика в корневой области

Вопросы.

1. Какому типовому звену соответствуют переходная и частотные характеристики соединения?

Устойчивому апериодическому звену первого порядка, т. к. вид ПФ после устранения диполя:

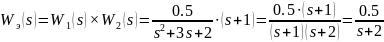
1. Является ли система второго порядка с ПФ 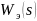полностью управляемой и наблюдаемой? Объяснить почему.

С помощью MATLAB найдем матрицы ФПС для данной системы (ss):

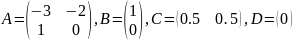
Найдем матрицу управляемости системы (ctrb):

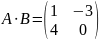
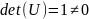
Определитель матрицы управляемости не равен нулю, значит, система полностью управляема.

Найдем матрицу наблюдаемости системы (obsv):

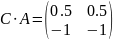
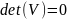
Определитель матрицы наблюдаемости равен нулю, значит, система не полностью наблюдаема.

Задание 3.

Определить характеристики в корневой, временной и частотной областях звена с ПФ вида

.

Рассчитать ПФ 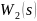звена, последовательное включение которого со звеном 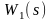компенсирует его правый полюс (компенсация происходит, когда в корневой плоскости на полюс накладывается нуль, т. е. происходит образование диполя).

Согласно варианту:

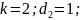
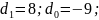
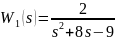
Характеристики в корневой, временной и частотной областях звена 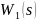на рисунке 9.

А) Б)

В) Г)

На рисунке 9 г видно, что ПФ звена имеет 1 правый полюс. Чтобы его скомпенсировать, необходимо создать в диполь, соединив последовательно со звеном звено .

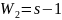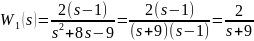
Вопросы:

3. 1. Как проявляются свойства неустойчивой части в последовательном соединении звеньев и на характеристиках соединения в целом с ПФ ?

Появляется полюс в правой полуплоскости, в результате образуется диполь.

2. . Как отражается на характеристиках соединения с ПФ 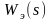в корневой, временной и частотной областях неполная компенсация неустойчивого полюса ПФ (неполная компенсация происходит в том случае, когда соответствующие нуль и полюс не совпадают, хотя могут быть близкими, т. е. располагаться на плоскости корней друг относительно друга на сколь угодно малом расстоянии)?

В корневой: левый полюс первого звена остался некомпенсированным; во временной: переходная характеристика возрастает со временем; в частотной: изменение фазовой характеристики начинается с –π.

Задание 4.

Найти ПФ 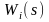типовых звеньев, параллельные соединения которых описываются эквивалентными дифференциальными уравнениями вида:

;

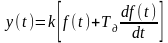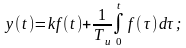
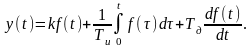
Согласно варианту:

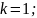
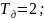
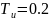
Построить асимптотические ЛАЧХ и логарифмические фазочастотные характеристики (ЛФЧХ).

Какие фильтрующие свойства проявляют звенья на низких и высоких частотах?

Соединение параллельное, тогда W_э(s)=W₁(s)+W₂(s)

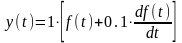
W_э(s)=k(1+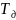 s) – пропорционально-дифференцирующее звено

W_э(s)=1+2s

Рис. 17. Логарифмические частотные характеристики: точные и асимптотические ЛАЧХ (сверху) и ЛФЧХ (снизу)

На низких частотах сигнал проходит без искажений (ЛАЧХ равна 0), высокие частоты усиливаются – это фильтр высоких частот.

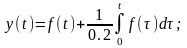
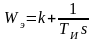- изодробное звено,

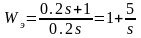
Рис 18. Логарифмические частотные характеристики: точная и асимптотическая ЛАЧХ (сверху) и ЛФЧХ (снизу)

На высоких частотах сигнал проходит без изменений (ЛАЧХ равна 0), низкие частоты усиливаются — это фильтр низких частот.

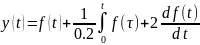
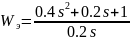
Рис. 19. Логарифмические частотные характеристики: точная и асимптотическая ЛАЧХ (сверху) и ЛФЧХ (снизу)

По графикам на рисунке 19 видно, что система усиливает сигнал на низких и высоких частотах, на частотах, близких к 5 рад/сек, сигнал проходит почти без изменений.