
ИССЛЕДОВАНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ 2 лаба по ТПС
.docxФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
Федеральное Государственное Бюджетное Образовательное Учреждение
Высшего Профессионального Образования
«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ ИМПЕРАТОРА АЛЕКСАНДРА I»
(ФГБОУ ВПО ПГУПС)
Кафедра «Электрическая связь»
ЛАБОРАТОРНАЯ РАБОТА №2
«ИССЛЕДОВАНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ»
Выполнил:
Проверил:
доктор технических наук
Санкт-Петербург
2022
ЦЕЛЬ РАБОТЫ: Знакомство с основными методами оценивания основных частотных параметров детерминированных сигналов, а также приобретение практических навыков работы в программной среде MATLAB.
Изучение синтаксиса построения функций в программной среде Matlab
Одиночный импульс Imp

Рисунок 1. Одиночный импульс
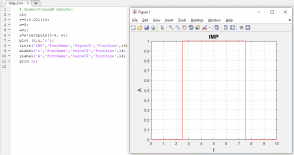
Рисунок 2. Изменение параметров одиночного импульса
На рисунке 1 показаны изменения ширины и начальной фазы импульса. За ширину импульса отвечает переменная W, за начальную фазу – аргумент t-5 в параметрах функции rectpuls(). Переменная t является вектором, отсчитывающим числа от нуля до 10 с шагом 001, она необходима для построения временной оси X. Переменная a определяет амплитуду создаваемого импульса. Plot() – функция, отвечающая за построение графика.

Рисунок 3. Изменение формы одиночного импульса
Серия импульсов Imp_ser
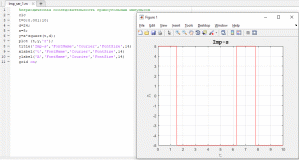
Рисунок 4. Серия импульсов
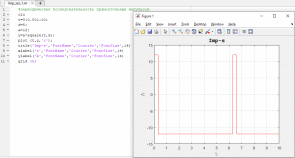
Рисунок 5. Изменение параметров серии импульсов
На рисунке 5 изображено изменение параметров серии импульсов. В данном примере переменная а отвечает за амплитуду импульсов, d определяет ширину импульсов.
На рисунке 6 представлено изменение времени наблюдения серии импульсов, а также их форма.
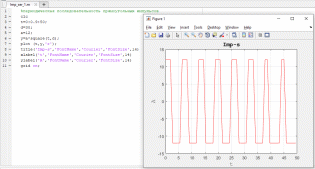
Рисунок 6. Изменение параметров серии импульсов
Дискретное преобразование Фурье прямоугольного импульса
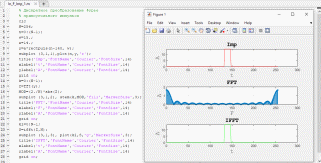
Рисунок 7. Дискретное преобразование прямоугольного импульса
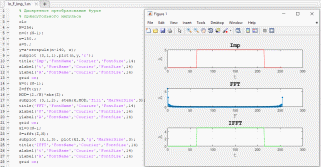
Рисунок 8. Дискретное преобразование прямоугольного импульса
На рисунке 8 изображено изменение параметров импульса при его дискретном преобразовании. В частности была изменена ширина импульса, путем присвоения нового значения переменной w, а также амплитуда импульса (переменная а).
На рисунке 9 представлено изменение времени наблюдения дискретного преобразования.
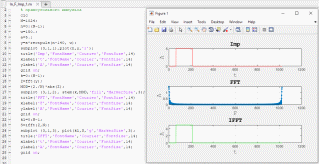
Рисунок 9. Изменение времени наблюдения дискретного преобразования.
Дискретное преобразование Фурье последовательности прямоугольных импульсов
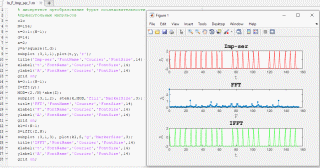
Рисунок 10. Дискретное преобразование последовательности прямоугольных импульсов.
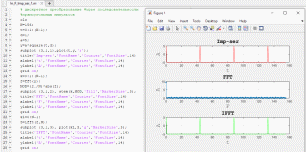
Рисунок 11. Изменение количества импульсов и амплитуды последовательности импульсов
В данном примере (рисунок 11) было изменено количество импульсов в последовательности путем изменения переменной d, отвечающей за процент периода сигнала, в котором прямоугольная волна положительна (рабочий цикл). На рисунке 12 изображена последовательность импульсов в значением рабочего цикла 50 процентов.
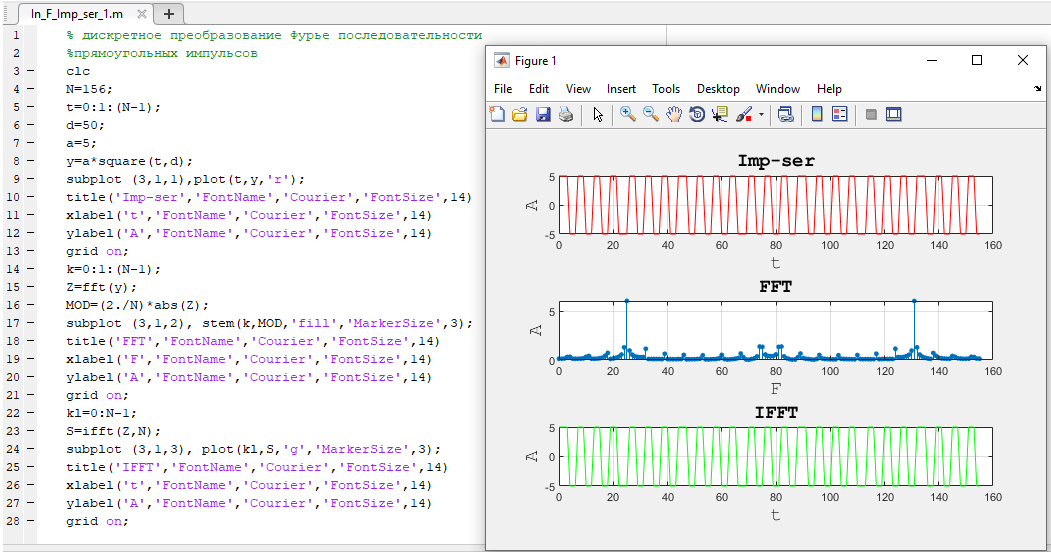
Рисунок 12. Значение duty равно 50%
Дискретное преобразование Фурье радиоимпульса с гауссовской огибающей
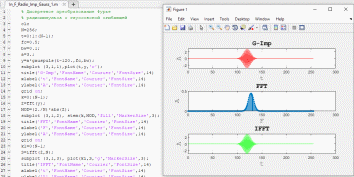
Рисунок 13. Дискретное преобразование Фурье радиоимпульса с гауссовской огибающей
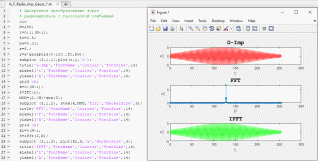
Рисунок 14. Изменение ширины радиоимпульса и его амплитуды
На рисунке 14 изображено изменение ширины радиоимпульса и его амплитуды. Такие изменения получены благодаря изменениям переменных fc, которая отвечает за частоту сигнала, и bw, которая носит название «Дробная полоса пропускания» и имеет вид действительной положительной скалярной величины.
На рисунке 15 изображено изменение времени наблюдения радиоимпульса, а также его смещение по оси времени.
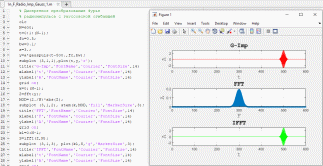
Рисунок 15. Изменение времени наблюдения, а также смещение импульса по оси времени
Дискретное преобразование Фурье треугольного импульса
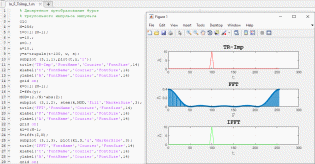
Рисунок 16. Дискретное преобразование треугольного импульса
На рисунке 17 изображено изменение ширины одиночного треугольного импульса, а также увеличена скошенность его заднего фронта. Эти изменение были достигнуты путем изменения значения переменной w, отвечающей за ширину импульса, и переменной s, отвечающей за скошенность. В зависимости от того, положительное или отрицательное значение присвоено переменной s, будет определено, какой фронт будет скошен в той или иной степени, в зависимости от значения переменной. На рисунке 17 переменная s имеет значение 1, следовательно его задний фронт скошен в максимальной степени (область значений переменной s -1 <s <1). Тогда как присвоение переменной s отрицательного значения (рисунок 18) приведет к изменению переднего фронта импульса.
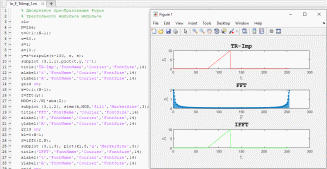
Рисунок 17. Изменение ширины и скошенности заднего фронта импульса
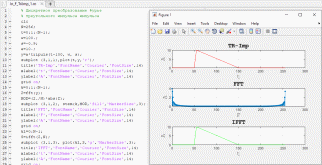
Рисунок 18. Изменение скошенности переднего фронта импульса
Синусоида, модулированная функцией гаусса
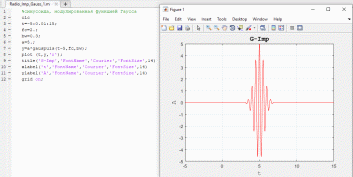
Рисунок 19. Синусоида, модулированная функцией гаусса
На рисунке 20 изображено изменение частоты и значения дробной полосы пропускания импульса (переменные fc и bw соответственно). Также на рисунке 21 изображено значительное уменьшение частоты сигнала, а также увеличение времени наблюдения до 150 (путем изменения предела вектора t).
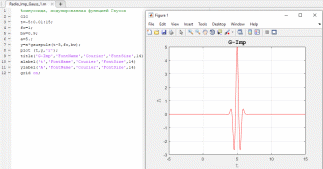
Рисунок 20. Изменение частоты и значения дробной полосы пропускания импульса
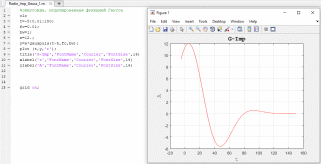
Рисунок 21. Уменьшение частоты импульса
Треугольный импульс
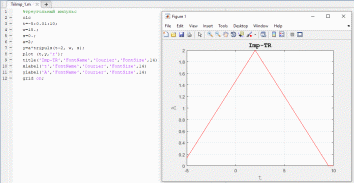
Рисунок 22. Треугольный импульс
На рисунке 22 изображен треугольный импульс. Переменная w отвечает за ширину импульса, a – за амплитуду, s – за скошенность переднего или заднего фронтов (в зависимости от знака). На рисунке 23 изображено изменение скошенности заднего фронта импульса путем изменения величины переменной s. Тогда как на рисунке 24 проиллюстрировано изменение обоих фронтов импульса с разными значениями s.
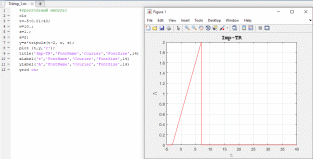
Рисунок 23. Изменение времени наблюдения и скошенности импульса
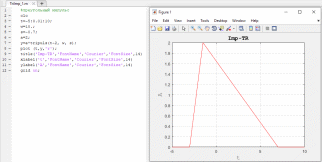
Рисунок 24. Изменение скошенности обоих фронтов импульса
