
лаб 6
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра «Информатика»
Лабораторная работа №6
«Основы нечеткой логики»
Выполнил: студент гр. БСТ21.
Вариант №13
Проверил: проф. Семин В.Г.
Москва, 2022 г.
Вариант задания по списку журнала группы |
Номер в задании 1 |
Номер в задании 2 |
Номер в задании 3 |
13 |
6 |
2 |
3 |
Задание 1. Нахождение основных характеристик нечеткого множества
Для заданного дискретного нечеткого множества А найти носитель, ядро, высоту, мощность, множества уровня (для заданных значений α). Указать, является ли данное множество нормальным. Если является субнормальным, преобразовать его к нормальному. Проверить является ли нормализованное множество унимодальным.
Вариант |
А |
α |
|
6 |
{0,1/3; 0,4/4; 0,8/5; 1/6; 0,6/7; 0,3/8} |
0,4 |
0,7 |
Решение:
1)Носитель
нечёткого множества А: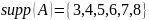
2)Ядро
нечеткого множества:
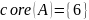
3)Высота
нечёткого множества:
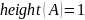
4)Мощность
нечёткого множества:
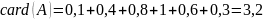
5)Множества
уровня нечёткого множества для α = 0,4:
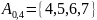
6)Множества
уровня нечёткого множества для α = 0,7:
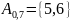
7)Данное множество является нормальным, так как высота равна 1
8) Данное множество является унимодальным, так как в заданном нечётком множестве µA(x) =1 только на одном х.
Задание 2. Операции над нечеткими множествами
2.1. Дано 3 нечетких множества A, B, C (заданы их функции принадлежности). Построить функцию принадлежности нечеткого множества D.
Вариант
2.
![]()
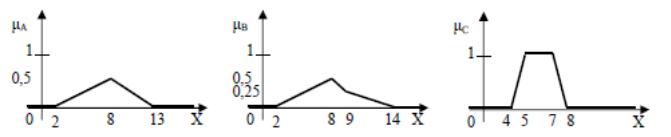
Решение:
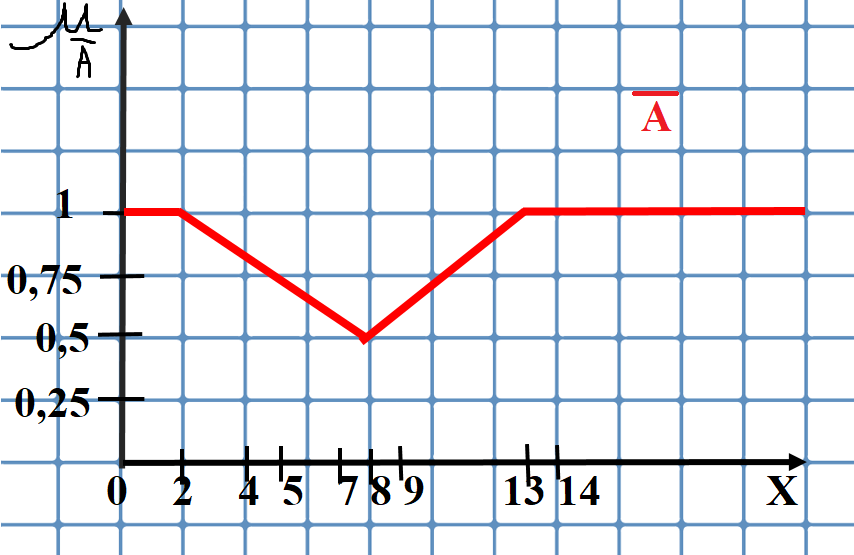
Рис.
1 – график функции принадлежности
нечеткого множества
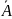
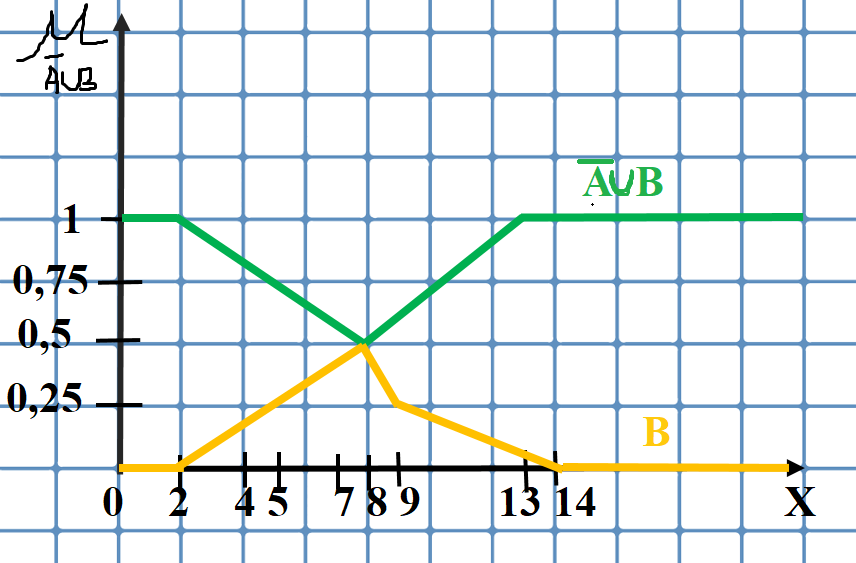
Рис.
2 – график функции принадлежности
нечеткого множества
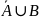
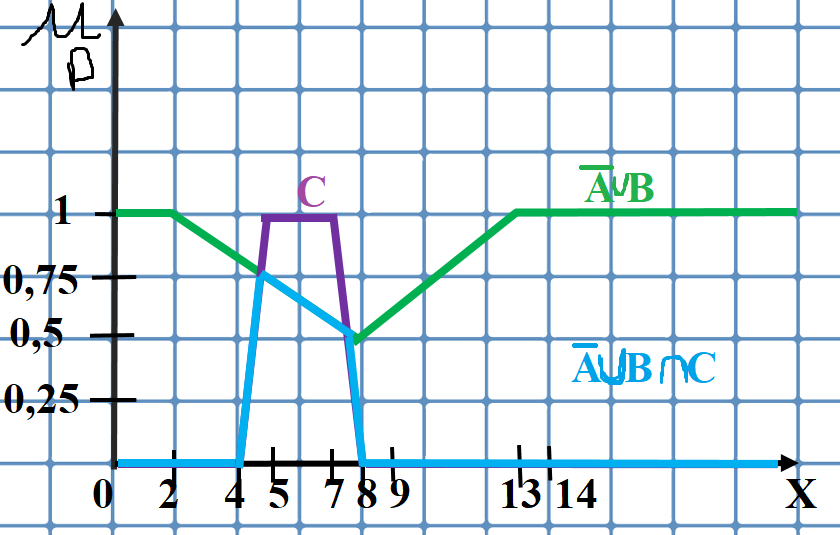
Рис.
3 – график функции принадлежности
нечеткого множества
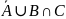
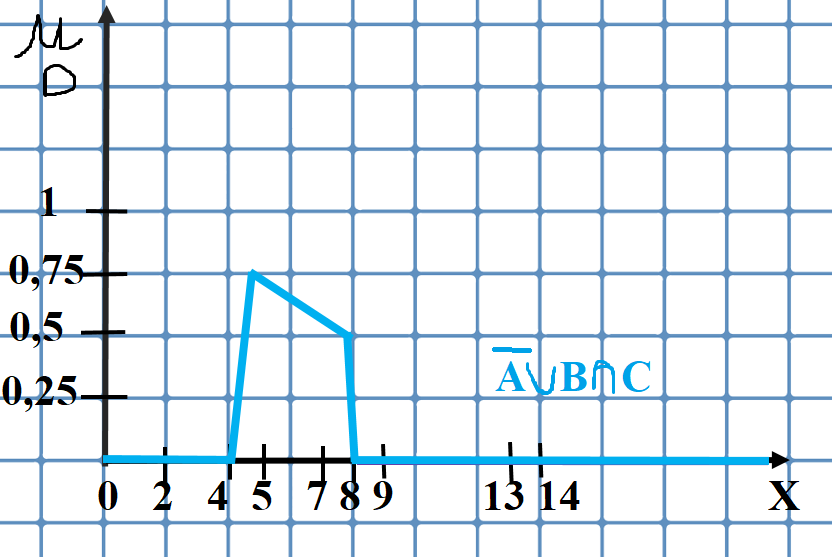
Рис. 4 – график функции принадлежности нечеткого множества D
Задание 3. Нечеткие множества А, В и С заданы таблично. Вычислить значение выражений .
№ 3 |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
х7 |
x8 |
A |
0,1 |
0,3 |
0 |
0,6 |
0,8 |
1 |
0,6 |
0,4 |
B |
0,9 |
0,8 |
0,3 |
0,1 |
0,2 |
0,4 |
0,6 |
0,4 |
C |
0,1 |
0,7 |
1 |
0,4 |
0,3 |
0,2 |
0,9 |
0 |
(B∩C)+A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
А = 0,1/х1 + 0,3/х2 + 0/х3 + 0,6/х4 + 0,8/х5 + 1/х6 + 0,6/х7 + 0,4/х8
B = 0,9/х1 + 0,8/х2 + 0,3/х3 + 0,1/х4 + 0,2/х5 + 0,4/х6 + 0,6/х7 + 0,4/х8
C = 0,1/х1 + 0,7/х2 + 1/х3 + 0,4/х4 + 0,3/х5 + 0,2/х6 + 0,9/х7 + 0/х8
![]()
(B∩C) = 0,1/х1 + 0,7/х2 + 0,3/х3 + 0,1/х4 + 0,2/х5 + 0,2/х6 + 0,6/х7 + 0/х8
![]()
(B∩C) +A = 0,19/x1 + 0,79/x2 + 0,3/x3 + 0,64/x4 + 0,84/x5 + 1/x6 + 0,84/x7 + 0,4/x8
(A∙B) = 0,09/х1 + 0,24/х2 + 0/х3 + 0,06/х4 + 0,16/х5 + 0,4/х6 + 0,36/х7 + 0,16/х8
![]()
(A∙B) ∪ С = 0,1/x1 + 0,7/x2 + 1/x3 + 0,4/x4 + 0,3/x5 + 0,4/x6 + 0,9/x7 + 0,16/x8
(B∩C)+A |
0,19 |
0,79 |
0,3 |
0,64 |
0,84 |
1 |
0,84 |
0,4 |
|
0,1 |
0,7 |
1 |
0,4 |
0,3 |
0,4 |
0,9 |
0,16 |
