21.3. Особенности расчетов предварительно напряженных конструкций по предельным состояниям второй группы

Расчет при действии изгибающих моментов и продольных сил. При расчете нормальных сечений по предельным состояниям второй группы в рамках общего деформационного метода следует рассматривать две стадии (рис. 21.3):

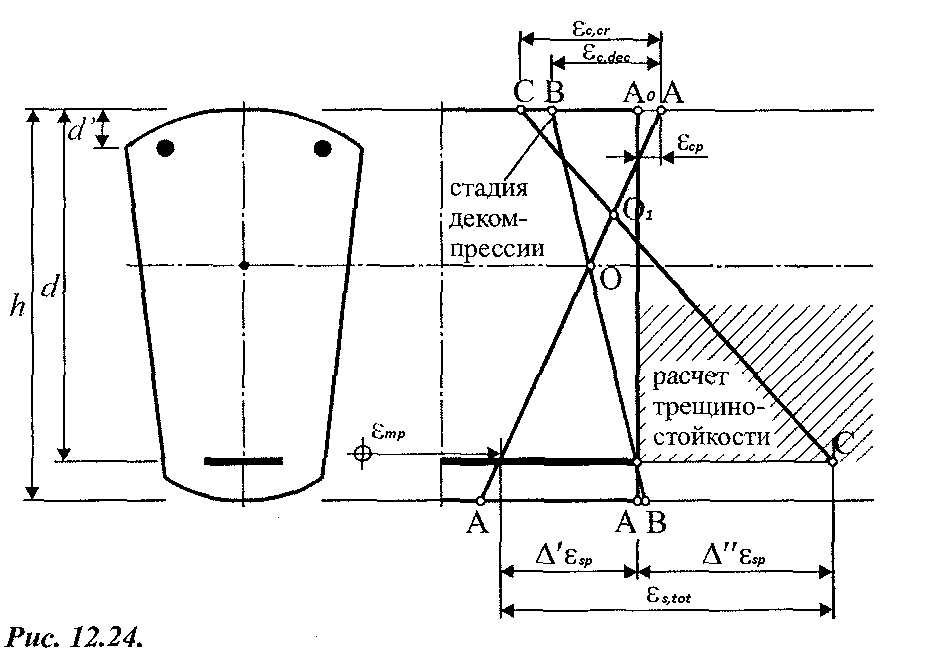
А–А – деформированное состояние после обжатия к моменту времени t;

В–В – стадия декомпрессии (напряжения в бетоне на уровне напрягаемой арматуры равны нулю);

С–С –деформированное состояние сечения с трещиной (расчет ширины раскрытия трещины производится на приращение относительной деформации )

Рис. 21.3. К расчету нормального сечения предварительно напряженной конструкции по предельным состояниям второй группы

• стадию декомпрессии (погашения начальных сжимающих напряжений в бетоне, на уровне центра тяжести напрягаемой арматуры, вызванных предварительным напряжением);

• стадию трещинообразования (после погашения начальных сжимающих напряжений в бетоне, вызванных предварительным напряжением).

В связи с этим вектор усилий, вызванных действием внешних нагрузок в расчетном сечении конструкции, в общем случае следует рассматривать как сумму:

(21.7)

(21.8)

(21.9)

где DN_Sd,1, DM_Sd,x1, DM_Sd,x2 – приращения усилий от внешней нагрузки, вызывающие погашение начальных сжимающих напряжений бетона, вызванных предварительным напряжением, на наиболее растянутой грани сечения, рассматриваемой на уровне центра тяжести напрягаемой арматуры;

DN_Sd,1, DM_Sd,x1, DM_Sd,x2 – приращения усилий от внешней нагрузки, приводящее к трещинообразованию сечения.

Расчет ширины раскрытия трещин. Расчетную ширину нормальных трещин w_k следует определять как для железобетонных элементов с тем, что среднее значение деформаций необходимо рассматривать как прирост деформаций в напрягаемой и ненапрягаемой арматуре от состояния соответствующего погашению начальных сжимающих напряжений в бетоне на уровне напрягаемой арматуры до состояния, соответствующего предельно допустимой ширине раскрытия трещин.

Среднее расстояние между трещинами для элемента, содержащего как напрягаемую, так и ненапрягаемую арматуру, определяют по формуле:

(21.10)

где Æ_si – диаметр ненапрягаемых стержней;

Æ_pj – диаметр напрягаемых стержней;

A_s – площадь мечения ненапрягаемой арматуры, располагаемой внутри эффективной площади растянутого бетона A_c,eff ;

k_s = 0,8 – для арматурных стержней периодического профиля;

k_s = 2,0 – для канатной арматуры;

n – общее количество стержней напрягаемой и ненапрягаемой арматуры.

 

Расчет прогибов. Прогибы предварительно напряженных элементов следует определять путем численного интегрирования средних значений параметров деформации по длине элемента с учетом исходного деформированного состояния сечений, имеющего место на стадии предварительного напряжения конструкции.

Средние значения параметров деформаций с учетом работы бетона с арматурой на участках между трещинами допускается определять по формуле:

(21.11)

где – вектор деформаций для элемента, работающего без трещин (на стадии декомпрессии);

– то же для элемента, работающего с трещинами в растянутой зоне;

При использовании упрощенного метода расчета по деформациям, прогибы предварительно напряженных конструкций допускается рассчитывать исходя из принципа суперпозиции, т.е. суммируя прогибы от внешних нагрузок и предварительного обжатия:

(21.12)

где M_Sd – расчетный момент, определенный для комбинации длительно действующих нагрузок;

N_pd = P_k,sup или P_k,inf;

a_k – коэффициент, зависящий от схемы приложения нагрузки;

a_р – коэффициент, зависящий от трассировки напрягаемого стержня (a = 1/8 – для стержней с прямолинейной осью трассы; a = 5/48 – для отгибаемых по параболе);

В(¥,t_o) – жесткость предварительно напряженного элемента.