
Кванты муравьев 1сем
.pdfпотенциальной энергии центробежной добавкой, а при r 0 |
имеет бесконечно высокую стенку. |
||
При этом |
поскольку центробежная добавка оказывается |
|
разной при разных l решения |
уравнения |
(5) — и функции (r) и собственные значения E |
— зависят от момента состояния, |
|
но не зависят от проекции момента, по которой, следовательно, имеется вырождение собственных значений. Дальнейший анализ уравнения (5) мы проведем на следующей лекции. А
на сегодня, до свидания.
3
Модуль 4: Трехмерное движение Лекция 4-3. Классификация состояний в центральном поле
Собственные значения и собственные функции оператора Гамильтона частицы в центральном
поле определяются из уравнения для функции (r) |
|
|
|
|
|
|
|
|
|
||
(r) |
2 |
|
|
2l(l 1) |
|
|
|
|
|
||
|
E U (r) |
|
|
|
|
|
(r) 0 |
|
|
(1) |
|
2 |
|
2 r |
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
которое совпадает с одномерным уравнением Шредингера |
|
для частицы, |
движущейся в |
||||||||
«одномерном» эффективном потенциале |
|
|
|
|
|
|
|
|
|
|
|
Uэфф (r) U (r) |
|
2l(l 1) |
|
|
|
|
|
(2) |
|||
|
2 r2 |
|
|
|
|
||||||
Эффективный потенциал определен при |
r 0 (поскольку только при таких |
r |
у нас определена |
||||||||
потенциальная энергия частицы). При |
r 0 |
уравнение (2) дополняется граничным условием: |
||||||||||||
(r 0) 0 |
, которое следует из условия конечности решения |
R(r) |
при |
r 0 |
. Такое граничное |
|||||||||
условие возникает в одномерной задаче, если эффективный |
|
|
|
|
|
|
||||||||
потенциал при |
r 0 имеет бесконечно высокую стенку. |
|
U |
|
|
|
||||||||
Добавка к потенциальной энергии, связанная с моментом |
|
|
|
|
|
|
||||||||
импульса |
в |
классической |
механике |
называется |
|
|
|
|
|
|
||||
центробежной |
энергией. Центробежная |
добавка |
к |
|
|
|
|
|
|
|||||
потенциалу является разной при разных |
l ; |
поэтому |
|
|
|
|
|
r |
||||||
|
|
|
|
|
|
|||||||||
уравнение (2) для состояний с разными моментами (а, |
|
|
|
|
|
|
||||||||
следовательно, |
и его |
решения — |
функции |
(r) |
и |
|
|
|
|
|
|
|||
собственные значения E ) является разным для разных |
|
|
|
|
|
|
|
|||||||
моментов и требует отдельного анализа для каждого |
U |
эфф,l 0 |
|
|
|
|
||||||||
|
|
|
|
|
||||||||||
момента. При этом от проекции момента уравнение не |
|
|
|
|
|
|
|
|||||||
зависит, |
поэтому имеет |
место |
вырождение |
|
|
|
|
|
|
|
||||
собственных значений |
гамильтониана |
по |
проекции |
|
|
|
|
|
|
r |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
момента (совпадение энергий у состояний с разными |
|
|
|
|
|
|
|
|||||||
проекциями). |
|
|
|
|
|
|
U |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для дальнейшего анализа уравнения (1) давайте |
|
min,l 0 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||
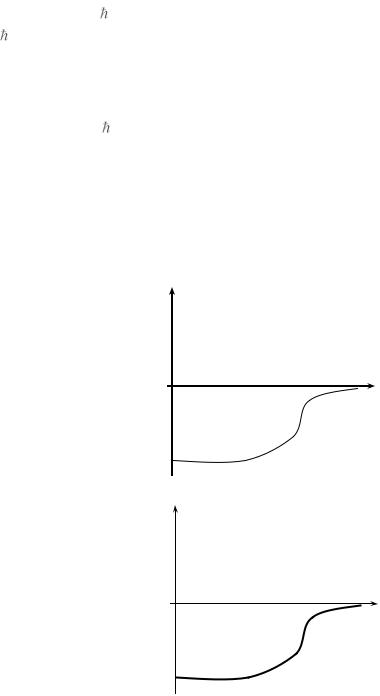
конкретизируем потенциал. Пусть потенциальная энергия U(r) представляет собой некоторую потенциальную яму (т. е. является энергией притяжения), такую, например, как это показано на
1
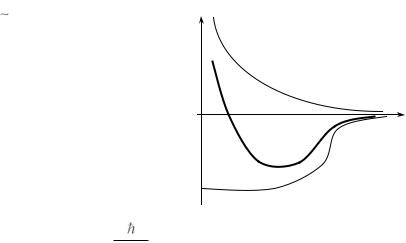
рисунке. Тогда для нахождения собственных значений и собственных функций гамильтониана с
моментом |
l 0 |
мы должны использовать уравнение (1) с эффективным потенциалом с |
l 0 |
(показан жирным на рисунке). Используя результаты нашего анализа одномерного уравнения Шредингера, заключаем, что есть набор собственных значений и собственных функций уравнения (1) с эффективным потенциалом с l 0 . Этот набор таков. При энергиях, меньших минимума потенциала (при E Umin,l 0 ) собственных значений нет. При энергиях, больших
Umin,l 0 , но меньших меньшего из граничных значений потенциала, могут существовать (а могут
и не существовать) дискретные собственные значения (уровни энергии), которым отвечает единственное хорошее решение уравнения (1). Для нумерации этих состояний введем квантовое
число nr , которое будем называть радиальным квантовым числом1. Радиальное квантовое число
нумерует дискретные собственные значения с l 0 в порядке возрастания их энергий En ,l 0 2. r
Точно так же и собственные функции (r) должны нести два индекса — n ,l 0 . Эти функции r
имеют свойства, аналогичные свойствам решений одномерного уравнения Шредингера. Для них справедлива осцилляционная теорема, они должны быть ортогональны, каждое собственное
значение невырождено. |
Число узлов функции n |
,l 0 |
|
(не считая нуль при |
r 0 ) равно nr 1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
(если для основного состояния |
nr |
1). Поскольку разные решения одномерного уравнения |
||||||||||||||||||
Шредингера ортогональны, ортогональны функции n |
,l 0 с разными |
nr |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n ,l 0 (r) n ,l 0 (r)dr |
n |
|
,n . |
|
|
|
|
|
|
U |
|
|
|
||||||
r |
|
r |
|
|
|
r |
|
r |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сколько состояний дискретного спектра с моментом |
l 0 |
|
|
|
|
|||||||||||||||
будут существовать, зависит от потенциальной энергии. |
|
|
|
|
|
|
||||||||||||||
Для нахождения |
собственных |
значений и |
собственных |
|
|
|
r |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функций гамильтониана |
с |
моментом |
l 1 |
|
нужно |
|
|
|
|
|||||||||||
использовать уравнение (1) с эффективным потенциалом с |
|
|
|
|
||||||||||||||||
l 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
||
|
|
|
|
|
|
U |
|
|
|
(r) U (r) |
|
|
|
|
|
|
||||
|
|
|
|
|
|
эфф |
2 r |
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
числа — n |
|
|
|||||||||||||
1 Надо сказать, что |
обозначение |
радиального |
квантового |
является |
довольно «корявым», но оно |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
является стандартным, поэтому и я его использую. |
|
|
|
|
|
|
|
|
|
|
||||||||||
2 Нумерацию самого радиального квантового числа можно начинать со значения |
|
n 1, а можно с n 0 . Все |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
r |
определяется соображениями удобства.
2

(см. рисунок, центробежная энергия показана пунктиром, эффективный потенциал — жирной линией). Далее используем наше понимание свойств собственных значений и собственных функций одномерной задачи. В этом потенциале будет своя система собственных значений
En |
,l 1 |
и собственных функций |
n |
,l 1(r) , которые мы будем отличать друг от друга радиальным |
r |
|
|
r |
|
квантовым числом nr , нумерация которого так же как и для состояний с моментом l |
0 , будет |
|||||||
начинаться от |
значения |
nr |
1. Таким образом, будет |
существовать |
система |
решений |
||
«одномерного» |
уравнения |
с |
моментом |
l 1, |
которой |
присущи все |
свойства |
решений |
одномерного |
уравнения — |
осцилляционная |
теорема, |
ортогональность, единственность |
||||
радиальной функции для каждого собственного значения и др. В частности, радиальная
волновая функция состояния с самой маленькой энергией (с моментом |
l 1) не имеет узлов, |
|||||||||
выполнено условие ортогональности разных решений этого уравнения |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n ,l 1 |
(r) |
n |
,l 1 |
(r)dr |
|
n |
,n |
|
|
r |
|
r |
|
|
|
r |
r |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
А вот радиальные функции, отвечающие разным моментам, не обязаны быть ортогональными — ведь они являются решениями разных уравнений. Ортогональность же разных собственных функций гамильтониана в этом случае обеспечивается ортогональностью сферических функций. Учитывая, что каждому собственному значению отвечает единственная
радиальная функция, кратность вырождения уровней с моментом l 1 |
равна 3, поскольку для |
|||||
каждой собственной энергии |
En |
,l 1 |
существуют три различных |
собственных |
функции, |
|
|
r |
|
|
|
|
|
отличающиеся проекцией момента на |
ось |
z — вторым индексом |
сферической |
функции, |
||
который для состояний с l 1 может принимать три значения m 1, 0, 1. |
|
|||||
И еще одной важной особенностью обладают собственные значения гамильтониана с
моментом |
l 1. Яма для состояний с моментом |
l 1 |
мельче ямы для состояний с моментом |
l 0 . А это значит, что энергии всех состояний с моментом l 1 больше энергий состояний с
моментом |
l 0 |
: для одного и того же квантового числа n |
выполнено условие E |
nr ,l 1 |
E |
nr ,l 0 |
. |
||||
|
|
|
|
|
r |
|
|
|
|||
Для нахождения собственных значений и собственных функций гамильтониана с |
|||||||||||
моментом |
l 2 |
нужно использовать уравнение (1) с эффективным потенциалом с l 2 |
|
|
|||||||
|
|
U |
|
(r) U (r) |
6 2 |
|
|
|
|
|
|
|
|
эфф |
2 r2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
(см. рисунок, центробежная энергия показана пунктиром, эффективный потенциал — жирной линией). В этом потенциале будет своя система собственных значений Enr ,l 2 и собственных
3
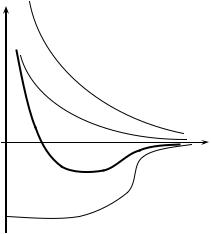
функций |
nr ,l 2 (r) , которые |
также |
пронумеруем радиальным квантовым числом nr , |
|||||
начинающимся со значения nr |
1 для состояния с самой маленькой энергии (среди состояний с |
|||||||
моментом l 2 . |
|
|
|
|
|
|
|
|
Поскольку эффективная потенциальная яма для |
U |
|||||||
|
||||||||
состояний с моментом l 2 мельче ямы для состояний с |
|
|||||||
моментом |
l 1, поэтому |
для собственных |
энергий |
|
||||
состояний с одним и тем же радиальным квантовым |
|
|||||||
числом выполнены условия |
En |
,l 2 |
En |
,l 1 . |
Каждое |
|
||
|
|
|
r |
|
r |
|
|
|
собственное значение с |
моментом |
l 2 |
является |
r |
||||
|
||||||||
пятикратно вырожденным из-за пяти возможностей для проекции момента m 2, 1, 0, 1, 2.
И далее решаем уравнение (1) для бóльших моментов l 3, 4,5,... Каждый раз мы будем получать все более и более мелкую яму, поскольку центробежная энергия, отвечающая бóльших моментов будет больше добавки для меньших моментов. Для каждого момента мы получим свое «одномерное» уравнение Шредингера, которое имеет свою систему собственных значений с данным моментом и радиальных функций. Эти решения мы перенумеруем радиальным квантовым числом nr , начиная с единицы.
На следующей лекции мы подведем итоги нашей классификации решений стационарного уравнения Шредингера для частицы в центральном поле и обсудим основные свойства собственных значений и собственных функций.
4
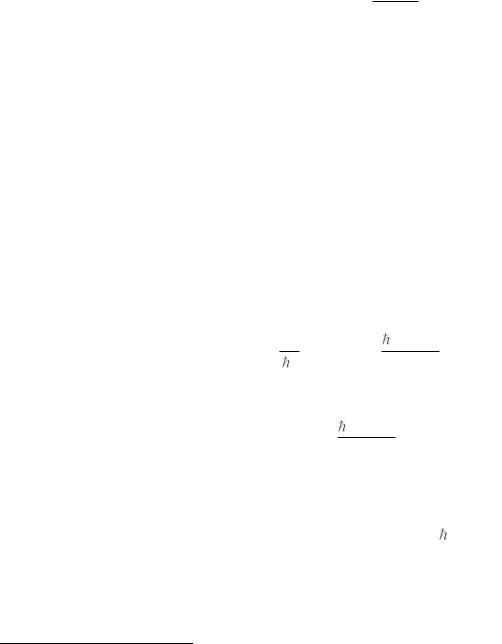
Модуль 4: Трехмерное движение Лекция 4-4. Классификация состояний в центральном поле (продолжение)
Повторю основные принципы решения уравнения Шредингера в центральном поле. Все собственные функции зависят от трех квантовых чисел — радиального квантового числа1,
момента импульса и его проекции на ось |
z |
f (r, , ) f |
|
|
(r, , ) |
|
n |
,l |
(r) |
Y |
( , ) |
|
|
|
|
||||||
|
|
|
|
|
r |
|
|
|
|
|
n |
,l ,m |
|
|
|
r |
|
lm |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Собственные энергии гамильтониана зависят от радиального квантового числа и момента, но не зависят от проекции. Поэтому все собственные значения (кроме значений с моментом l 0 )
вырождены с кратностью |
вырождения |
g 2l 1 — столько различных значений |
проекции |
|
момента существует для |
состояний с |
моментом |
l . Поэтому для перечисления |
энергий |
связанных состояний частицы в центральном поле нужны два квантовых числа — радиальное квантовое число и момент — nr и l :
E E |
,l |
n |
|
r |
|
Радиальные части волновых функций |
n |
,l (r) |
и собственные энергии |
En |
,l |
находятся из |
|
r |
|
|
r |
|
|
уравнения для радиальной волновой функции, которое оказывается разным для разных моментов и совпадает с одномерным уравнением Шредингера
|
|
2 |
|
|
|
|
2 |
l(l 1) |
|
|
||||
(r) |
E U (r) |
|
|
(r) 0 |
||||||||||
2 |
|
|
2 r |
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
в потенциале |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
l(l 1) |
|
|
|
|
|
|
||
|
|
|
|
|
|
, |
при r 0 |
|||||||
|
|
U (r) |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
Uэфф |
(r) |
|
|
2 r |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
при r 0 |
|||
|
|
, |
|
|
|
|
|
|
|
|||||
(1)
(2)
(отличие этих уравнений для разных моментов заключается в разных центробежных энергиях,
которые зависят от квадрата момента импульса состояния — |
2 |
1) ). Поэтому для каждого |
l(l |
||
уравнения (для каждого момента l ) получается своя система |
собственных значений и |
|
радиальных волновых функций, которые отличаются друг от друга радиальным квантовым числом, которое имеет тот же смысл, что и квантовое число в одномерной задаче (как для
1 Конечно, радиальное квантовое число можно ввести при условии существования дискретных собственных значений. В случае потенциала отталкивания или притяжения недостаточной величины таковых может не быть. В этом случае спектр решений уравнения Шредингера является непрерывным, а собственные функции зависят от непрерывного собственного значения E , дискретных момента l и проекции m , которые принимают все разрешенные для них значения.
1
потенциальной ямы или осциллятора) — номер состояния в порядке возрастания энергии. Для каждого момента радиальное квантовое число пробегает целые значения, начиная от nr 1 (для некоторых потенциалов оказывается удобным начинать отсчет радиального квантового числа от nr 0 ). При этом радиальные волновые функции (для каждого момента!) обладают такими же свойствами, что и волновые функции одномерной задачи — радиальные функции,
отличающиеся радиальными квантовыми числами, но с одинаковым моментом ортогональны,
радиальное квантовое число определяет число узлов радиальной волновой функции и т. д.
Из-за увеличения центробежной энергии с увеличением момента увеличиваются энергии всех дискретных связанных состояний с определенным моментом. Или для фиксированного
радиального квантового выполнено неравенство |
En ,l |
En |
,l , если l l |
|
. |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
Соотношение энергий |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
E |
|
|
|
|
|
E |
|
|
|
|
E |
|
|
|
||
дискретных |
собственных |
|
|
|
|
l 0 |
|
|
|
|
l 1 |
|
|
l 2 |
|
|
|
|
l 3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
4,l 2 |
|
|
E |
|
|
|
|
|
||
состояний |
частицы |
в |
En |
|
5,l 0 |
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
r |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3,l 3 |
|||||||||||||
|
|
|
|
|
|
|
|
r |
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
4,l 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
центральном |
поле |
можно |
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
2,l 3 |
||||
проиллюстрировать |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Enr 3,l 0 |
|
|
|
|
|
r |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
E |
|
4,l 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
графически |
на |
числовых |
|
|
n |
r |
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И т.д. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
n |
3,l 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,l 3 |
|
|
|||
осях, отвечающих |
разным |
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
n |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
n 2,l 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
E |
|
|
|
|
nr 2,l 1 |
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
моментам. |
Для |
|
этого |
r |
3,l 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
возьмем |
вертикальную |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1,l 2 |
|
|
|
|
|
|
|
|
|||||
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
r |
2,l 0 |
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
n |
|
|
n |
1,l 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
энергетическую |
ось, |
на |
E |
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
n |
|
1,l 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
которой будем |
черточками |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
откладывать |
энергии |
собственных состояний |
частицы с |
|
моментом |
l |
0 |
(конечно, эта |
||||||||||||||||||||||
иллюстрация носит качественный характер — точные значения энергий нужно получать, решая уравнение (1) для каждого момента, начиная с наименьшей). Будем на этой оси черточками
откладывать энергии собственных состояний с моментом |
l 0 |
(интервалы между состояниями |
и их количество для данного момента зависят от конкретного потенциала). Все эти энергии отвечают одному и тому же моменту, но разным радиальным квантовым числам. Правее нарисуем еще одну ось, на которой черточками отложим энергии состояний с моментом l 1.
Каждой такой черточке отвечает трехкратно вырожденное состояние дискретного спектра с моментом l 1. Еще правее нарисуем энергетическую ось, на которой будем откладывать энергии состояний с моментом l 2 (которые являются пятикратно вырожденными по проекции момента) и т. д. Отметим следующие характерные особенности этой картины.
2
1. Каждой черточке — уровню энергии — отвечает некоторое дискретное стационарное
состояние с определенным моментом. |
|
|
2. |
Каждый уровень энергии с моментом |
l 0 является вырожденным по проекции |
момента, |
кратность вырождения определяется соотношением g 2l 1 , причем все кратности |
|
вырождения нечетные числа. |
|
|
3. |
Черточки на более правых осях (с бóльшими моментами) начинаются с более высоких |
|
энергий, из-за увеличения центробежной энергии при увеличении момента состояния.
4.В свое время в атомной физике возникла терминология, которая широко используется
вквантовой механике, атомной и ядерной физике сегодня для обозначения состояний с
определенным моментом. Стационарные состояния с моментом l 0 называют |
s -состояниями, |
|||
состояния с моментом |
l 1 |
— |
p -состояниями, состояния с моментом l 2 — |
d -состояниями, |
состояния с моментом |
l 3 |
— |
f -состояниями и далее по порядку букв латинского алфавита. |
|
5. Радиальные волновые функции, отвечающие состояниям с одним и тем же моментом
(т. е. показанным на одной и той же оси) ортогональны.
6. Энергии состояний с разными моментами (черточки на разных осях) «ничего не знают» друг о друге, поскольку определяются из решений разных уравнений (с разными потенциалами). Поэтому энергии состояний с разными моментами, вообще говоря, разные. Не имеет места также ортогональность радиальных волновых функций для состояний с разными моментами.
7. Собственные функции, отвечающие разным собственным значениям, ортогональны.
Эта ортогональность обеспечивается ортогональностью сферических функций в случае разных моментов и ортогональностью радиальных волновых функций для разных собственных состояний с одним и тем же моментом.
8. Интервалы между уровнями энергии и их количество для данного момента зависят от конкретного вида потенциала. При небольших изменениях потенциала уровни энергии с каждым моментом должны смещаться по отношению к том положениям, которые показаны на рисунке, причем смещаться по-разному на разных осях. А это означает, что существуют такие потенциалы, для которых существует совпадение энергий состояний с разными моментами.
Поскольку дискретные собственные значения Enr ,l для разных значений l определяются из решения разных радиальных уравнений, то такое вырождение называют «случайным». Понятно,
однако, что точного совпадения двух абсолютно несвязанных величин быть не может (уж очень у нас много чисел на числовой оси!), поэтому существуют причины, почему именно для этих
3
потенциалов совпадают на первый взгляд несвязанные величины. Поэтому слова «случайное вырождение по моменту», как правило, берут в кавычки. Таким образом «случайным вырождением» называют совпадение энергий у состояний с разными моментами.
9. Кратность вырождения уровней при наличии случайного вырождения есть сумма кратностей вырождения по проекции момента тех состояний с разными моментами, энергии которых совпадают. Например, в кулоновском потенциале (для электрона в атоме водорода; см.
следующую лекцию) совпадают энергии второго состояния с |
l 0 и первого состояния с |
моментом l 1 (второго s-состояния и первого p-состояния). |
Кратность вырождения такого |
уровня равна 4 ( 2 0 1 2 1 1 4 ). |
|
4
Модуль 4: Трехмерное движение Лекция 4-5. Атом водорода
|
ˆ |
ˆ |
|
ˆ |
|
Найдем уровни энергии и общие собственные функции операторов |
H , |
2 |
и |
Lz |
. для |
L |
частицы массой и зарядом e , движущейся в кулоновском поле притяжения частицы с таким же по величине зарядом (электрон в атоме водорода)
|
e |
2 |
|
U (r) |
|
||
r |
|||
|
|||
Собственные функции перечисленных операторов имеют вид причем радиальные функции l (r) удовлетворяют уравнению
f (r, , )
( |
(r) / |
l |
|
r)Ylm
( ,
(1)
) ,
|
2 |
|
e |
2 |
|
2 |
l(l 1) |
|
|
|
||
(r) |
E |
|
|
|
|
(r) 0 |
||||||
2 |
|
|
|
|
|
2 |
|
|||||
l |
|
r |
|
2 r |
l |
|
||||||
|
|
|
|
|
|
|
|
|
||||
(2)
и граничному условию |
l (r 0) 0 |
. Поскольку потенциал обращается в нуль при |
r , |
состояния дискретного спектра — связанные состояния электрона в атоме — имеют энергии,
меньшие нуля. Поэтому будем решать уравнение (2) для отрицательных энергий.
Введем безразмерную координату |
r |
|
r / a , где |
a |
2 |
/ me |
2 |
— величина, имеющая |
|
||||||||
|
|
|
размерность длины и называемая боровским радиусом атома (в дальнейшем для упрощения записи формул штрих у безразмерной координаты опущен). В новых переменных уравнение (2)
имеет вид
|
d 2 |
|
2 |
|
l(l 1) |
|
|
|
|||
|
|
|
2 |
|
|
|
|
|
|
l (r) 0 |
(3) |
|
2 |
r |
r |
2 |
|||||||
dr |
|
|
|
|
|
|
|
|
|||
где 2 2E /(e2 / a) — безразмерное собственное значение энергии (которое для состояний
дискретного спектра является положительным). Собственное значение |
|
2 |
будем искать из |
|
условия существования «хороших» решений уравнения (3). Для этого будем решать уравнение
для произвольного положительного параметра |
2 |
, а потом проведем исследование зависимости |
|
||
решений от этого параметра — те значения |
|
2 , при которых существуют конечные и |
непрерывные решения уравнения (3) при всех значениях r ( 0 r ) определяют дискретные собственные значения для каждого момента l .
Решаем сначала уравнение (3) на асимптотиках — r 0 и r . При r 0 уравнение
(3) дает
1
