ЧМ_2023

1. Приближенные числа. Абсолютная и относительная погрешности. Значащие и верные цифры числа.

Кточным относятся числа, которые дают истинное значение исследуемой величины.

Кприближенным относятся числа, близкие к истинному значению, причем степень близости определяется погрешностью вычислений. Это связано с тем, что при измерениях появление приближенных чисел связано с несовершенством измерительных приборов. Кроме того, часто нет необходимости знать точное значение интересующей величины.

Пусть x - точное значение числа, а X - его приближение. Тогда X есть приближенное значение числа x с недостатком, если X < x , и приближенное значение с избытком, если x < X . Число x будет для самого себя приближением одновременно с недостатком и с избытком.

Если x - точное, неизвестное значение некоторой величины, а X - его приближение, то разность x - X называется ошибкой, или погрешностью приближения. Часто знак ошибки x - X неизвестен, поэтому используется так называемая абсолютная погрешность приближенного числа x, определяемая равенством:

∆( ) = | − |, откуда имеем = ± ∆( )

Изучаемая числовая величина есть величина именованная, т.е. измеряется, например, в сантиметрах, килограммах и т.п. Погрешность имеет ту же размерность. Однако часто возникает необходимость заменить эту погрешность безразмерным числом - относительной погрешностью.

относительную погрешность часто выражают в процентах: δ( ) = ∆( ) · 100%

| |

Первая слева отличная от нуля цифра числа и все расположенные справа от нее, называются значащими.

Цифра числа, записанного в десятичной системе, называется верной, если если абсолютная погрешность числа х не превосходит одной единицы соответствующего разряда десятичного числа. Цифры, не являющиеся верными, называются сомнительными. Если верная цифра - значащая, то она называется верной значащей цифрой.

Вид записи приближенного числа должен показывать его абсолютную погрешность, которая не должна превосходить единицы последнего разряда, сохраняемого при записи. Другими словами, приближенные числа принято записывать таким образом, чтобы все цифры числа, кроме нулей впереди, если они есть, были значащими и верными цифрами.

1

2. Погрешности арифметических операций - погрешности суммы, разности, произведения, частного приближенных чисел. Погрешность вычисления функции одной и многих переменных.

Пусть x и y – точные числа, и – их приближения, ∆( ) и ∆( ) – их абсолютные, а δ( ) и δ( )

– их относительные погрешности соответственно.

Погрешность суммы и разности.

∆( + ) ≤ ∆( ) + ∆( ), т.е. абсолютная погрешность суммы не превосходит суммы их абсолютных погрешностей

∆( − ) ≤ ∆( ) + ∆( ), аналогично для разности

∆( 1 + 2 + ... + ) ≤ ∆( 1) + ∆( 2) + ... + ∆( )

Из полученных результатов, вытекают следующие правила сложения:

1)выделяются числа, имеющие наибольшую абсолютную погрешность

2)более точные числа округляются таким образом, чтобы сохранить в них на один знак больше, чем в выделенном числе

3)производится сложение или вычитание всех чисел с учетом сохраненных знаков

4)полученный результат округляется на один знак

Относительная погрешность суммы и разности определяются соотношениями:

Погрешность произведения.

∆( · ) ≤ | |∆( ) + | |∆( ) + ∆( )∆( ), из чего можно получить правила умножения:

1)выделяется число с наименьшим количеством верных значащих цифр

2)оставшиеся сомножители округляются таким образом, чтобы они содержали на одну значащую цифру больше, чем количество верных значащих цифр в выделенном числе

3)в произведении сохраняется столько значащих цифр, сколько верных значащих цифр имеет выделенное число

δ( · ) = ∆( · ) = δ( ) + δ( ) + δ( ) · δ( )

| · |

Погрешность частного.

1) выделяется число с наименьшим количеством верных значащих цифр

2

2)оставшиеся числа округляются таким образом, чтобы они содержали на одну значащую цифру больше, чем выделенное число

3)в полученном результате деления сохраняется столько значащих цифр, сколько верных значащих цифр имеет выделенное число.

На практике при работе с числами достаточно хорошей точности обычно считают, что

∆( ) · ∆( ) ≈ 0, δ( ) · δ( ) ≈ 0, 1 − δ( ) ≈ 1. Поэтому вместо вышеперечисленных формул, пользуются следующими:

3. Представление чисел в ЭВМ. Понятия машинного эпсилон, машинной бесконечности, машинного нуля.

Целые числа, представимые в ЭВМ (целые машинные числа) - это все целые числа, принадлежащие замкнутому интервалу [-N, N]. В языке Паскаль, например - это числа диапазона [-32768, 32767]. Арифметические операции с целыми машинными числами выполняются на ЭВМ точно, если результат принадлежит интервалу. В противном случае фиксируется ошибочная ситуация, а результат операции не определен или не имеет смысла.

Вещественные числа могут быть записаны в двух формах. Обычную форму записи числа в виде: =± −1... 1 0, −1 −2... − , называют записью с фиксированной запятой. В

примера, не является однозначной. Для устранения этой неоднозначности принято первый множитель брать меньше единицы, и он должен состоять только из значащих цифр. Такая

форма записи числа называется нормализованной – = · β , здесь p - целое число, называемое порядком числа x, m - число с фиксированной запятой, называемое мантиссой числа x. Первая после запятой цифра числа m всегда отлична от нуля.

Для записи вещественных чисел в ЭВМ отводится фиксированное число разрядов (разрядная сетка), в которой выделены разряды для записи мантиссы, порядка, знаков мантиссы и порядка. Таким образом, множество машинных вещественных чисел характеризуется следующими четырьмя целыми константами: основанием счисления β, β >2,

3

точностью t, нижней границей экспоненты − и верхней границей экспоненты +. Ненулевые машинные вещественные числа имеют вид

Минимальное положительное число е которое может быть представлено в ЭВМ, называется

−

машинным нулем: ε0 = β −1. Максимальное положительное — машинной бесконечностью (

+

ε∞ = β (1 − β− )), т.е. машинные вещественные числа [− ε∞, ε∞]. Число ε1 = β− +1 называют

машинным эпсилоном. Оно зависит от разрядности мантиссы и характеризует точность представления чисел.

4. Вычислительные задачи. Корректность и обусловленность вычислительных задач.

Обусловленность и корректность постановки задачи.

Пусть в результате решения задачи по исходному значению величины x находится значение искомой величины y. Если исходная величина имеет абсолютную погрешность ∆( ), то решение y имеет абсолютную погрешность ∆( ). Задача называется обусловленной по исходному параметру x, если решение y непрерывно зависит от x. Другими словами, малые погрешности в исходном величине приводят к малым погрешностям в результате расчётов.

Задача называется поставленной корректно, если для любых значений исходных данных её решение существует, единственно и обусловлено по исходным данным. Отсутствие обусловленности означает, что даже незначительные погрешности в исходных данных приводят к большим погрешностям в решении или вовсе к неверному результату.

5. Прямая и обратная задачи теории погрешностей.

Для оценки влияния погрешностей округления на результат вычислений по некоторому алгоритму (прямая задача теории погрешностей), предполагают, что этот результат является действительной функцией от входных параметров: = ( 1, 2, ..., ). Поскольку входные

данные 1, 2, ..., не точные, то = ( 1, 2, ..., ) - приближенное значение результата.

Если = ( 1, 2, ..., ) – непрерывно дифференцируемая функция своих аргументов, то по формуле конечных приращений Лагранжа имеем следующую оценку погрешности:

Здесь точка (θ1, θ2,..., θ ) расположена между ( 1, 2,..., ) и ( 1, 2,..., ).

4

Оценка показывает, что накопление погрешностей округления зависит от величины входных параметров и от характера алгоритма.

относительных погрешностей входных данных. Если значения всех коэффициентов усиления ограничены по абсолютной величине единицей, то накопления погрешностей не происходит. Коэффициенты часто называют числами обусловленности задачи.

При анализе погрешностей возникают две задачи:

1)прямая – зная точность исходных данных оценить точность полученного результата

2)обратная - определить точность, с которой необходимо задавать исходную

информацию, чтобы обеспечить требуемую точность решения Для случая дифференцируемой функции одной переменной грубое решение обратной задачи

Для функций большего числа переменных обратная задача некорректна. Для ее решения необходимы дополнительные условия.

6. Прямые методы решения систем линейных алгебраических уравнений. Метод Гаусса: основная идея и схемы реализации (схема единственного деления и схемы с выбором главных элементов).

Прямые методы используют конечные соотношения и формулы для вычисления неизвестных. К прямым (или точным) методам решения СЛАУ относятся алгоритмы, которые в предположении, что вычисления ведутся без округлений, позволяют получить точное решение системы за конечное число арифметических действий. В прямых методах число необходимых для решения арифметических операций зависит только от вида вычислительной схемы и от порядка матрицы n.

Большинство прямых методов основано на идее последовательного эквивалентного преобразования заданной системы с целью исключения неизвестных из части уравнений. В результате исходная система преобразуется в эквивалентную ей систему с матрицей более простой формы.

В основе методов лежит следующее утверждение: пусть все главные миноры матрицы А отличны от нуля, тогда существуют такие нижняя L и верхняя U треугольные матрицы, что матрица A представима в виде произведения этих матриц: A = LU. Если все элементы диагонали одной из такой треугольных матриц фиксированы (ненулевые), то такое разложение единственно.

Метод Гаусса (схема единственного деления). Основная идея метода состоит в том, что система приводится к эквивалентной ей системе с верхней и треугольной матрицей и единичной диагональю (прямой ход исключения). Из полученной системы последовательно, начиная с последнего уравнения находятся неизвестные (обратный ход исключения).

5

Метод Гаусса (с выбором главного элемента). Метод заключается в том, что при прямом ходе в алгоритме метода Гаусса на каждом шаге исключения производится выбор наибольшего по модулю элемента в качестве ведущего. Этого достигают перестановкой строк и столбцов матрицы коэффициентов. Наиболее распространенной в вычислительной практике является стратегия выборов главного элемента столбца - нахождение максимального по модулю элемента k-ого столбца матрицы и использование его в качестве ведущего элемента на k-ом шаге исключения. В этом случае для невырожденных систем гарантируется, что ведущие элементы не равны нулю и уменьшается погрешность при делении и последующем вычитании при преобразованиях.

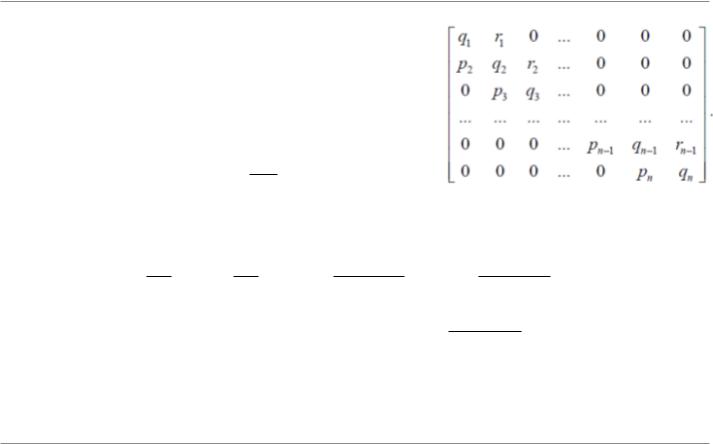
7. Метод прогонки решения систем линейных алгебраических уравнений с трехдиагональной матрицей.

Этот метод является модификацией метода Гаусса для систем специального вида с трехдиагональной матрицей А, т.е. с матрицей, все элементы которой, не лежащие на главной и двух побочных диагоналях, равны нулю.

−1 + + +1 = , = 1, , 1 = 0, = 0.

Находя коэффициенты по рекуррентным формулам:

Обратный ход дает окончательное решение системы по формулам:

= , = +1 + , = − 1, 1

8. Обусловленность задачи решения систем линейных алгебраических уравнений. Нормы векторов и матриц. Число обусловленности.

Система уравнений считается плохо обусловленной, если малые изменения в коэффициентах матрицы или в правой части вызывают большие изменения в решении. Система уравнений считается хорошо обусловленной, если малые изменения в коэффициентах матрицы или в правой части вызывают малые изменения в решении.

Число обусловленности Cond(A) оценивает близость матрицы коэффициентов А к вырожденной.

1)Всегда ( ) ≥ 1

2)Если ( ) ≥ 1000 – матрица А плохо обусловлена.

3)Если 1 ≤ ( ) ≤ 100 – матрица А считается хорошо обусловленной.

6

( ) = || || · || −1||. Для оценки величины погрешностей и обусловленности систем используют нормы векторов и согласованные с ним нормы матриц.

Наиболее употребительными на практике являются следующие векторные нормы:

1) абсолютная векторная норма и 1-норма – || ||1 = ∑ | |.

=1

2) максимальная векторная норма или ∞-норма – || ||∞ = 1≤ ≤ | |

Согласованные с векторными соответствующие матричные нормы:

1) столбцовая матричная норма или 1-норма максимальная сумма модулей элементов

9. Приближенное решение систем линейных алгебраических уравнений итерационными методами. Необходимое и достаточное и достаточное условия сходимости итерационного метода.

К итерационным (или приближенным) методам относятся методы, которые даже в предположении, что вычисления ведутся без округлений, позволяют получить решение системы лишь с заданной точностью. Итерационные методы применяются для решения систем высокого порядка. К ним относятся методы:

1)Метод Якоби (метод простой итерации)

2)Метод Зейделя

3)Метод релаксации

4)Метод скорейшего спуска

5)Метод минимальных поправок

Для решения итерационным методом система линейных алгебраических уравнений из вида= должна быть приведена к виду = + , где G – некоторая матрица, f - преобразованный вектор свободных членов.

Затем выбирается начальное приближение - некоторый произвольный вектор ( ) – и по

формуле ( ) = ( −1) + строится рекуррентная последовательность векторов

{ (1), (2), ..., ( ), ...}.

Для сходимости этой последовательности при любом начальном приближении необходимо и достаточно, чтобы все собственные значения матрицы G были по абсолютное величине меньше единицы.

7

10. Итерационные методы решения систем линейных алгебраических уравнений: условия завершения итерационного процесса.

Для окончания итерационного процесса на практике используют три способа:

При первом определяют величину стабилизации и прекращают вычисления, если она меньше ε, т. .е.:

|| ( +1)−( )||

{|| ( +1)||, || ( )||} ≤ ε.

Недостатком этого способа является то, что при медленно сходящихся итерациях величина стабилизации может быть малой, хотя приближенное решение сильно отличается от точного.

При втором способе вычисляют нормы невязки до начала итерация (для начального приближения) и на каждой итерации. Итерации прекращаются при выполнении неравенства:

|| ( )−|| || (0)−|| ≤ ε

При третьем способе предварительно оценивается число итераций, необходимое для получения заданной точности ε. Если для погрешности итерационного метода выполняются оценки || ( ) − || ≤ || (0) − ||, где (0, 1), то говорят, что метод сходится со скоростью геометрической прогрессии со знаменателем q. Тогда, зная величину q, можно

определить число итераций n, решив неравенство < ε.

11. Метод Якоби и метод Зейделя решения систем линейных алгебраических уравнений.

Два классических итерационных метода – метод Якоби и метод Зейделя. Оба используют преобразованную систему

Метод Якоби использует следующий алгоритм построения приближений:

сходится при любом начальном приближении.

8

Модификация метода Якоби, в которой при k-ой итерации вычисления следующего ()

и приводит, как правило, к ускорению сходимости.

Приведенные выше методы Якоби и Зейделя относятся к одношаговым итерационным методам – для нахождения ( +1) требуется помнить только одну предыдущую итерацию.

12. Функции MATHEMATICA, используемые для работы с векторами, матрицами и системами линейных алгебраических уравнений: Dot[….], LinearSolve[….], Inverse[…], Det[….], Norm[…], MatrixForm[…]…

1)Dot[...] – операция произведения матриц, векторов, также можно задать с помощью точки.

2)Inverse[A] – вычисляет обратную матрицу −1 для квадратной матрицы A.

3)MatrixForm[{a, b}, {c, d}] – выводит матрицу в традиционном виде.

4)Det[A] – вычисляет определитель матрицы A.

5)Norm[A] – вычисляет норму (длину) вектора/матрицы A.

6)LinearSolve[A, B] – находит решение X для матричного уравнения · =

13. Постановка задачи интерполирования функции. Существование и единственность интерполяционного многочлена.

Задача интерполирования состоит в том, чтобы по значениям функции ( ) в нескольких точках отрезка восстановить ее значения в остальных точках этого отрезка. Такая задача допускает сколь угодно много решений. Задача интерполирования возникает, например, в том случае, когда известны результаты измерения = ( ) некоторой физической

величины ( ) в точках , = 0, 1, ..., и требуется определить ее значения в других точках.

Интерполирование используется также при сгущении таблиц, когда вычисление значений х трудоемко. Иногда возникает необходимость приближенной замены или аппроксимации данной функции другими функциями, которые легче вычислить.

Теорема существования и единственности интерполяционного обобщенного многочлена: для того чтобы для любой функции при любых наборах попарно неравных узлов существовал интерполяционный обобщенный многочлен необходимо и достаточно, чтобы эта система функций была системой Чебышева на отрезке [a; b]. При этом интерполяционный обобщенный многочлен будет единственным.

9

14. Интерполяционная формула Лагранжа. Погрешность интерполяционной формулы.

( − 0)...( − −1)( − +1)...( − )

( ) = ∑ ( ) ( − )...( − )( − )...( − ) =

=0 0 −1 +1

Недостатком формы Лагранжа интерполяционного многочлена является то, что при добавлении новых узлов интерполяционный многочлен надо строить заново. Но он удобен при одновременном интерполировании нескольких функций, заданных в одних и тех же узлах, т.к. коэффициенты одинаковы для всех функций и зависят только от узлов:

Погрешность интерполяции методом Лагранжа зависит от свойств функции, от расположения узлов интерполяции и точки x. Полином Лагранжа имеет малую погрешность при небольших значениях n (n<20). При больших n погрешность начинает расти, что свидетельствует о том, что метод Лагранжа не сходится (то есть его погрешность не убывает с ростом n).

15. Интерполяционные формулы Ньютона для интерполирования в начале и конце таблицы. Погрешность интерполяционных формул.

Часто интерполирование ведется для функций, заданных равномерными сетками, т.е. шаг таблицы = +1 − постоянен. Ограничимся рассмотрением интерполяционных формул

Ньютона для этого случая. Введем понятие конечных разностей. Пусть функция задана таблицей с постоянным шагом. Разности между значениями функции в соседних узлах называются конечными разностями первого порядка: ∆ = +1 − , = 0... − 1. Из

конечных разностей первого порядка можно получить конечные разности второго порядка:

∆2 = ∆ +1 − ∆ , = 0... − 2 – это разность между двумя соседними разностями

первого порядка. Конечные разности третьего порядка: ∆3 = ∆2 +1 − ∆2 , = 0... − 3

Первая интерполяционная формула Ньютона:

10