4. Процесс распространения волн в длинной линии

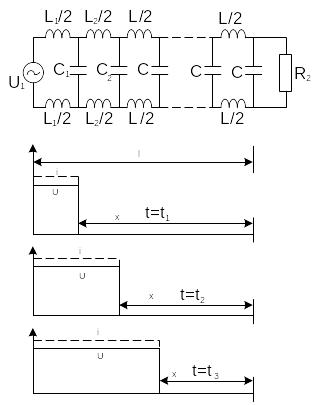
На рисунке l – длина линии, x – координата, отсчитываемая от конца линии.

Пусть линия питается от источника постоянного напряжения U. К моменту времени t1 емкость 1-го элементарного участка C1 зарядится через индуктивность L1/2 до напряжения U. К моменту времени t2 емкость 2-го элементарного участка С2 зарядится от емкости С1 через индуктивность L2/2 до того же напряжения, а источник полностью восстановит заряд емкости С1. Таким образом, происходит передача энергии в каждый следующий элементарный участок электрической цепи. Такой процесс последовательного заряда элементарных емкостей через элементарные индуктивности создает волну тока и напряжения, движущуюся от источника к концу линии. Эту волну называют падающей. Если нагрузка в конце линии поглощает энергию падающей волны не полностью, то возникает обратная или отраженная волна тока и напряжения, процесс распространения которой аналогичен распространению падающей волны. Таким образом, в каждом сечении линии одновременно существуют 2 волны – падающая и отраженная.

5. Телеграфные уравнения. Режимы работы длинной линии. Режим бегущих волн.

Уравнения называются телеграфными, поскольку впервые были введены при исследовании процессов в телеграфных линиях. Уравнения позволяют установить изменения в линии с течением времени напряжения и тока в каком-либо сечении.

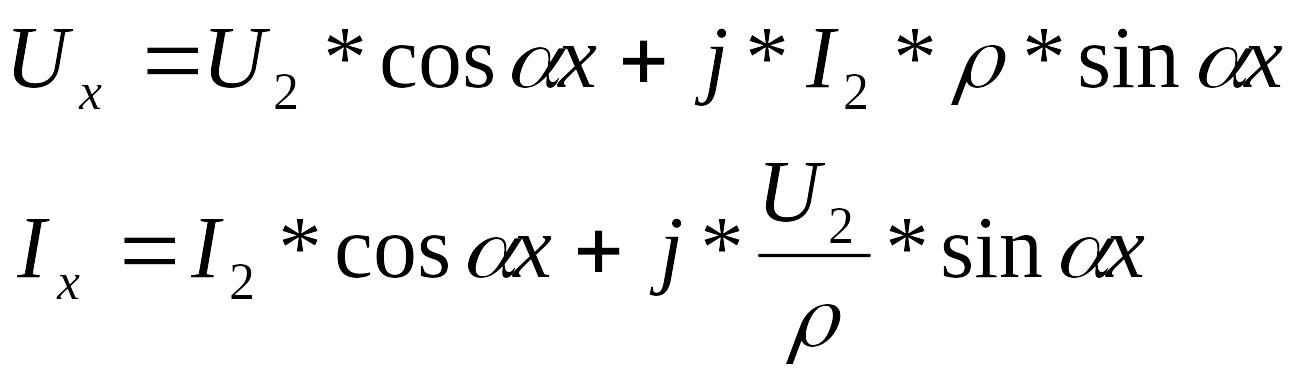
Уравнение позволяют найти значения напряжения и тока в любом сечении вдоль длинной линии. В этих выражениях:

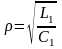- волновое сопротивление линии;

- фазовая постоянная, показывающая отставание фазы колебаний за время их распространения на единицу длины линии.

Полное приведение телеграфных уравнений из учебника:

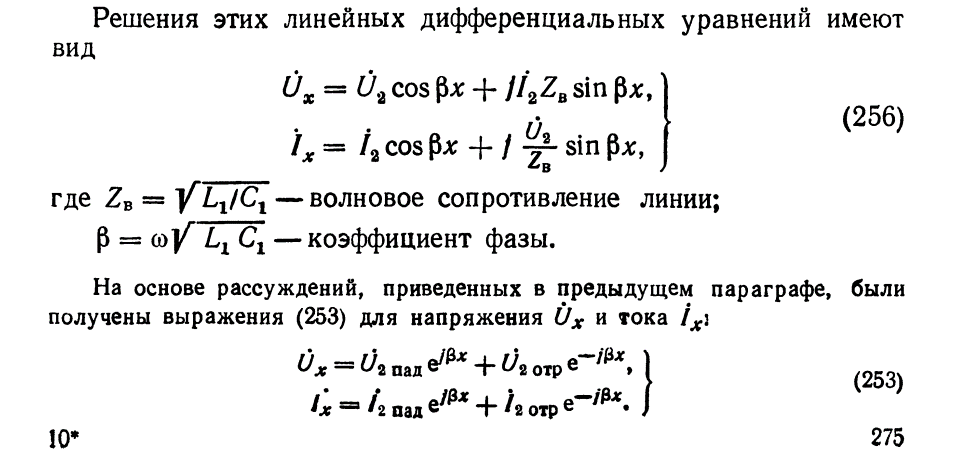
Формула 256 – телеграфные уравнения (лучше воспользоваться своим конспектом т.к. могут быть сложности с обозначениями (фазовая постоянная здесь бета, а не альфа, а волновое сопротивление Zв, а не ρ).

Режимы работы длинной линии

В зависимости от соотношения между волновым сопротивлением линии и сопротивлением нагрузки линии могут работать в режиме бегущих волн, стоячих волн или в режиме смешанных волн.

Бегущими волнами называются волны, фаза которых удаляется от источника возбуждения с постоянной скоростью, зависящей от свойств среды.

Стоячими волнами называют колебания, полученные в результате сложения двух бегущих волн, направленных навстречу друг к другу. Например, падающие и отраженные волны.

Режим бегущих волн

(лучший режим работы линии, вся энергия передается в нагрузку)

Бегущими волнами называют колебания, фаза которых удаляется от источника с постоянной скоростью, зависящей от свойств среды.

Бегущие волны в линии получаются в случае, если сопротивление нагрузки чисто активное и равно волновому сопротивлению линии. В этом случае:

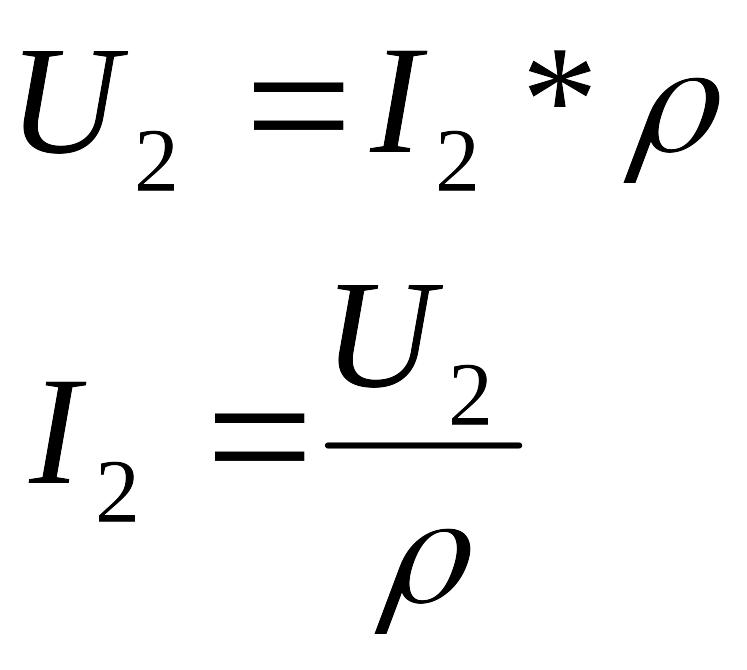
Мгновенные значения напряжения и тока в сечении линии с координатой х будут равны:

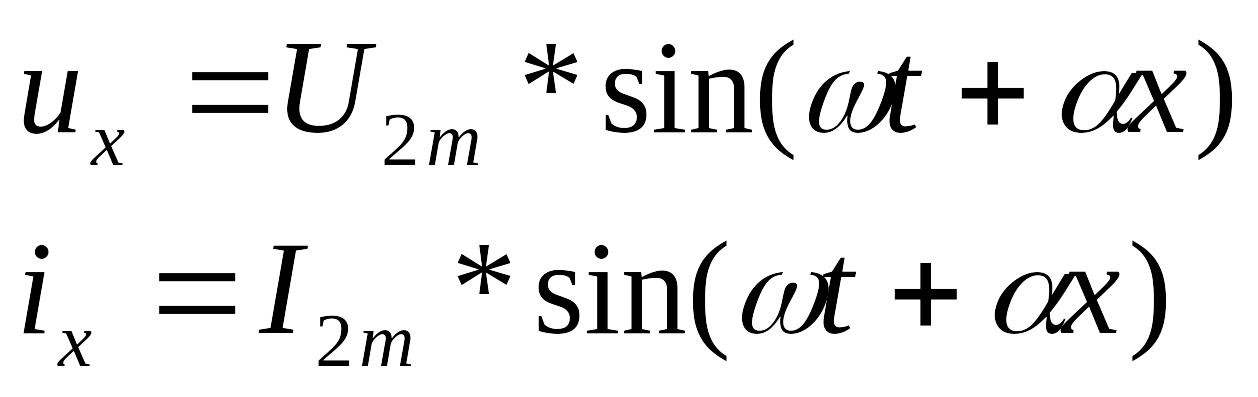
Скорость распространения бегущей волны тем меньше, чем больше погонные индуктивность и емкость:

Выводы:

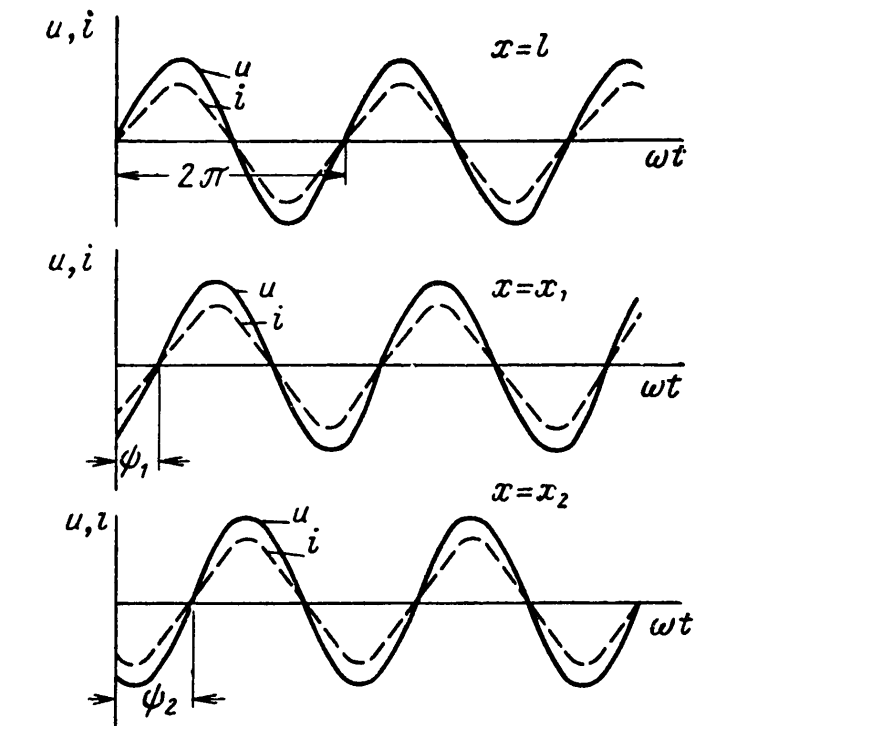
1) в каждом сечении линии напряжение и ток меняются синусоидально во времени;

2) амплитуды напряжения и тока не зависят от выбранной координаты х (линия без потерь), то есть постоянны по всей длине линии;

3) фазы напряжения и тока не изменяются;

4) сопротивление линии активно в любом сечении, т.к. в различных сечениях линии фазы U и I совпадают.

5) фазовая постоянная (α) может быть выражена через длину волны (λ), исходя из того, что при распространении бегущей волны на расстояние x=λ происходит отставание по фазе U или I на угол 2π, т.е. αx= λx=2π, откуда фазовая постоянная равна .

6) длина волны связана со скоростью распространения бегущих волн формулой:

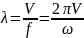
7) Волновое сопротивление линии — сопротивление, которая линия оказывает бегущей волне тока I в любом сечении линии.