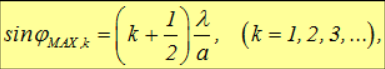Дифракция Френеля от диска и круглого отверстия. Пятно Пуассона. Дифракция в параллельных лучах от щели.

Дифракция на круглом отверстии

От источника S распространяется сферическая волна и встречает на своем пути экран с круглым отверстием. Картину наблюдаем в точке В, лежащей на прямой, соединяющей S с центром отверстия. Экран параллелен плоскости отверстия и находится от него на расстоянии b. Разобьем открытую часть волновой поверхности на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием.

Амплитуда результирующих колебаний в точке Р, возбуждаемая всеми зонами:

знак «+» соответствует нечетным m, «–» – четным m.

Если m нечетная, то А_рез в точке В будет больше, чем при свободном распространении волны, а если m – четное, то – меньше.

Если отверстие открывает одну зону Френеля, то в точке Р амплитуда А=А₁, т.е. вдвое больше, чем в отсутствии непрозрачного экрана с отверстием, а интенсивность света больше в 4 раза. Если отверстие открывает две зоны Френеля, то интенсивность в точке Р равна нулю.

Дифракционная картина от круглого отверстия вблизи точки Р имеет вид чередующихся темных и светлых колец с центрами в точке Р (если m – четное, то в точке Р темное кольцо, если m – нечетное, то в точке Р кольцо светлое).

Дифракция на диске

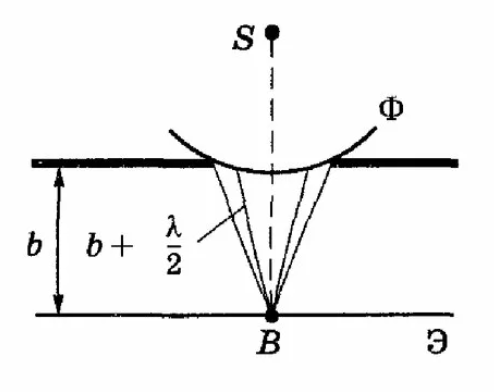
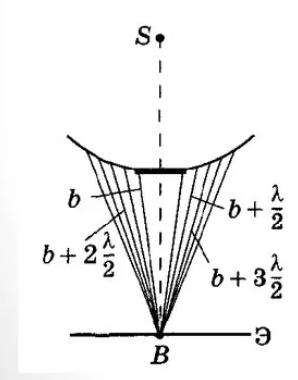
На пути сферической волны от источника S расположен круглый непрозрачный диск. Дифракционная картина наблюдается в точке В экрана Э, лежащей на линии, соединяющей S с центром диска. Экран параллелен диску. Зоны Френеля начинаем строить от краев диска.

Диск закрывает первые m зон Френеля:

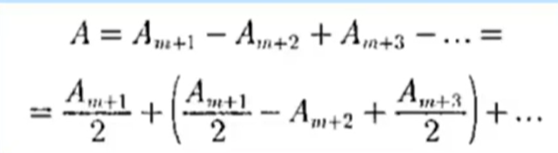
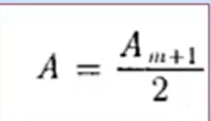
В точке В, в центре геометрической тени, всегда наблюдается интерференционный максимум, называемый пятном Пуассона, соответствующий половине действия только первой (m+1) открытой зоны Френеля и окруженный концентрическими с ним темными и светлыми кольцами.

По мере увеличения отношения диаметра d к расстоянию b яркость пятна Пуассона постепенно уменьшается, а следующее за ним темное кольцо расширяется, образуя область тени за диском.

Дифракция Френеля и Фраунгофера

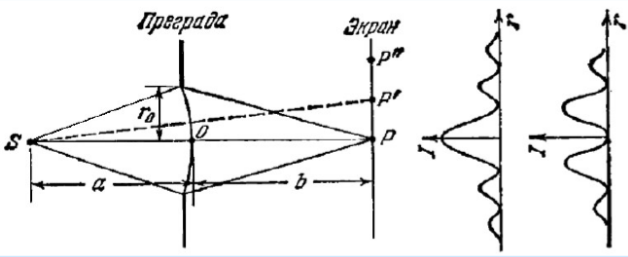
Различают два вида дифракции: Френеля и Фраунгофера. Если источник света S и точка наблюдения расположены от препятствия достаточно далеко: так, что лучи, идущие в точку Р, можно считать параллельными, говорят о дифракции Фраунгофера. В противном случае имеем дифракцию Френеля.

Дифракция на щели

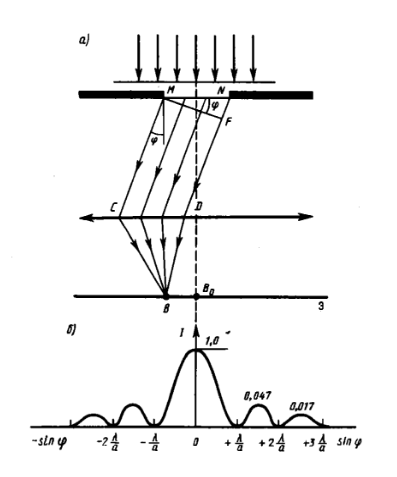Если размеры препятствия много меньше расстояния до источника, то волну, падающую на препятствие, можно считать плоской. Плоскую волну можно также получить, располагая источник света в фокусе собирающей линзы. На щель падает плоская волна. Для наблюдения дифракции за щелью нужно расположить собирающую линзу, в фокальной плоскости которой находится экран.

Линза сводит все падающие на нее под углом  параллельные лучи вместе на экране. Сама линза не вносит дополнительной разности хода.

Пусть плоская монохроматическая световая волна падает нормально плоскости щели шириной а. Оптическая разность хода между крайними лучами МС и ND, идущими от щели в произвольном направлении :

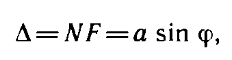
где F — основание перпендикуляра, опущенного из точки М на луч ND (волновая поверхность MF).

Зоны Шустера отличаются от зон Френеля тем, что их площадь уменьшается с ростом номера зоны (если вы помните, площади всех зон Френеля одинаковы). Границы зон Шустера выбираются таким образом, чтобы расстояние от конца последующей зоны до точки наблюдения было больше расстояния от конца предшествующей до точки наблюдения на половину длины волны

Если при наблюдении из точки В в щели помещается четное число зон Шустера (параллельных полос), то их вклады взаимно погасятся и в точке В будет наблюдаться минимум интенсивности света. Таким образом, уравнение:

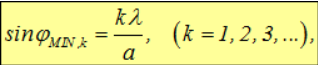
дает условие дифракционных минимумов.

Если при наблюдении из точки В в щели помещается нечетное число зон Шустера, то каждая зона гасит соседнюю, а оставшаяся последняя образует максимум. Поэтому условие максимумов имеет вид: