Расчет интерференционной картины от двух источников. Опыт Юнга. Интерференция света в тонких пленках.

В се источники света, кроме лазера, некогерентны, однако Юнг впервые пронаблюдал явление интерференции, разделив волну на две с помощью двух щелей. Юнг пошел на хитрость - на самом деле нет двух источников, есть один, только разделённый. Юнг получил когерентные источники делением волнового фронта.

d – расстояние между щелями

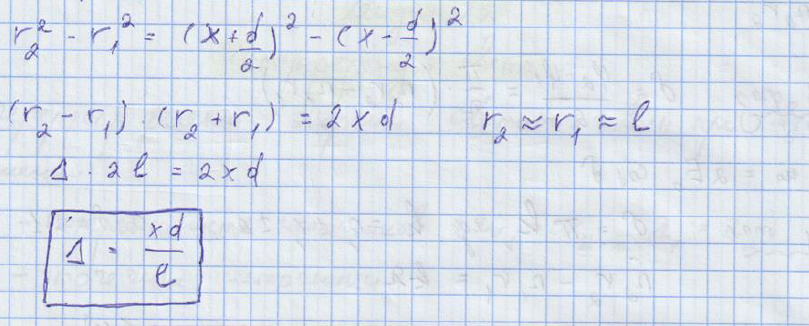
Интерференционные максимумы эквидистантные.

Интерференция в тонких плёнках

Результат интерференции двух волн: волны, отраженной от поверхности пленки, и волны, которая преломилась, а потом отразилась от нижней поверхности пленки. 

Волновая поверхность — геометрическое место точек, колеблющихся с одной и той же фазой.

При отражении от оптически более плотной среды происходит потеря полуволны.

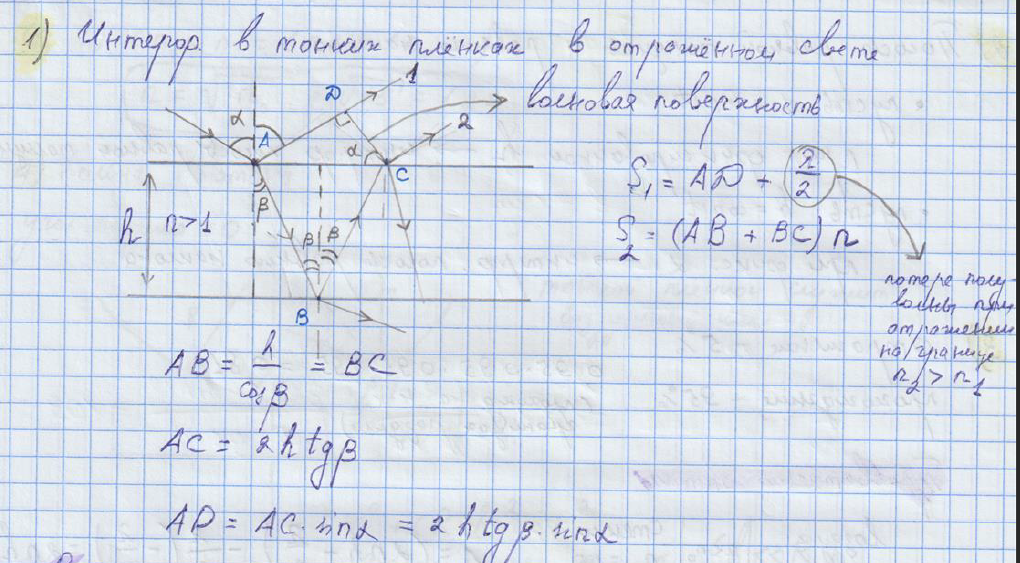
Чистая геометрия:

П ри больших k интерференционная картина размывается.

Интерференция света в тонких пленках. Полосы равной толщины и полосы равного наклона. Кольца Ньютона. Просветляющие покрытия.

Про интерференцию света в тонких плёнках написано в предыдущем вопросе.

Полосы равного наклона получаются при освещении пластинки постоянной толщины (h=const) рассеянным светом, в котором содержатся лучи разных направлений. Локализованы в бесконечности. Для их наблюдения используют собирающую линзу и экран, расположенный в фокальной плоскости линзы.

Полосы равной толщины наблюдаются при освещении пластинки переменной толщины (клина) (h не равно const) параллельным пучком света. Локализованы вблизи поверхности клина. Если свет падает на пластинку нормально, то полосы равной толщины локализуются на верхней поверхности клина.

Классическим примером полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной пластинки и плоско-выпуклой линзы с большим радиусом кривизны. Роль тонкой плёнки, от поверхности которой отражаются интерферирующие лучи, играет воздушный зазор (воздушный клин). При нормальном падении света полосы равной толщины имеют вид концентрических окружностей, а при наклонном падении – эллипсов.

Если луч падает нормально, то угол между ним и нормалью будет равен нулю.

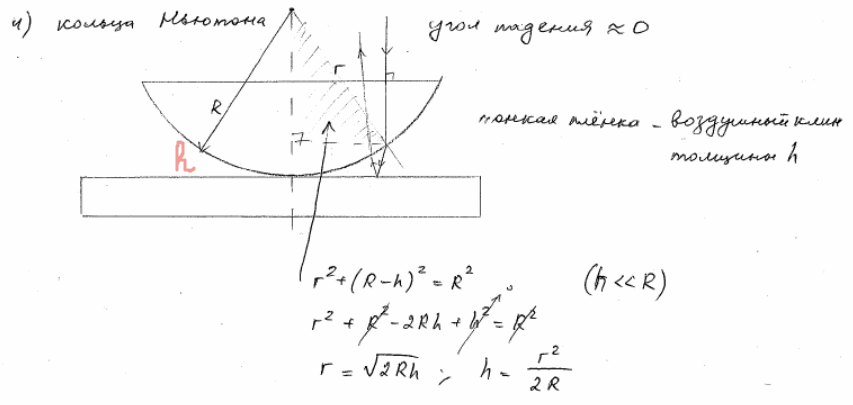
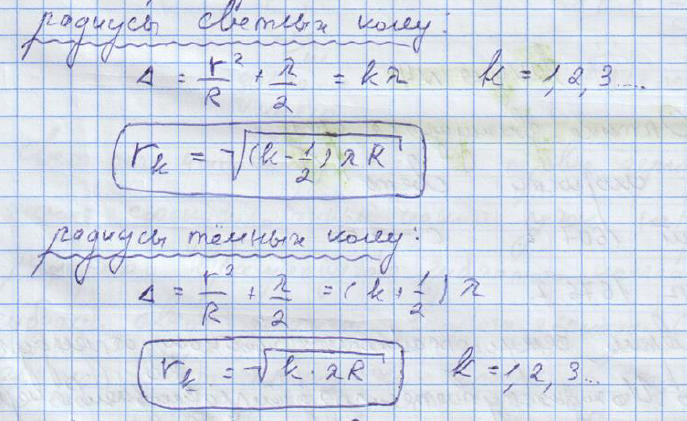
В проходящем свете явление потери полуволны наблюдаться не будет.

В проходящем свете в свете в центре светлое пятно (максимум), в отражённом – тёмное пятно (минимум).

Просветление оптики

Пусть на поверхность линзы падает свет с интенсивностью I₀, а отражается свет с интенсивностью I₀*r, где r – коэффициент отражения. Интенсивность прошедшего света I₀ - (I₀*r) = I₀*(1 – r).

Для двух поверхностей (а у обычной линзы их две) интенсивность прошедшего света:

I = I₀*(1 – r)²

Для k отражающий поверхностей интенсивность прошедшего света:

I = I₀*(1 – r)^k

Чтобы увеличить долю проходящего света и уменьшить долю отражённого на поверхность линзы наносится тонкий просветляющий слой (плёнку).

Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля.

Дифракция волн – огибание волнами препятствий.

Дифракция – общее явление для волновых процессов. Дифракция света обусловлена его волновой природой.

Дифракция света – явление отклонения света от прямолинейного направления распространения

при прохождении вблизи препятствий.

При определённых условиях свет может заходить в область геометрической тени.

Закон прямолинейного распространения света, законы отражения и преломления света выполняются достаточно точно только, если размеры препятствий много больше длины световой волны.

Дифракция света сопровождается интерференций. Интерферируют волны, обогнувшие препятствие.

Принцип Гюйгенса: каждая точка среды, до которой доходит волна, служит источником вторичных волн, а огибающая этих волн представляет собой волновую поверхность в следующий момент времени.

Принцип Гюйгенса-Френеля: волновая поверхность в любой момент времени представляет собой не просто огибающую вторичных волн, а результат их интерференции.

Зоны Френеля

Для вычисления результатов интерференции вторичных волн Френель придумал простой и наглядный метод – метод построения зон Френеля.

Окружим источник А сферической поверхностью σ радиусом а, много большим длины волны (a>>λ). Расстояние от точки В до ближайшей точки М₀ на поверхности сферы обозначим через b (b>>λ).

Разобьём поверхность σ на кольцевые зоны так, чтобы расстояние от краёв соседних зон до точки В отличались на половину длины волны. Преимущества подобного разбиения зон в том, что для соответствующих точек соседних зон разность хода равна λ/2 и вторичные волны от них, встречающиеся в точке В, ослабляют друг друга (так как находятся в противофазе).

Все чётные (нечётные) зоны усиливают друг друга.:

Если открыто чётное число зон Френеля, то на экране – минимум интенсивности, если нечётное – максимум.

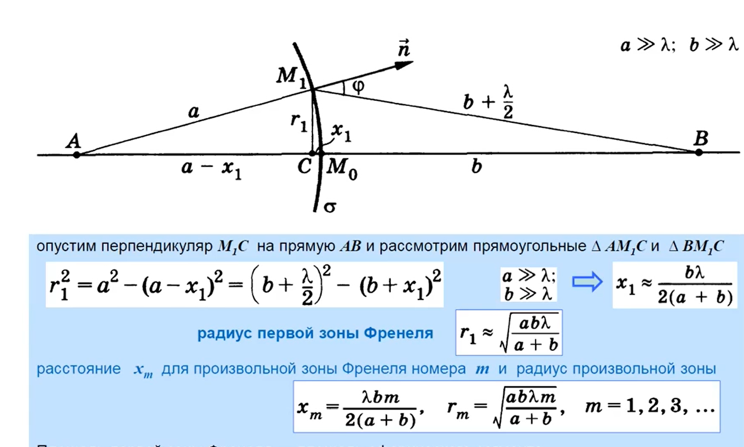
Площади зон равны, так как не зависят от m.

Полученный результат означает, что, колебания, вызываемые в точке Р(В) полностью открытой сферической волновой поверхностью, имеют такую же амплитуду, как если бы действовала только полови­на центральной зоны Френеля. Следовательно, свет от источника S в точку Р распространяется в пределах очень узкого прямого канала, т.е. прямолинейно.