
Отчет_Лаба4_ФП_Алексеева
.docУфимский государственный авиационный технический университет
ОТЧЕТ по лабораторной работе №4
по дисциплине:
«Функциональное программирование»
на тему:
«Текстовые файлы.
Факторизация, простые числа, разные задачи.»
Выполнил: бакалавр гр. ПРО-223
Алексеева А.В.
Проверил: Фридлянд Александр Михайлович
Содержание
Содержание 2
1 задание 3
2 задание 5
3 задание 7
52 задача 7
56 задача 8
Выводы 9
1 Цель работы (Вариант 3)
Выполнить задания в соответствии с вариантом №3, изучив факторизацию, работу с текстовыми файлами, простыми числами с помощью интерпретатора Hugs языка программирования Haskell; реализовав различные программы с сайта http://projecteuler.net/problems.
1. Строки исходного файла, выровненные справа.
2. (21) Let d(n) be defined as the sum of proper divisors of n (numbers less than n which divide evenly into n).
If d(a) = b and d(b) = a, where a ≠ b, then a and b are an amicable pair and each of a and b are called amicable numbers.
For example, the proper divisors of 220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110; therefore d(220) = 284. The proper divisors of 284 are 1, 2, 4, 71 and 142; so d(284) = 220.
Evaluate the sum of all the amicable numbers under 10000.
3. (200) We shall define a sqube to be a number of the form, p2q3, where p and q are distinct primes.
For example, 200 = 5223 or 120072949 = 232613.
The first five squbes are 72, 108, 200, 392, and 500.
Interestingly, 200 is also the first number for which you cannot change any single digit to make a prime; we shall call such numbers, prime-proof. The next prime-proof sqube which contains the contiguous sub-string "200" is 1992008.
Find the 200th prime-proof sqube containing the contiguous sub-string "200".
2 Результат выполнения работы
1 задание
Написать функцию, которая читает входной текстовой файл и выводит в выходной файл строки исходного файла, выровненные справа.
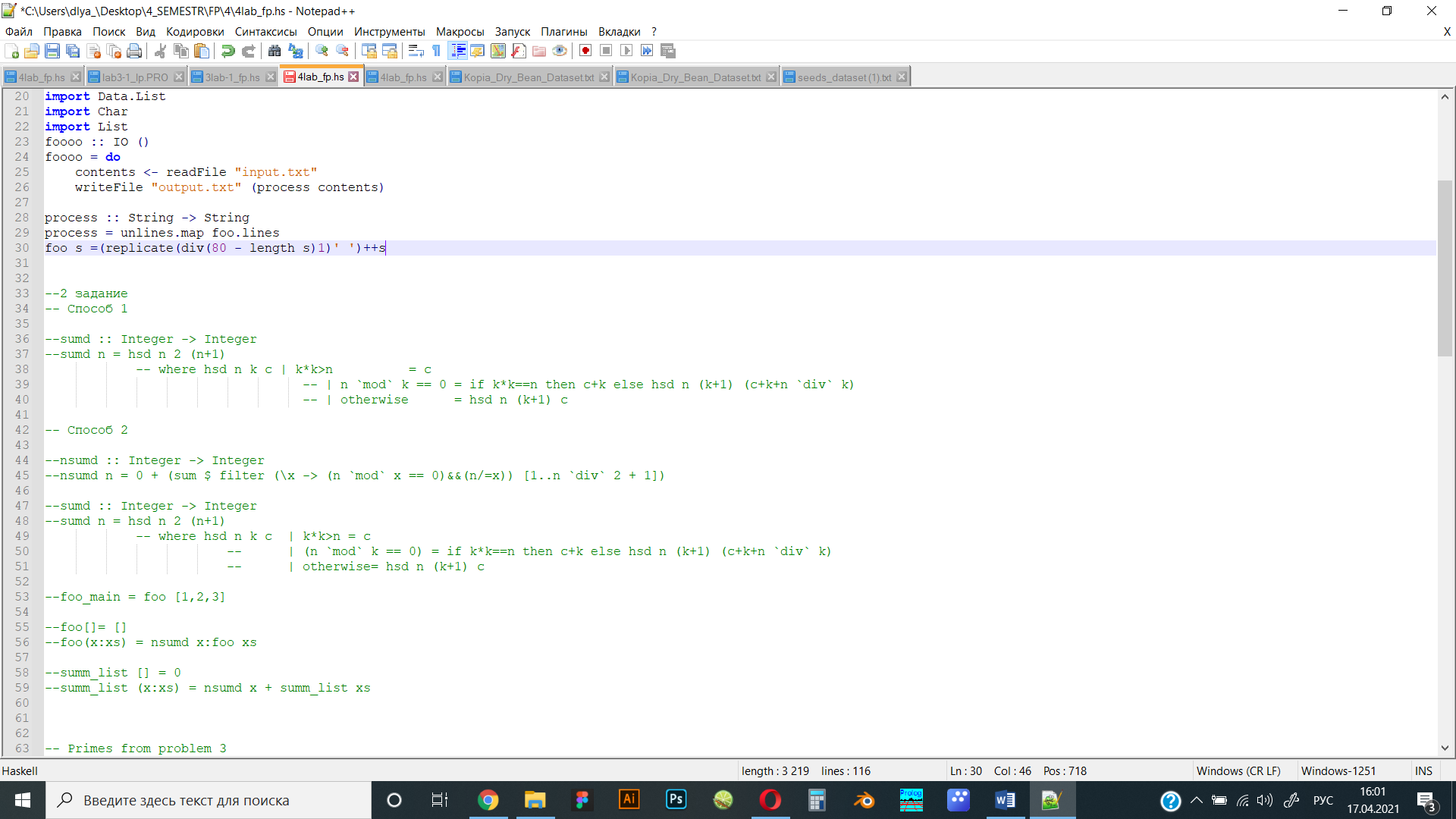
Рисунок 1 Исходный код программы в текстовом редакторе

Рисунок 2 Содержание входного текстового файла «Input.txt» задания №1

Рисунок 3 Содержание выходного текстового файла «Output.txt» с результатом выполнения задания №1
2 задание
(21) Let d(n) be defined as the sum of proper divisors of n (numbers less than n which divide evenly into n).
If d(a) = b and d(b) = a, where a ≠ b, then a and b are an amicable pair and each of a and b are called amicable numbers.
For example, the proper divisors of 220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110; therefore d(220) = 284. The proper divisors of 284 are 1, 2, 4, 71 and 142; so d(284) = 220.
Evaluate the sum of all the amicable numbers under 10000.
Перевод:
Пусть d (n) определяется как сумма собственных делителей n (чисел меньше n, которые делятся на n без остатка).
Если d (a) = b и d (b) = a, где a ≠ b, то a и b - дружная пара, и каждое из a и b называется дружескими числами.
Например, правильные делители 220: 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 и 110; следовательно, d (220) = 284. Собственные делители числа 284 - 1, 2, 4, 71 и 142; так что d (284) = 220.
Оцените сумму всех полюбившихся чисел меньше 10000.
Решение:

Рисунок 4 Исходный код
Рисунок 5 Результат
Проверка ответа:

3 задание
52 задача
(52) It can be seen that the number, 125874, and its double, 251748, contain exactly the same digits, but in a different order.
Find the smallest positive integer, x, such that 2x, 3x, 4x, 5x, and 6x, contain the same digits.
Перевод:
Видно, что число 125874 и его двойное число 251748 содержат точно такие же цифры, но в другом порядке.
Найдите наименьшее положительное целое число x , такое, чтобы 2 x , 3 x , 4 x , 5 x и 6 x содержали одинаковые цифры.
Решение:

Рисунок 6 Исходный код
Рисунок 7 Результат
Проверка ответа:

56 задача
(56)A googol (10100) is a massive number: one followed by one-hundred zeros; 100100 is almost unimaginably large: one followed by two-hundred zeros. Despite their size, the sum of the digits in each number is only 1.
Considering natural numbers of the form, ab, where a, b < 100, what is the maximum digital sum?
Перевод:
Гугол (10^100) - это огромное число: единица с сотней нулей; 100^100 почти невообразимо велико: единица, за которой следуют двести нулей. Несмотря на их размер, сумма цифр в каждом номере составляет всего 1.
Рассматривая натуральные числа вида a^b, где a, b <100, какова максимальная цифровая сумма?
Решение:

Рисунок 8 Исходный код
Рисунок 9 Результат
Проверка:

Выводы
Выполнила задания лабораторной, соответствующие моему варианту.
Уфа – 2020
