Вариант 6.
1. Все встречающиеся гласные буквы и количество их вхождений в исходный файл, отсортированный по убыванию вхождений.
2. (4) A palindromic number reads the same both ways. The largest palindrome made from the product of two 2-digit numbers is 9009 = 91 × 99.
Find the largest palindrome made from the product of two 3-digit numbers.
3. (63) The 5-digit number, 16807=75, is also a fifth power. Similarly, the 9-digit number, 134217728=89, is a ninth power.
How many n-digit positive integers exist which are also an nth power?
Вариант 7.
1. Выводит отсортированные по возрастанию цепочки символов, которые в исходном файле могут пониматься как целое число.
2. (7) By listing the first six prime numbers: 2, 3, 5, 7, 11, and 13, we can see that the 6th prime is 13.
What is the 10 001st prime number?
3. (145) Some positive integers n have the property that the sum [ n + reverse(n) ] consists entirely of odd (decimal) digits. For instance, 36 + 63 = 99 and 409 + 904 = 1313. We will call such numbers reversible; so 36, 63, 409, and 904 are reversible. Leading zeroes are not allowed in either n or reverse(n).
There are 120 reversible numbers below one-thousand.
How many reversible numbers are there below one-billion (109)?
Вариант 8.
1. Выводит отсортированные по количеству слов в предложении строки исходного файла.
2. (25) The Fibonacci sequence is defined by the recurrence relation:
Fn = Fn−1 + Fn−2, where F1 = 1 and F2 = 1.
F1 = 1 F2 = 1 F3 = 2 F4 = 3 F5 = 5 F6 = 8 F7 = 13 F8 = 21 F9 = 34 F10 = 55 F11 = 89 F12 = 144
The 12th term, F12, is the first term to contain three digits.
What is the index of the first term in the Fibonacci sequence to contain 1000 digits?
3. (160) For any N, let f(N) be the last five digits before the trailing zeroes in N!.
For example,
9! = 362880 so f(9)=36288
10! = 3628800 so f(10)=36288
20! = 2432902008176640000 so f(20)=17664
Find f(1,000,000,000,000)
Вариант 9.
1. Выводит знаки препинания и количество их вхождений в исходный файл, отсортированные по убыванию вхождений.
2. (35) The number, 197, is called a circular prime because all rotations of the digits: 197, 971, and 719, are themselves prime.
There are thirteen such primes below 100: 2, 3, 5, 7, 11, 13, 17, 31, 37, 71, 73, 79, and 97.
How many circular primes are there below one million?
3.(87) The smallest number expressible as the sum of a prime square, prime cube, and prime fourth power is 28. In fact, there are exactly four numbers below fifty that can be expressed in such a way:
28 = 22 + 23 + 24
33 = 32 + 23 + 24
49 = 52 + 23 + 24
47 = 22 + 33 + 24
How many numbers below fifty million can be expressed as the sum of a prime square, prime cube, and prime fourth power?
Вариант 10.
1. Строки исходного файла, выровненные по центру.
2. (29) Consider all integer combinations of ab for 2 ≤ a ≤ 5 and 2 ≤ b ≤ 5:
22=4, 23=8, 24=16, 25=32 32=9, 33=27, 34=81, 35=243 42=16, 43=64, 44=256, 45=1024 52=25, 53=125, 54=625, 55=3125
If they are then placed in numerical order, with any repeats removed, we get the following sequence of 15 distinct terms:
4, 8, 9, 16, 25, 27, 32, 64, 81, 125, 243, 256, 625, 1024, 3125
How many distinct terms are in the sequence generated by ab for 2 ≤ a ≤ 100 and 2 ≤ b ≤ 100?
3. (120) Let r be the remainder when (a−1)n + (a+1)n is divided by a2.
For example, if a = 7 and n = 3, then r = 42: 63 + 83 = 728 ≡ 42 mod 49. And as n varies, so too will r, but for a = 7 it turns out that rmax= 42.
For 3 ≤ a ≤ 1000, find ∑ rmax.
Пример выполнения работы
1. Написать функцию, которая читает входной текстовой файл и выводит в выходной файл указанную информацию.
Строки исходного файла, выровненные по центру.
Решение.
В данной функции предполагается, что длина строки равна 80.
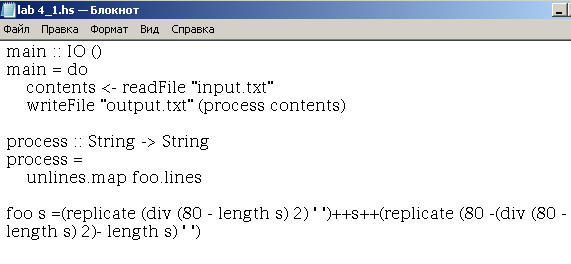
Исходный файл:
Выходной файл:
2. Перевести текст задачи и написать решение.
Bouncy numbers
Problem 112.
Working from left-to-right if no digit is exceeded by the digit to its left it is called an increasing number; for example, 134468.
Similarly if no digit is exceeded by the digit to its right it is called a decreasing number; for example, 66420.
We shall call a positive integer that is neither increasing nor decreasing a "bouncy" number; for example, 155349.
Clearly there cannot be any bouncy numbers below one-hundred, but just over half of the numbers below one-thousand (525) are bouncy. In fact, the least number for which the proportion of bouncy numbers first reaches 50% is 538.
Surprisingly, bouncy numbers become more and more common and by the time we reach 21780 the proportion of bouncy numbers is equal to 90%.
Find the least number for which the proportion of bouncy numbers is exactly 99%.
Перевод:
Задача 112.
Если при просмотре слева направо не имеется цифр, превосходящих цифры, расположенные левее, то число называется возрастающим, например, 134468.
Аналогично, если нет цифр, превосходящих цифры правее, то число называется убывающим, например, 66420.
Назовем целое положительное число, не являющееся ни возрастающим, ни убывающим, «прыгучим» числом, например, 155349.
Ясно, что не существует прыгучих чисел, меньших сотни, но уже более половины чисел, меньших тысячи (525) являются прыгучими. Действительно, наименьшее число, для которого доля прыгучих чисел впервые достигает 50%, есть число 538.
Удивительно, но прыгучие числа становятся все более и более распространенными и к моменту достижения 21780 доля прыгучих чисел равна 90%.
Найдите наименьшее число, для которого доля прыгучих чисел равна в точности 99%.
Решение.
Основной проблемой при решении подобных задач является не просто написание программы, решающей задачу, а написание эффективной по времени и памяти программы. Опишем подробно процесс нахождения решения. Сначала представляется необходимым написать проверку возрастающих и убывающих чисел, и, соответственно, прыгучих чисел:
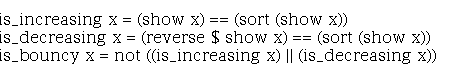
Проверка заключается в совпадении числа, преобразованного в строку, с отсортированной строкой – для возрастающих чисел, или с перевернутой отсортированной строкой – для убывающих. Проверка прыгучести, согласно определению, состоит в невыполнении первой или второй проверок.
Далее можно попробовать написать функцию, которая разбивает все числа, не превышающие заданного аргумента, на кортеж двух списков – прыгучих и всех остальных чисел, такая функция у нас определена в модуле List:
.
Тогда основная функция должна брать числа подряд, начиная с некоторого числа (логично выбрать начальное число равным 100), проверять длины полученных списков и останавливаться, когда доля прыгучих чисел достигнет заданного значения в 99%:
К сожалению, можно убедиться, что хотя эта программа работает правильно и даже вычисляет верно промежуточные числа для 50% и 90%, результата для 99% представляется невозможным дождаться в разумное время.
Конечно, проблема здесь в том, что программа крайне неэффективна по времени, ведь для каждого числа списки прыгучих и непрыгучих чисел каждый раз считаются заново с сотни.
Более эффективный алгоритм должен запоминать число прыгучих и непрыгучих чисел, меньших текущего проверяемого числа и переходить к следующему числу, пока не достигнута требуемая доля. Вот соответствующая программа:
Основная функция main имеет один аргумент p, соответствующий значению во сколько раз число прыгучих должно быть больше числа непрыгучих чисел, то есть, при р=1 доля прыгучих составляет 50%, при р=9 - 90%, при р=99 – 99%. Функция main вызывает функцию foo с начальными значениями текущего проверяемого числа – 100 и кортежем, в котором хранятся количества непрыгучих и прыгучих чисел, меньших проверяемого числа. Функция foo сначала проверяет, достигнута ли требуемая доля и в случае положительного ответа выдает текущее число, точнее, уменьшенное на единицу. Если же доля пока не достигнута, то проверяем, является ли число прыгучим и вызываем рекурсивно (причем рекурсия хвостовая) функцию с увеличенным на единицу текущим числом и увеличенным на единицу значением одного из аккумуляторов в кортеже. Вот пример выполнения функции с промежуточными результатами для проверки и требуемым ответом:
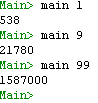
Зарегистрируемся на сайте и найдем нашу задачу по адресу https://projecteuler.net/problem=112. Введем ответ 1587000:
