

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6.4.3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
2x 2 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
dx |
|
|
|
|
x |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
t |
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
2 |
2x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 1 2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
0 x x |
|
|
|
|
|
x |
|
0; 1 t |
|
;1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
t |
|
|
t2 t |
2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
dt |
|
|
|
|
|
1 |
|
|
|
|
d t |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
2 |
|
1 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
t |
|
|
|
t |
|
|
|
|
|
|
|
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
2t |
2 |
2t |
1 |
|
2 |
|
|
|
|
|
|
1 |
2 |
|
|
|
1 |
|
2 |
2 |
|
|
4 |
|||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
lim ln |
t |
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
За ча и .
.
6.4.4.
.
e
ln x dx
0
|
|
x 0 |
|
u ln x; |
dv dx |
||
|
dx |
|
|
du |
; v x |
||
x |
|||
|
|
||
e
ln x dx.
0
,
.
.
e
x ln x e 0 dx e e 0.
0
1)
2)
1) x ln x |
|
e |
eln e lim x ln x e lim |
ln x |
|
e lim |
ln x |
|
|
|
|
|
|||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
0 |
|
x 0 |
x 0 x 1 |
x 0 |
x 1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
(0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
e lim |
x |
e lim x e. |
2) |
|
dx x |
|
e e . |
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||||||||
1 |
|
|
|
|
|
||||||||||||
x 0 |
x 0 |
|
|
|
|
0 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
x2 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
tg x |
|
|
6.4.5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
8x |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
41
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
4 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
). |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
0 tg x 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
tg x |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
8x |
8x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
8x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4 |
|
dx |
|
|
|
|
|
1 |
|
4 |
|
dx |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
8x |
|
|
|
|
|
x |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
8 |
4 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
tg x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
exdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
6.4.6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 4 4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ex |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3;4 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 4 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 4 |
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
). |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ex 1 |
|
|
|
|
|
|
|
|
|
|
|
|
ex |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
. |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 4 4 |
x 4 4 |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
4 4 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4 |
|
|
dx |
|
|
|
x 4 3 |
|
4 0 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
4 0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
||||||||||||||||
|
3 x 4 4 |
|
|
|
|
3 |
|
|
|
|
|
|
3 x 4 3 |
|
|
|
|
|
|
|
x |
4 3 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 x 4 0 |
|
|
3 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
exdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 x 4 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6.4.7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
42

dx
sin5 x
2
x y, |
dx dy |
||||
x |
|
y |
|
||
|
2 |
||||
|
2 |
|
|
||
x y 0 |
|||||
|
|
|
|
|
|
|
|
|
0; |
|
|
|
|
|
2 |
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
dy |
dy |
|
|
|
2 |
|
|
dy |
|
||
|
|
|
|
|
|
|
|
|
. |
|||
|
y |
|
|
|
|
|
|
|||||
sin5 |
sin5 |
y |
0 sin5 y |
|||||||||
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
f y |
1 |
|
|
0 . |
|||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
sin5 |
|
|
||||||
|
|
|
|
|
|
y |
||||||
|
f y |
|
1 |
|
lim |
lim |
sin5 y |
||
y |
|
5 |
||
y 0 |
y 0 |
1 |
||
|
|
|
y |
|
6.2.4.
|
|
y |
|
5 |
|
|
|
|
lim |
|
|
|
1. |
|
|
||
|
|
|
|
|||||
y 0 |
sin y |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
dy |
|
|
|
|
, |
|
|
|
||
|
|
|
|
|
||||
|
|
|
sin5 |
y |
||||
|
|
|
|
|
0 |
|
|
|
|
y |
1 |
, |
||
|
y5 |
||||
|
|
|
|||
|
|
|
|
||
2 |
dy |
|
|||
|
|
|
|
||
y5 |
|
||||
0 |
|
|
|
|
|
6.3.2.
6.5.
|
2 |
|
|
dx |
|
2 |
|
xdx |
|
||
6.5.1. |
|
|
|
. |
6.5.2. |
|
. |
||||
|
2 |
4x 3 |
|
|
|||||||
|
0 |
x |
|
|
1 |
|
x 1 |
||||
0 |
|
e1/ x dx |
|
|
|
|
|
||||
6.5.5. |
|
|
|
. |
|
|
|
|
|
||
|
|
x3 |
|
|
|
|
|
||||
1 |
|
|
|
|
|
|
|
|
|
||
1
6.5.3. x ln xdx .
0
|
: |
|
|
1/e |
|
dx |
|
6.5.4. |
|
||
|
|
. |
|
|
x ln2 x |
||
0 |
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
x2dx |
|
|
|
1 |
|
dx |
|
|
||||
|
|
xdx |
|
|
|
|
|
|
|
|
|
||||||||||||
6.5.6. |
|
|
|
|
|
|
|
. 6.5.7. |
|
|
|
|
|
|
|
. 6.5.8. |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||
|
1 x |
4 |
|
3 |
(1 x |
2 |
) |
5 |
e |
x |
|
||||||||||||
0 |
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|||||||||||
. |
6.5.1. |
|
|
. 6.5.2. 8 / 3 . |
6.5.3. |
|
1/ 4 . 6.5.4. 1. 6.5.5. |
2 / e . |
|||||||||||||||
6.5.6. |
|
|
|
|
|
|
. 6.5.7. |
|
|
|
|
|
|
. 6.5.8. |
|
|
|
|
|
. |
|
||
43
7. .
7.1.
?
7.2. a
7.3.
t tg x ?
7.4.
7.5.
y (x 1) f (x) ,
7.6.
7.7.
7.8.
,
7.9.
7.10.
.
7.1. 21. 7.2. 6 . 7.3.
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
y x2 , |
||
i |
[0; 4] |
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||
|
( i 1, 2, 3, 4) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
(x 2)2 dx 21? |
|
|
|
|
|
|||||||||
|
|
|
|
3 |
|
|
3 /4 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
sin2 x 4cos2 |
x |
|
|
|
|||||||
|
|
|
|
|
|
|
/4 |
|
|
|
|
|
|
|
|
|
||
2 |
|
ex |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx ? |
|
|
|
|
|
|
|
|
|
|
|
|
||||
ex 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
||
|
|
x 0 , |
x 2 |
|
|
|
|
, |
|
f (x) – |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
[0; 2] ? |
|
|
|
|
|
||
|
|
|
|
y |
2 |
|
|
|
1 |
|
|
, 1 x 4 ? |
|
|
|
|||
|
|
|
|
|
x3 |
|
|
|
||||||||||
|
|
|
|
|
|
x |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
3 2cos ? |
|||||||
|
, |
|
|
|
|
|
|
|
|
– |
0 y |
|
, |
|||||
|
|
|
|
|
|
|
|
|
1 x2 |
|||||||||
–?
dx
2 x2 4x 8 ?
1
dx
0 tg x x ?
|
1 |
2 |
. 7.4. ln e 1 . |
7.5. (1 x) f (x)dx (x 1) f (x)dx . |
|
|
0 |
1 |
7.6. |
31 |
. |
7.7. 11 . 7.8. |
4 |
. |
7.9. . 7.10. |
. |
|
|
||||||
6 |
|
3 |
|
4 |
|
||
44
|
|
8 |
|
|
|
|
8. |
|
|
|
|
|
|
8.1. |
|
|
|
|
|
|
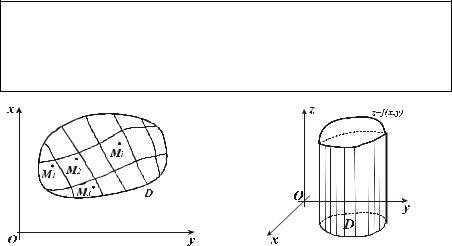
D |
|
xOy |
|
|
|
Di , |
z f (x, y) . |
|
D |
|
|
|
|
|
|
|
Mi (xi , yi ) |
( . |
. |
8.1). |
( |
) |
|
|
max diamDi . |
||
diamDi |
|
|
|
i |
|
|
|
|
|
Di . |
|
|
|
f (Mi ) Si . |
|
|
|
|||
f (Mi ) f (xi , yi ) , |
|
Si – |
||||
|
i |
|
|
|
|
|
|
Di . |
|
|
|
|
|
. |
|
f (x, y)dxdy |
|
|
|
|
|
lim , |
D |
|
|
|
|
|
|
|
|
|
|
|
D , |
0 |
Mi . |
z f (x, y) |
|
|
|
|
|
|
||||
( |
|
) |
D . |
|
|
|
. 8.1 |
|
|
|
. 8.2 |
|
|
z f (x, y) , |
– |
|
|
D . |
|
|
f (x, y)dxdy |
|
|
|
|
, |
|
D |
f (x, y) 0. |
|
|
|
|
|
8.2, |
|
|
|
|
||
z f (x, y) , |
|
|
D , |
|
|
|
z 0 , |
, |
|
Oz . |
|
, |
|
|
|
|
|
|||
|
|
45 |
|
|
|
|
z f (x, y) |
|
|
|
D . |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|||||||
8.1.1. |
( f1(x, y) kf2 (x, y))dxdy f1(x, y)dxdy k f2 (x, y)dxdy |
( |
|
|||||||
|
D |
|
|
D |
|
D |
|
|
|
|
|
). |
|
|
|
|
|
|
|
|
|
8.1.2. |
1 dxdy SD ( |
|
|
D ). |
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
8.1.3. |
f (x, y)dxdy f (x, y)dxdy f (x, y)dxdy , |
|
D D1 D2 |
|
||||||
|
D |
D1 |
|
|
D2 |
|
|
|
|
|
D1 D2 , |
|
D1 |
D2 |
|
|
|
|
( |
|
|
|
|
). |
|
|
|
|
|
|
|
|
8.1.4. f (x, y)g(x, y)dxdy |
f (x*, y* ) g(x, y)dxdy , |
f (x, y) |
|
|
||||||
|
D |
|
|
|
D |
|
|
|
|
|
|
D , |
g(x, y) |
|
|
|
|
. |
|
f (x*, y* ) – |
|
|
|
f (x, y) |
|
|
|
|
|
D |
( |
|
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8.2.1. |
|
. ( |
|
|
|
|
|
|
.) |
|
|
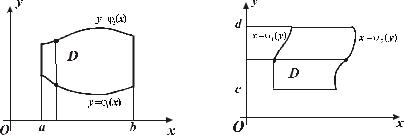
[a,b] |
|
|
|
y 1(x) |
y 2 (x) , |
|
|||
1(x) 2 (x) , |
|
|
z f (x, y) |
|
|
|
|
D , |
||
|
|
x a , |
x b , |
y 1(x) , |
y 2 (x) ( |
. |
8.3). |
, |
||
|
|
|
|
|
|
|
|
2 ( x) |
|
|
|
|
x [a,b] |
|
|
|
F (x) |
f (x, y)dy |
|
||
|
|
|
|
|
|
|
|
1 ( x) |
|
|
|
F (x) |
|
|
[a,b] , |
|
|
|
|
||
f (x, y)dxdy |
|
|
|
b |
b |
2 ( x) |
|
|
|
|
|
|
|
F (x)dx dx |
f (x, y)dy . |
|
|||||
D |
|
|
|
|
a |
a |
1 ( x) |
|
|
|
. 8.3 |
. 8.4 |
46

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y , |
|
|
|
|
|
|
|
|
x . |
|
|
|
|||
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
D . |
|
|
|
|
|
, |
|
|
|
|
|
|||||
. 8.4. |
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
d |
2 ( x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
: |
|
|
f (x, y)dxdy dy |
|
|
|
f (x, y)dx |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
D |
|
|
|
|
c |
1 ( x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
, |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
, |
|
||
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
- |
|
, |
|
|
|
|
|
8.1.3, |
|
|
|
|
z f (x, y) |
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|||||
|
|
|
|
|
|
|
f (x, y)dxdy |
|
|
|
|
|
|
|
|
|
|
|
g(x, y) 1). |
|
||||||||||
|
|
f (x, y) |
|
|
D |
|
|
|
|
( . |
|
|
|
|
8.1.4 |
|
|
|
|
|||||||||||
|
|
|
|
dxdy |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8.3. |
|
|
|
|
|
|
D |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
8.3.1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
xexy dxdy |
|
|
|
|
|
|
|
|
|
|
|
D : |
||||
1 x 2 , 0 y 2. |
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x , |
y |
|
|
|
|
|
|
|
|
|
|
— |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
, |
|
|
|
|
|
|
. |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y , |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
2 |
|
e |
xy |
|
2 |
2 |
|
e |
2 x |
|
|
2 |
|
e |
4 |
|
e |
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
xexy dxdy xdx exy dy xdx |
|
|
|
|
(e2 x 1)dx |
|
x |
|
|
|
|
2 |
|
1 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
D |
1 |
0 |
|
1 |
|
x |
|
0 |
1 |
|
|
2 |
|
|
1 |
2 |
2 |
|
|
|||||||||||
|
e4 e2 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
e xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
8.3.2. |
, |
|
|
|
dxdy |
4 , |
D — |
|
|
0 x 1, 0 y 1. |
|
|||||||||||||||||||
|
1 x2 |
|
|
|
||||||||||||||||||||||||||
. |
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8.1.4, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
47 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
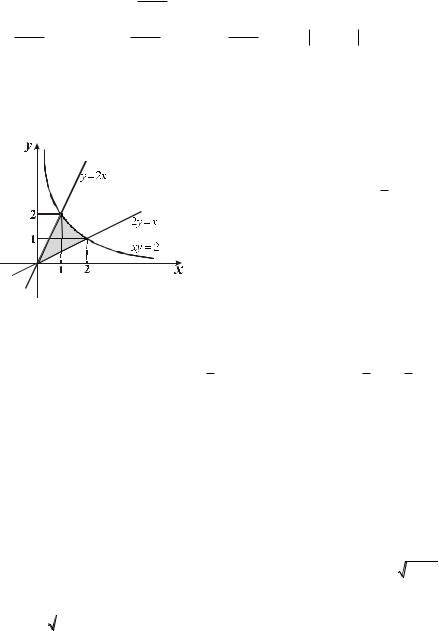
f (x, y) e xy |
g(x, y) |
1 |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
e xy |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
dxdy |
|
|
|
1 |
1 |
dx |
|
|
|
|
|
|
|
|
|
||||
|
* |
* |
|
|
* |
* |
dy |
|
* |
* |
1 |
|
1 |
|
* |
* |
|
||||||
1 x2 dxdy e x y |
|
1 x2 |
e x y |
1 x2 |
e x y |
|
y 0 |
arctg x 0 |
|
4 e x y |
|
|
4 |
||||||||||
D |
|
|
|
D |
|
|
|
|
|
0 |
0 |
|
e xy |
|
|
|
|
|
|
|
|
|
|
|
xy 0 . |
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8.3.3. |
|
|
|
|
|
|
|
|
|
|
|
|
f (x, y)dxdy |
|
|
|
|
|
|
D , |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 2x 0 , 2 y x 0 , xy 2 . |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x y 2x , |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
x 0 |
2 |
y 0 , |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
, |
y 2x |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
x 2 y |
|
|
|
|
|
|
xy 2 . |
||||
|
|
. 8.5 |
|
|
|
|
|
|
|
|
, |
|
|
x 0 |
|
|
y 0 , |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
(1, |
2) |
(2, 1) . |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
. 8.5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||
|
|
|
|
|
|
|
x y 2x |
|
|
|
x y 2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
x [0, 1] |
|
|
||||||||||
x [1, |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
x |
|
|
||
2] , |
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y ) |
|
|
|
|
||
|
x 1 |
|
|
|
|
|
, |
|
|
|
|
x [0, 2], |
|
|
D |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8.1.3: |
|
|
|
|
|
|
|
|
|
1 |
|
2 x |
|
|
|
2 |
|
2/ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x, y)dxdy dx |
f (x, y)dy dx |
f (x, y)dy . |
|
|
|
|
|
|
|
|
|
|
|||||||||||
D |
|
0 |
|
x/2 |
|
|
|
1 |
|
x/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8.3.4. |
|
|
f (x, y)dxdy |
|
|
|
|
|
|
|
D |
|
|
|
|
|
, |
|
|
y | x | , |
y |
|
|
|
|
D |
2 x2 |
||||
( . 8.6). |
|
|
|
|
1 x 1, |
||
. |
, |
D |
|
||||
| x | y |
|
( |
|
|
|
|
|
2 x2 |
|
|
|
|
|
||
48
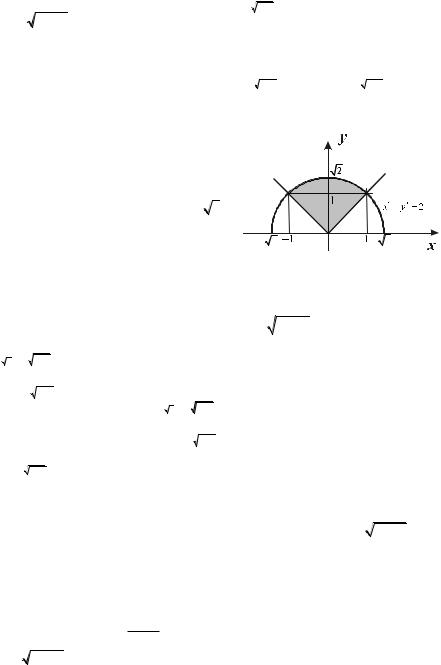
|
|
|
|
|
|
|
|
|
1 |
2 x2 |
|
|
|
|
| x | |
2 x2 ), |
|
: |
f (x, y)dxdy dx |
|
f (x, y)dy . |
|
, |
||||||
|
|
|
|
|
|
D |
|
|
1 |
|x| |
|
|
|
|
| x | x |
|
|
x [ 1, 0] |
| x | x |
|
x [0, 1]. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
0 |
2 x2 |
|
1 |
2 x2 |
|
|
|
|
|
|
|
|
|
: dx |
|
f (x, y)dy dx |
|
f (x, y)dy , |
||
|
|
|
|
|
|
|
|
|
1 |
x |
|
0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
D . |
|
|
|
|
|
|
|
|
y 1, |
|
|
Y X |
|
|
Y X |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
y [0, 2] . |
|
|
|
|
|
|
||
y x y , |
|
y [0,1] |
|
|
|
2 |
|
|
|
2 |
||||
1 |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
dy f (x, y)dx . |
|
|
|
|
|
|
|
. 8.6 |
|
|
||||
0 |
y |
|
|
|
|
x |
y |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
: |
x |
2 y2 . |
|
|
|
|
|
2 y2 |
|
|
|
|
|
|
|
|
|
|
|
: |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
dy |
f (x, y)dx . |
|
|
, |
|
|
|
|
|
|
|
|||
1 |
2 y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
y |
|
2 |
2 y2 |
|
|
|
|
|
|
|
|
|
D : dy f (x, y)dx dy |
f (x, y)dx . |
|
|
|
|
|||||||
|
|
|
0 |
y |
|
1 |
|
2 y2 |
|
|
|
|
|
|
8.3.5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
3x 9 |
|
|
2 |
4 2x |
|
|
|
|
|
|
|
|
|
dx |
|
f (x, y)dy dx |
|
f (x, y)dy . |
|
|
|
|
|
|
||||
3 |
0 |
. |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 y |
3x 9 |
||
|
|
|
0 y 4 2x |
|
|
. |
|
|
|
|||||
x [ 3,0] |
|
x [0,2]. |
|
|
, |
x 0 |
|
|||||||
|
, |
|
|
|
|
|
|
|
, |
y 3. |
|
8.7 |
||
|
|
|
|
, |
|
|
y [0,3]. |
|
|
|
|
|
||
|
|
|
x |
|
9 |
|
|
|
|
|
|
|||
|
|
|
|
x y2 |
( |
|
x |
|
|
|
|
|
||
y |
3x 9 ), |
|
3 |
|
|
|
|
|
|
|
|
|||
— |
x log2 (4 y) ( |
|
x |
|
|
|
||||||||
|
|
|
|
|
|
|
|
49 |
|
|
|
|
|
|
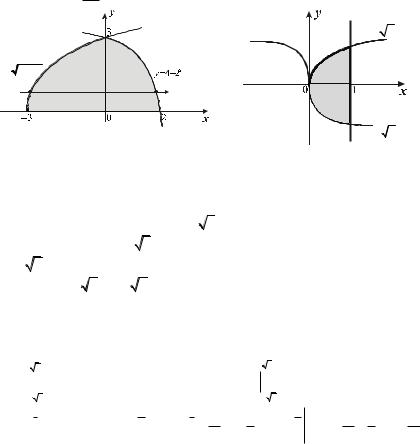
|
|
|
y 4 2x ). |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
(4 y ) |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
3 |
log2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
: dy |
|
|
f (x, y)dx . |
|
|
|
|
|
|
|
|
|
|||
|
|
|
0 |
|
y2 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
X |
|
Y |
3X 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y 3 |
X |
|
|
|
|
|
|
|
. 8.7 |
|
|
|
|
|
|
. 8.8 |
|
|
|
|
8.3.6. |
|
|
|
|
|
|
|
|
(21xy2 52x2 y3 )dxdy , |
|
|
D |
|||||
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
y3 x 0 , |
y x , x 1. |
|
|
|
|
|
||||
|
|
. |
|
|
|
|
y x |
|
|
|
|
x 0 . |
y3 x 0 |
|
|
||
y 3 |
x . |
|
|
|
, |
|
|
|
|
x [0, 1] |
y |
|
|
|
|||
|
|
|
|
3 |
x y |
x ( . |
|
. |
8.8), |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
. |
0 |
1: |
(21xy2 |
52x2 y3 )dxdy |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x |
|
|
|
|
|
1 |
|
|
13x2 y4 |
x |
|
|
|
|
|
dx |
(21xy2 |
52x2 y3 )dy dx 7xy3 |
|
|
|
|
|
||||||||||
0 |
3 x |
|
|
|
|
|
0 |
|
|
|
|
3 x |
|
|
|
|
|
1 |
|
5 |
|
|
|
|
|
10 |
|
7 |
|
|
13 1 |
2 13 7 3 71 . |
|||
(7x2 13x4 7x2 13x 3 )dx 2x 2 |
13 x5 7 x2 3x 3 |
||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
5 |
3 |
0 |
5 |
3 |
|
15 |
8.3.7. |
|
|
|
|
|
|
|
|
|
|
x2 cos(xy)dxdy , |
|
|
D |
|||
|
|
|
|
|
|
|
y 0 , x , |
|
|
D |
|
|
|
|
|
||
|
|
|
|
|
|
|
y x . |
|
|
|
|
|
|
||||
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
0 y x , |
x [0, ]. |
||
|
|
|
|
|
, |
— |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
( |
) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
