Райцин / Практикум 2 часть

Добавил:

Morze Developer Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский технический университет связи и информатики

Предмет:

Высшая математика

Файл:

( A, dr ) x

.pdf

Скачиваний:

113

Добавлен:

16.01.2023

Размер:

5.12 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1511 12 13 14 15 > Следующая >>>

rot A

	rot( A B) rot A rot B ,		.
:	rot( A B) rot A rot B ,		—
.
,	(	,
)			.
16.2.	.

( A, dr )	A		2-
( A, dr )			L .
L
A
,	L	–	-
,
-			,
L :
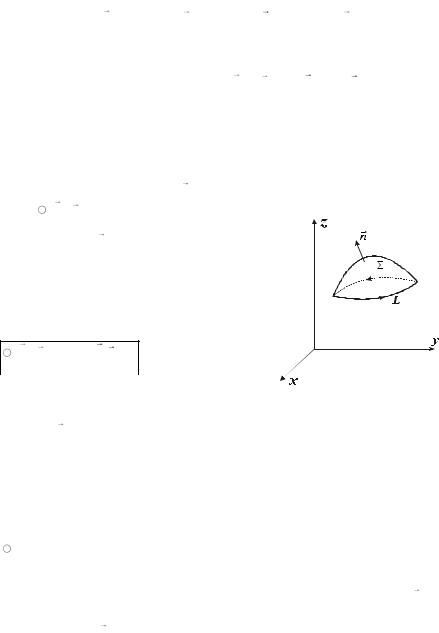
( A, dr ) (rot A, n)d (			).

. 16.1

n ,

(

. 16.1).

(

. .

14.3)

Pdx Qdy Rdz

cos

cos d

cos ,

cos –

L ,

P ,

–

A .

101

16.3.

16.3.1.

A yzi xzj (x y)k .

P yz ,

Q xz

R x y .

rot A

x y

xz 1 x ,

rot A

x y y 1,

rot A

yz z z 0 .

, rot A (x 1)i ( y 1) j .

16.3.2.

A {y2 , 2xy, 2 y}

x 1, y cost ,

z sin t ,

y2 z2 1

x 1.

L ,

n i .

rot A

2i ,

(rot A, n) 2 .

2xy

2 y

( A, dr )

16.3.3.

L : x cost, y sin t,
	z 2(1 cost)
t .
.
,	,
,
,	t
	,

(2)d 2S 2 ,	S –		,
.
A (z y)i (x z) j ( y x)k
,
		.
x2 y2 1	,	L —	,
x2 y2 1		z 2 2x .

L ,

2x z 2 0

	2		1
, . . n		, 0,		.

	5		5
	5		5

102

											:
					i				j			k
rot A														2i 2 j 2k .
rot A				x					y			z		2i 2 j 2k .
				x					y			z
		z y						x z			y x
(rot A, n)							2	2 0 2					1		2				6	.
																				.
							5						5					5
							5						5					5
( A, dr ) (rot A, n)d																6			d		6S		.
																			d				.
																5
L																5						5
z 0																		x2 y2 1,										,
		1							.																	2x z 2 0				z 0
						,																			S		( A, dr ) 6 .
																										5

		5
		5																										L
																									,
									: ( A,dr ) (z y)dx (x z)dy ( y x)dz
										L					L
2
	(2 2cost sin t)(sin t) (cost 2 2cost)cost (sin t cost) 2sin t																												dt
							z y					xt								x z				yt	y x			zt
0							z y					xt								x z				yt	y x			zt
2																								02
(2sin t 2cost 3)dt 2cost 2sin t 3t																									6 .
																									6 .

0
16.3.4.																				A y2i xyj (x2 y2 )k										L ,
																	x2 y2 z								x 0 ,			y 0 ,		z 1
x 0 ,			y 0 .										L
																									z .
		.																(				. 16.2).
		.

		,														,
		,				n							, . .
						n							, . .
								,								.							L ,
								,					.										L ,
													.
											( A, dr ) (rot A, n)d
											L
																												. 16.2

103

		i		j		k
rot A									2 yi 2xj yk .													,

		x		y		z
		x		y		z
		y2		xy	x2 y2
. 13.1,					,						xOy .								,
. 13.1,					,						xOy .													:
							Dxy				1.													:
z (x, y) x2 y2 ,														P 2 y ,			Q 2x ,		R y .					,
	,				.		13.1,									,								,
	(rot A, n)d							Oz ,		y							( y 2 y 2x 2x 2 y)dxdy
									x	y		z ( x, y)
							R P			Q				dxdy
					Dxy											Dxy
				/2	1					/2	1							/2	r	3	1	1
				/2	1					/2	1									3	1
											2
ydxdy d r sin rdr											sin d r				dr cos			0					.
																							.
																			3			3
	Dxy		0		0					0	0										0	3
	Dxy		0		0					0	0										0
	,								( A, dr )				1	.
	,								( A, dr )					.
									L		3
									L
16.3.5.															A yzi xzj (x y)k
		,		x y 0.														x2 y2 2z2 2
				x y 0.

						,
				x2 y2 2z2 2 .
1			1			1
n		;		;0	cos		,
n		;		;0	cos		,
	2		2			2
							(rot
x2 z2	1.					,
			xOz

( A, dr ) 2 d (r cos 1)rdr

		16.3.1.										,
												x y 0
													x y 0
(rot A, n) x							1	y 1			x y 2 .
(rot A, n) x							1				x y 2 .
					2	2								2
A, n) x			y	2						2(x			1)

															2(x 1) .
															2(x 1) .
		2					y x					2
		2					y x					2
							y : x2 ( x)2 2z2 2 ,
1.												:
1.												:
	(x 1)	dxdz					2					(x 1)dxdz .
	(x 1)	cos					2					(x 1)dxdz .
x2 z2 1		cos				:			x2 z2 1
2						:			2
2		1							2			1
2	cos d r 2dr 2 d rdr 2 .

L	0	0	0	0	0	0
				0	2	1/2

104

16.4.

									z		x
16.4.1.	rot A ,	:	)	A z3i y3 j x3k ;		) A	y	,	z	,	x	.
16.4.1.	rot A ,	:	)	A z3i y3 j x3k ;		) A		,		,		.
				)		z		.	x		y
16.4.2.		14.5.5		)				.
16.4.3.					A z2i x2 j y2k
x2 y2 z2 1					x y z 1
				n {1, 1, 1} .
16.4.4.					A {x,2z, y}
x cost,
												t .
y 2sin t,												t .

z 3cost - sin t 1,								.
								.
16.4.5.					A 2xi 2zj yk
ABOCDA ,	O (0, 0, 0) ,		A (1, 0, 0) , B (1, 2, 0) , C (0, 2, 3) , D (0, 0, 3) —
				,	.	,
				,	.	,
					.	A (xz y)i yzj 2xyk
16.4.6.						A (xz y)i yzj 2xyk
,	x 0 , y 0		z 5		x 0, y 0 .	x2 y2 z2 16 0
	x 0 , y 0		z 5		x 0, y 0 .

			2	x	2			x2 y2
16.4.1.	) 3(z					) j ;	)
16.4.1.	) 3(z					) j ;	)		2
								xy
16.4.4.	6 .	16.4.5. 3 .					16.4.6.		9
16.4.4.	6 .	16.4.5. 3 .					16.4.6.
									4

17.

17.1.

	y2	z2			z2 x2
	y2	z2			z2 x2
,				,			. 16.4.3.	14 3 / 9 .
,	yz		2	,	zx	2	. 16.4.3.	14 3 / 9 .
	yz				zx

					f (M )	grad f ,
			u f (x, y, z)			:
grad f	f	i	f	j	f k .	Д1Ж, 21.1.2.
	x		y		z

105

									f (x, y, z)
				.			.		(	):

			,		,			.
	x		,	y	,			.
	x			y			z		,	,
									,	,
						.		.	,
grad f		f				.

:(a b) (a) (b) .

,–

: (ab) a (ab) b (ab) .

b .

17.2.

A {P,Q, R}

				,
A :	A grad	,	P	,
				x
				x

A : div A (, A) .

: rot A [, A] .

		,	,	,
		,
a		b –	,
	.		(
			(
	"		"	a
				a
			,	,
			,

	,
(x, y, z) , . .
Q	, R	.
	y	z

	,	,	A	D ,
	rot A 0		,	:
1)	rot A 0		D ;	L D
2)			-	L D
	:	( A, dr ) 0 ;
		L
3)			,	M1 M 2
	D ,		,

:( A, dr ) (M 2 ) (M1) .

,	-
,	:
	106

(M ) Pdx Qdy Rdz C

M 0

–

(x0 ; y0 ; z0 ) ; M (x, y, z) –

D ;

C –

A {P,Q, R}

Pdx Qdy Rdz

(x, y, z) .

17.3.

A {P,Q, R}

v :

A rot v

v(x, y, z)

A .

D ,

1) div A 0

D ;

: ( A, n)d 0 ;

L ,

( . 16.1).

: v1 v2 grad f ,

v2 –

A .

0 ,

A rot v

Pi Qj Rk

P ,

x Q ,

R .

v v1

grad f ,

f –

A .

107

17.4.			,
17.4.1.	:	1)	div( f A) ( A,grad f ) f div A ;
2) rot( f A) [grad f , A] f rot A .
.	1) div( f A) ( f A) f ( f A) A ( f A) (A, f ) f (, A)

( A,grad f ) f div A .

2) rot( f A) [, f A] [ f , f A] [A, f A] [ A, f ] f [, A]

[ A,grad f ] f rot A [grad f , A] f rot A .								,
						.
17.4.2.	rot[r ,[c,r ]] ,	r {x, y, z} –					(x, y, z) ,
c –	.
.
[b,[a,c]] b(a,c) c(a,b)		:
rot[r ,[c,r ]] rot(c r2 r (c,r )) rot(c r2 ) rot(r (c,r )) .
	2)	17.4.1,		rot(c r2 ) [grad r2 ,c] ,
rot(r (c,r )) [grad(c,r ),r ] (c,r ) rot r .
grad r2 grad(x2	y2 z2 ) 2xi 2yj 2zk 2r ,
				i	j		k
				i	j		k
grad(c, r ) grad(cx x cy y cz z) cxi cy j czk c ,			rot r					0 .
grad(c, r ) grad(cx x cy y cz z) cxi cy j czk c ,			rot r	x	y		z	0 .
				x	y		z
				x	y		z

rot[r ,[c,r ]] [2r,c] [c,r ] 3[r,c] .

17.4.3., rot rot A grad div A 2 A .

	.									( .
17.4.2),								rot rot A [,[A]] (, A) (,) A div A 2 A .
								grad div A ,			A
							.		. .	(			),

2			2		2		2	.					,
	2			2		2
		x		y		z
										,		.
							.			,	rot rot A grad div A A	.

108

17.4.4.

A {2xy z, x2 2y, x}

rot A

i (x) y

(x2 2 y)z

2xy z

x2 2 y

j ((x) (2xy z) ) k ((x2 2 y) (2xy z) ) 0 i (1 1) j (2x 2x)k 0 .

. 17.2,

M 0

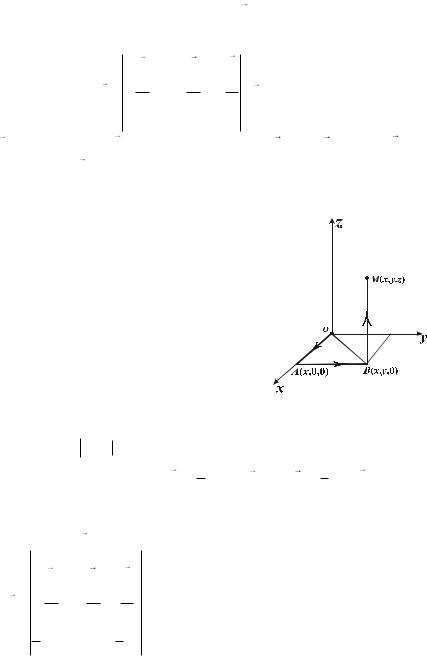
M (x, y, z) ,

OABM

(

. 17.1).

(M ) Pdx Qdy Rdz C ,

OA y z 0 ,

(dx 0) ,

z 0 ,

(dx dy 0) .

P 2xy z

. .

y z 0 .

(M ) (x2 2 y)dy xdz C .

. 17.1

(M ) x2 y y2 y xz z

C x2 y y2 xz C .

17.4.5.

ln x

ln z

1 k

M1(2, 2, 2) .

M0 (1, 0, 1)

x 0 ,

z 0 .

rot A

y ln z

ln x

x 1

109

	P	y	ln z	,
x
		x

F( y, z) –

y

y
	ln z dx y ln x		x ln z F ( y, z) ,
	ln z dx y ln x		x ln z F ( y, z) ,
x		z ,
	y	z ,
		x .
Q ln x ,	,

(x, y, z) ,

y ln x x ln z F ( y, z) ln x ,

F 0 , . .

F( y, z) G(z) .

G(z)

1, .

G(z) z C .

y ln x x ln z G(z) z

y ln x x ln z z C ,

C –

M 0 M1

M1		(2, 2,2)
( A, dr ) (M1) (M0 ) y ln x x ln z z

		(1,0,1)
		(1,0,1)
M0

2ln 2 2ln 2 2 1 1 .

17.4.6.

A {x2 , y2 , xy 2xz 2 yz}

. div A

(x2 )

( y2 )

(xy 2xz 2 yz) 2x 2 y 2x 2 y 0 ,

. 17.3,

vz 0 ,

P x2

x Q y2

vy x2 z F1(x, y) ,

vx y2 z F2 (x, y) ,

F1(x, y)

F2 (x, y) –

x R xy 2xz 2 yz ,

F1 2 yz

F2 xy 2xz 2 yz .

vx ,

2xz

F2 (x, y) 0 ,

	F									x2 y
	1	xy ,					F1(x, y)				.
		xy ,					F1(x, y)			2	.
	x						y			2
			2			2	y
	v y			z i	x			z	j grad f
	v y			z i	x			z	j grad f
							2
17.4.7.							,			A ,
				.				,		,
				.						,

A graddiv A rot rot A .

f (x, y, z) –

A 0 .

17.4.3, ,

(

110

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1511 12 13 14 15 > Следующая >>>

Соседние файлы в папке Райцин

#
16.01.202367.07 Кб94вопросы к экз.doc
#
16.01.2023766.72 Кб105Матан ответы тест.pdf
#
16.01.20231.39 Mб161Практикум 1. 2-е.pdf
#
16.01.20235.12 Mб113Практикум 2 часть.pdf
#
16.01.20231.22 Mб113СИДЗ_1 (высшая матеиатика).pdf
#
16.01.2023109.57 Кб112Таблица неопределенных интегралов.doc
#
16.01.2023123.91 Кб106таблица производных и дифференциалов.pdf