

1)нет;
2)12 x2 yz c ;
3)12 ( y2 z z2 y) x c ;
#4) 12 ( y2 z2 2x) c ;
5)12 ( y2 z2 2x) c ;
3.16.3.Является ли векторное поле F P;Q; R потенциальным? Если да,
найти его скалярный потенциал.
|
|
|
z |
|
z |
|
1 |
|
|
|
|
|
|||||
F |
|
; |
|
; |
|
|
||
x2 y |
xy2 |
|
||||||
|
|
|
|
|
xy |
|||
1)нет;
2)z 1 1 c ;x y
3) |
z |
c ; |
x2 y2 |
#4) xyz c ;
5)z2 c xy
3.16.4.Является ли векторное поле F P;Q; R потенциальным? Если да, найти его скалярный потенциал.
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
F x xz2 |
; |
|
; z zx2 |
|
|||
y |
|||||||
|
|
|
|
|
|
||
1)нет;
2)x2 xz z2 ln y c ;
3)12 (x2 xz z2 ) ln y c ;
4)12 (x2 z2 ) ln y c ;
#5) 12 (x2 z2 x2 z2 ) ln y c
3.16.5. Является ли векторное поле F P;Q; R потенциальным? Если да, найти его скалярный потенциал.
F2xy z; x2 2 y; x
1)нет;
31
2) xy2 y2 12 z2 c ; #3) x2 y y2 xz c ;
4)x2 y y2 12 x2 z c ;
5)xy2 y2 xz c
3.16.6.Является ли векторное поле F P;Q; R потенциальным? Если да,
найти его скалярный потенциал.
Fxy; yz; zx
1)12 x2 y y2 z z2 x c
2)xyz c
3)12 y2 x z2 y x2 z c
#4) не является
5)12 z2 x c
3.16.7.Является ли векторное поле F P;Q; R потенциальным? Если да,
найти его скалярный потенциал.
F y; x z; y z
#1) xy yz z2 c
2
2) не является
3) xy yz y2 c
2
4) yz xz z2 c
2
5) xy yz x2 c
2
3.16.8. Является ли векторное поле F P;Q; R потенциальным? Если да, найти его скалярный потенциал.
F yz; xz; xy #1) xyz c
2)12 x2 y y2 z z2 x c
3)12 x2 z y2 x z2 y c
4)не является
32

5)12 x2 y z 12 y2 x z 12 z2 x y c
3.16.9.Является ли векторное поле F P;Q; R потенциальным? Если да,
найти его скалярный потенциал.
F 1 ; 1 ; 1x y z
1) ln x z ln y z ln x y c
2) ln |
xy |
ln |
xz |
ln |
xy 2 |
c |
|
z |
y |
z |
|||||
|
|
|
|
3) не является
#4) ln xyz c
5)xln y y ln z z ln x c
3.16.10.Является ли векторное поле F P;Q; R потенциальным? Если да,
найти его скалярный потенциал.
F xz2 ; yz2 ; x2 y2 zy
#1) 12 z2 x2 y2 c
2)12 x2 y2 z2 c
3)12 y2 x2 z2 c
4)не является
5)12 x2 y2 x2 z2 y2 z2 c
3.17. Теория
3.17.1. Двойной интеграл |
|
a x b |
, |
||
f x, y dxdy , где D – прямоугольник |
|||||
|
|
|
D |
c y d |
|
|
|
|
|
|
|
|
вычисляется по формуле: |
|
|
||
|
b |
d |
|
|
|
1) f x, y dxdy dy f |
x, y dx |
|
|
||
D |
a |
c |
|
|
|
|
b |
|
d |
|
|
2) f x, y dxdy f x, y dx dy |
|
|
|||
D |
a |
|
c |
|
|
|
b |
d |
|
|
|
#3) f x, y dxdy dx f x, y dy |
|
|
|||
D |
a |
c |
|
|
|
33
|
d |
|
|
b |
|
|
4) f x, y dxdy f |
x, y dy dx |
|
|
|||
D |
c |
|
|
a |
|
|
|
b |
|
|
d |
|
|
5) f x, y dxdy f |
x dx f y dy |
|
|
|||
D |
a |
|
|
c |
|
|
3.17.2. Двойной интеграл |
f x, y dxdy , где D – произвольная область, |
|||||
|
|
|
|
D |
|
|
ограниченная сверху - графиком y 2 x |
, а снизу – графиком |
|||||
y 1 x ,и прямыми x a , x b , вычисляется по формуле: |
||||||
|
b |
d |
|
|
|
|
1) f x, y dxdy dy f |
x, y dx |
|
|
|||
D |
a |
c |
|
|
|
|
|
b |
2 x |
|
|
|
|
2) f x, y dxdy dy |
|
f x, y dx |
|
|
||
D |
a |
1 x |
|
|
|
|
|
b |
2 |
x |
|
|
|
#3) f x, y dxdy dx |
f x, y dy |
|
|
|||
D |
a |
1 x |
|
|
|
|
|
b |
1 x |
|
|
||
4) f x, y dxdy dx |
|
f x, y dy |
|
|
||
D |
a |
2 x |
|
|
||
|
2 x |
b |
|
|
||
5) f x, y dxdy |
|
dx f x, y dy |
|
|
||
D |
1 x |
a |
|
|
||
3.17.3. Двойной интеграл |
f x, y dxdy , где D – произвольная область, |
|||||
|
|
|
|
D |
|
|
|
|
|
|
x r cos |
вычисляется по формуле: |
|
в полярной системе координат |
|
|||||
|
|
|
|
y r sin |
|
|
#1) f x, y dxdy f r cos ,r sin rdrd
|
D |
D |
2) |
f x, y dxdy f r cos ,r sin drd |
|
|
D |
D |
3) |
f x, y dxdy f r cos ,r sin r2drd |
|
|
D |
D |
4) |
f x, y dxdy f r cos ,r sin r2 sin drd |
|
|
D |
D |
5) |
f x, y dxdy f r cos ,r sin r sin drd |
|
|
D |
D |
34
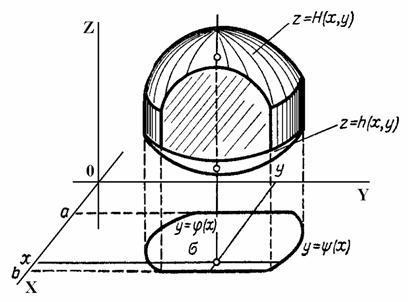
3.17.4.Для объемной области, представленной на рисунке, тройной интеграл вычисляется по формуле:
|
|
a |
(x) |
|
H x, y |
|
||
1) |
f x, y, z dxdydz dx |
|
dy |
|
|
f x, y, z dz |
||
|
V |
b x |
|
h x, y |
|
|||
|
|
|
b |
(x) |
|
H x, y |
||
#2) f x, y, z dxdydz dx |
dy |
|
f x, y, z dz |
|||||
|
V |
|
a x |
|
h x, y |
|
||
|
|
b |
(x) |
|
h x, y |
|
||
3) |
f x, y, z dxdydz dx |
|
dy |
|
|
f x, y, z dz |
||
|
V |
a x |
|
H x, y |
|
|||
|
|
b |
|
(x) |
|
H x, y |
|
|
4) |
f x, y, z dxdydz dx |
|
dy |
|
|
f x, y, z dz |
||
|
V |
a x |
|
h x, y |
|
|||
|
|
b |
|
(x) |
|
H x, y |
|
|
5) |
f x, y, z dxdydz dy |
|
dx |
|
|
f x, y, z dz |
||
|
V |
a x |
|
h x, y |
|
|||
3.17.5. Если в пространственной области (V) задана функция f x, y, z и
область (V) разбита с помощью сети поверхностей на конечное число областей V1,V2...,Vn , имеющих соответственно объемы V1, V2..., Vn , и в
каждой из областей Vi выбирается произвольно точка Mi xi , yi , zi , в которой вычисляются значения f Mi f xi , yi , zi , то тройным интегралом называется:
35

max Vi 0 |
f xi , yi , zi dVi |
||||||
1) |
lim |
|
|
|
|||
|
|
|
V |
|
|
|
|
|
|
|
|
n |
|
|
|
#2) |
lim |
|
f xi , yi , zi Vi |
||||
|
max Vi 0 |
i 1 |
|
|
|||
|
|
|
|
|
|
||
|
|
|
n |
n |
n |
xi , y j , zk Vi |
|
3) |
lim |
|
f |
||||
max Vi 0 |
i 1 |
j 1 |
k 1 |
|
|||
|
|
|
|
||||
|
|
|
n |
n |
n |
|
|
4) |
lim |
|
xi y j f xk , yk , zk zk |
||||
max Vi |
0 |
i 1 |
j 1 |
k 1 |
|||
|
|
|
|||||
|
|
|
n |
n |
n |
|
|
5) |
lim |
|
f |
xk , yk , zk zk |
|||
max Vi |
0 |
i 1 |
j 1 |
k 1 |
|
||
|
|
|
|
||||
3.17.6. Криволинейным интегралом первого рода f x, y dl называется
|
|
|
|
|
|
|
|
L |
|
|
|
n |
|
|
|
|
|
1) |
lim |
f |
xi , yi xi yi , где max li ; |
|||||
|
0 i 1 |
|
|
|
|
|
||
|
|
|
n |
|
|
|
|
|
#2) lim f xi , yi |
li ; |
|
|
|||||
|
0 i 1 |
|
|
|
|
|
||
|
|
|
n |
|
|
|
|
|
3) |
lim |
|
f xi , yi xi |
yi ; |
||||
|
0 i 1 |
|
|
|
|
|
||
|
|
|
n |
|
|
|
|
|
|
|
f |
xi , yi |
|
|
|
|
|
4) |
lim |
xi |
yi ; |
|||||
|
0 i 1 |
|
|
|
|
|
||
5) |
lim |
|
f x, y d |
|
|
|
|
|
|
0 |
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.17.7. Если кривая (L) задать параметрически, т.е. x t , y t t a,b , то криволинейный интеграл первого рода вычисляется
по формуле:
|
b |
|
|
1) f x, y dx f t , t dt ; |
|||
L |
a |
|
|
|
b |
|
|
|
|
|
|
#2) f x, y dx f t , t |
' t 2 ' t 2 dt ; |
||
L |
a |
|
|
36
|
b |
3) f x, y dx f t , t ' t dt |
|
L |
a |
|
b |
4) f x, y dx f t , t ' t dt |
|
L |
a |
|
b |
5) f x, y dx f t , t ' t ' t dt |
|
L |
a |
3.17.8. Если функции P x, y и Q x, y непрерывны в области (D), ограниченной контуром (L), то справедлива формула Грина:
#1) |
|
Q |
|
P |
Pdx Qdy |
|||
|
x |
|
y |
dxdy |
||||
|
D |
|
|
|
L |
|||
|
|
|
|
|
|
|
||
|
|
P |
|
Q |
|
|
||
2) |
x |
|
|
dxdy Pdx Qdy |
||||
D |
|
|
y |
L |
|
|||
|
|
|
|
|
|
|
||
|
|
Q |
|
P |
|
|
||
3) |
x |
|
|
dxdy Pdx Qdy |
||||
D |
|
|
y |
L |
|
|||
|
|
|
|
|
|
|
||
|
|
Q |
|
P |
|
|
||
4) |
y |
|
|
dxdy Pdx Qdy |
||||
D |
|
|
x |
L |
|
|||
|
|
|
|
|
|
|
||
|
|
Q |
|
P |
|
|
||
5) |
y |
|
|
dxdy Pdx Qdy |
||||
D |
|
|
x |
L |
|
|||
|
|
|
|
|
|
|
||
. |
|
|
Если кривая (L) задать параметрически, т.е. x t , y t |
|||||
3.17.9. |
||||||||
t a,b , то криволинейный интеграл второго рода вычисляется по формуле:
|
|
|
b |
|
|
|
|
|
|
1) P x, y dx Q x, y dy P t , t Q t , t ' t dt |
|
|
|||||||
|
L |
|
a |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
2) P x, y dx Q x, y dy P t , t ' t Q t , t dt |
|
|
|||||||
|
L |
|
a |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
P x, y dx Q x, y dy |
|
|
||||||
3) |
|
|
P |
t , t |
' t Q |
t , t ' |
t |
dt |
|
|
L |
|
a |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
4) P x, y dx Q x, y dy P t , t ' t Q t , t dt |
|
||||||||
|
L |
|
a |
|
|
|
|
|
|
37
|
|
|
|
|
|
b |
|
|
|
|
|
|
||
|
|
|
P x, y dx Q x, y dy |
|
|
|||||||||
#5) |
|
|
|
|
P t , t |
|
Q |
t , t ' t |
dt |
|||||
|
|
|
L |
|
|
a |
|
|
|
|
|
|
||
3.17.10. Если функция f P |
, P x, y, z непрерывна в замкнутой области |
|||||||||||||
|
|
|
|
|
|
|
объема V, то найдется точка Pc , такая, что будет справедлива |
|||||||
|
|
|
|
|
|
формула: |
|
|
|
|
|
|
|
|
#1) f P dv f Pc V |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2) |
|
|
1 |
|
|
f P dv f P V |
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|||||||
|
c |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
|
V f P dv f Pc |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) |
|
f P dv f Pc / V |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5) |
|
f P dv f Pc V |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.17.11.Тройной интеграл |
f x, y, z dxdydz , где V – произвольная область, |
|
|
|
V |
|
|
x r cos |
|
|
|
|
в цилиндрической системе координат y r sin вычисляется по |
|
|
|
|
|
|
z z |
|
формуле: |
|
1) f x, y, z dxdydz f r cos ,r sin , z d drdz |
||
V |
V |
|
2) |
f x, y, z dxdydz f r cos ,r sin , z r2drd dz |
|
V |
V |
|
3) |
f x, y, z dxdydz f r cos , r sin , z r sin drd dz |
|
V |
V |
|
#4) f x, y, z dxdydz f r cos ,r sin , z rdrd dz |
||
V |
V |
|
5) |
f x, y, z dxdydz f r cos ,r sin , z d drdz |
|
V |
V |
|
3.17.12. Тройной интеграл |
f x, y, z dxdydz , где V – произвольная |
|
|
|
V |
x cos sin
область, в сферической системе координат y sin sin
z cos
38
вычисляется по формуле:
1) f x, y, z dxdydz f ( cos sin , sin sin , cos )d d d ;
V V
2) f x, y, z dxdydz f ( cos sin , sin sin , cos ) d d d
V V
#3) f x, y, z dxdydz f ( cos sin , sin sin , cos ) 2 sin d d d
V |
|
V |
|
|
4) f x, y, z dxdydz |
f ( cos sin , sin sin , cos ) 2 cos d d d |
|||
V |
|
V |
|
|
5) f x, y, z dxdydz |
f ( cos sin , sin sin , cos ) sin d d d |
|||
V |
|
V |
|
|
3.7.13. Теорема Гаусса-Остроградского. |
|
|
||
Если в некоторой области G пространства 3 |
координаты вектора |
|
||
|
|
|
|
|
a P x, y, z i |
Q x, y, z j R x, y, z |
k |
|
|
|
|
|
P Q R |
|
непрерывны и имеют непрерывные частные производные x , y , z |
, то |
|||
поверхностный интеграл по любой замкнутой кусочно-гладкой поверхности S, лежащей в области G и ограничивающей область V, равен тройному интегралу:
|
|
|
|
|
P |
|
|
Q |
|
|
R |
|
||
1) |
Pdydz Qdzdx Rdxdy |
x |
|
y |
|
z |
dxdydz |
|||||||
|
S |
V |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
P |
|
|
|
Q |
|
|
|
R |
|||
2) |
Qdydz Pdzdx Rdxdy |
x |
|
|
|
y |
|
|
|
dxdydz |
||||
|
S |
V |
|
|
|
|
|
|
|
z |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3) Pdydz Rdzdx Qdxdy |
|
P |
|
Q |
|
R |
|
|||||||
|
x |
y |
|
dxdydz |
||||||||||
|
S |
V |
|
|
|
|
|
z |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4) Rdydz Pdzdx Qdxdy |
|
P |
|
Q |
|
R |
|
|||||||
|
x |
y |
|
dxdydz |
||||||||||
|
S |
V |
|
|
|
|
|
z |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
P |
|
Q |
|
R |
|
||||
#5) Pdydz Qdzdx Rdxdy |
x |
y |
z |
dxdydz |
||||||||||
|
S |
V |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3.7.14.Для того, чтобы криволинейный интеграл по любому замкнутому контуру L был равен нулю
Pdx Qdy 0
L
необходимо и достаточно выполнение равенства
39
1) P Q
x y
2)2 P 2Qx2 y2
#3) P Q
y x
4) 2 P 2Q
y2 x2
5)P Qx y
3.7.15. Для того, чтобы криволинейный интеграл Pdx Qdy не зависел от
L |
|
пути интегрирования L в области, в которой функции P x, y и |
Q x, y |
непрерывны вместе со своими частными производными, необходимо и достаточно выполнение равенства
1) P Q
x y
2)2 P 2Qx2 y2
#3) P Q
y x
4) 2 P 2Q
y2 x2
5) P Q
x y
3.7.16.Если функции P x, y, z , Q x, y, z , R x, y, z непрерывны вместе со
своими частными производными первого порядка в точках поверхности S, то имеет место формула Стокса
|
|
P |
|
Q |
|
R |
|
Q |
P |
|
R |
|
|
1) |
|
|
|
dxdy |
|
|
dydz |
|
|
dxdz Pdx Qdy Rdz |
|||
|
S |
y |
|
x |
|
y |
|
z |
|
z |
|
x |
L |
|
|
P |
|
Q |
|
Q |
|
R |
P |
|
R |
|
|
2) |
|
|
|
dxdy |
|
|
dydz |
|
|
dxdz Pdx Qdy Rdz |
|||
|
S |
y |
|
x |
|
z |
|
y |
|
z |
|
x |
L |
40
