

5)12
3.8.5.Вычислить поверхностный интеграл
xdydz , где |
S внутренняя сторона части параболоида |
x a2 |
y2 |
z2 , |
S |
|
|
|
|
отсеченная плоскостью Y 0Z . 1) a4 ;
#2) |
a4 |
|
|||
|
|
; |
|
||
|
2 |
|
|||
|
|
|
|
|
|
3) 0; |
|
|
|
|
|
4) |
a4 |
; |
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
5) a4 |
|
|
|
||
|
|
|
|
Теория поля |
|
|
|
|
|
3.9 Формула Грина. |
|
3.9.1 Вычислить интеграл по замкнутому контуру |
L : Pdx Qdy , при этом |
||||
L обозначает положительное направление |
обхода контура, а |
||||
L отрицательное. |
|
||||
(1 x2 ) ydx x(1 y2 )dy , где L окружность: x2 y2 1
L
1)2 ;
2)0;
3)4 ;
#4) 2 ; 5)
3.9.2. Вычислить интеграл по замкнутому контуру L : Pdx Qdy , при этом
L обозначает положительное направление обхода контура, аL отрицательное.
(2x y)dx 2 ydy , где L контур треугольника ABC с вершинами в точках
L
A(0; 1) , B(0;2) , C(2;0) .
1)6 ;
2)3 ;
3)0; #4) 3;
5)6
21

3.9.3. Вычислить интеграл по замкнутому контуру L : Pdx Qdy , при этом
L обозначает положительное |
направление обхода контура, а |
||
L отрицательное. |
|
||
|
xdy ydx |
( y 2)2 1 |
|
|
, где L окружность: x2 |
||
(x y)2 |
|||
L
1) 2 ;
2) ; #3) 0;
4);
5)2
3.9.4. Вычислить интеграл по замкнутому контуру L : Pdx Qdy , при этом
L обозначает положительное |
направление обхода контура, а |
|
L отрицательное. |
|
|
( y2 3x2 y)dx (xy x3 )dy , где |
L квадрат ABCD с вершинами A(0;0) , |
|
L |
|
|
B(0;2a) , C(2a;2a) , D(2a;0) . |
|
|
1) 0; |
|
|
2) |
2a3 ; |
|
#3) 4a3 ; |
|
|
4) |
6a3 ; |
|
5) |
8a3 |
|
3.9.5. Вычислить интеграл по замкнутому контуру L : Pdx Qdy , при этом
L обозначает положительное |
направление |
обхода контура, |
а |
|||||
L отрицательное. |
|
|
|
|
||||
(x2 2xy 3x)dy (2xy y2 |
y)dx , |
где L контур |
треугольника ABC |
с |
||||
L |
|
|
|
|
|
|
|
|
вершинами в точках A( a;0) , |
B(a;0) , |
C(0;a) . |
|
|
||||
1) |
|
a2 |
; |
|
|
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2) |
|
3a |
2 |
; |
|
|
|
|
|
|
|
|
|
|
|
||
|
4 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
3) a2 ; |
|
|
|
|
||||
4) |
|
3a |
2 |
; |
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
#5) 2a2 |
|
|
|
|
||||
3.10. Формула Стокса.
3.10.1. Вычислить циркуляцию векторного поля F Fdr в заданном
L
направлении обхода контура L .
22
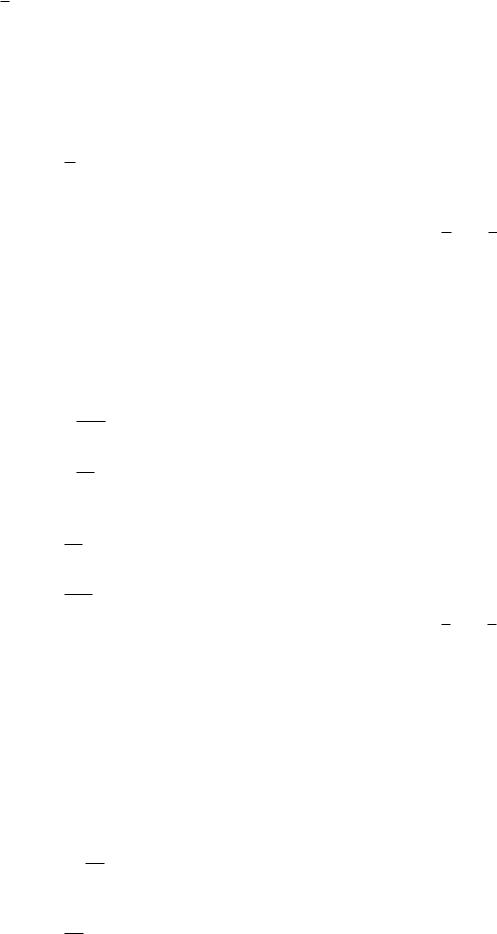
F yz; xz; xy 2y , L контур треугольника, образованного при пересечении плоскости x y z 1 с координатными плоскостями.
Направление обхода контура против часовой стрелки, если смотреть со стороны конца нормали, опущенной на плоскость из начала координат.
1) 1;
2) 0;
3) 12 ;
#4) 1; 5) 2
3.10.2. Вычислить циркуляцию векторного поля F Fdr в заданном
|
|
|
|
|
L |
направлении обхода контура L . |
|
|
|
||
|
|
xy;1; z , L окружность: |
x2 y2 |
a2 |
|
F |
. Направление обхода контура |
||||
|
|
|
z a |
|
|
против часовой стрелки, если смотреть со стороны положительного направления оси 0Z .
1)23a3 ;
2)a3 ; 3
#3) 0;
4)a3 ; 3
5)2a3
3
3.10.3 Вычислить циркуляцию векторного поля F Fdr в заданном
|
|
|
|
L |
|
|
направлении обхода контура L . |
|
|
|
|||
|
|
|
0 |
x a |
|
|
|
|
|
|
|
|
|
F yexy ; xexy ; xyz , контур L квадрат той грани куба |
y a , где |
y a . |
||||
0 |
||||||
|
|
|
|
z a |
|
|
|
|
|
0 |
|
||
Направление обхода контура против часовой стрелки, если смотреть со стороны положительного направления оси 0Y .
1) a4 ;
#2) a4 ; 2
3)0;
4)a4 ; 2
23

|
|
5) a4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3.10.4. Вычислить циркуляцию |
векторного |
|
поля |
F |
Fdr в заданном |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
||
направлении обхода контура L . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
2 |
y |
2 |
z |
2 |
4R |
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
F |
2x; xy |
2 ; z2 |
|
, L окружность: |
x |
|
|
|
|
|
направление обхода |
|||||||||
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
3R |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
контура |
|
L |
против часовой |
стрелки, если смотреть со стороны |
||||||||||||||||
положительного направления оси 0Z . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
#1) |
R4 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2)R4 ; 2
3)3 R4 ;
4
4)R4 ;
5)3 R4
2
|
|
|
|
|
|
|
|
||||
3.10.5.Вычислить циркуляцию векторного поля F |
Fdr в |
заданном |
|||||||||
|
|
|
|
|
|
|
|
L |
|
||
направлении обхода контура |
L . |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
F |
2xz y2 ;2xy; x2 |
2yz , |
L контур |
треугольника |
|
ABC с |
вершинами |
||||
A(0;0;0) , |
B(0;1;1) , |
C(0;2;0) . |
Направление |
|
обхода |
контура |
|||||
L : A C B A .
1)23 ;
2)13 ;
3)0;
4)13 ; #5) 23
3.11.Формула Остроградского-Гаусса.
3.11.1.Вычислить поток векторного поля F P;Q; R через внешнюю
поверхность тела S , замкнутую и кусочно-гладкую. (Fn)ds .
|
|
x; y; z , |
S |
|
|
S внешняя сторона поверхности пирамиды, ограниченной |
|
F |
|||
плоскостью x y z 2 и координатными плоскостями.
1)2;
2)3;
24

#3) 4;
4)6;
5)8
3.11.2.Вычислить поток векторного поля F P;Q; R через внешнюю
поверхность тела S , замкнутую и кусочно-гладкую. (Fn)ds .
S
F x3; y3; z3 , S внешняя сторона поверхности сферы x2 y2 z2 R2
1)6 R5 ;
5
2)8 R5 ;
5
3)9 R5 ;
5
|
|
|
|
|
|
|
12 R5 |
|
|
|
|
|
||||
|
|
|
|
#4) |
|
|
|
|
; |
|
|
|
|
|
||
|
|
|
|
5 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
5) |
16 R5 |
|
|
|
|
|
||||||
|
|
|
|
|
|
5 |
|
|
|
|
|
P;Q; R через внешнюю |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
||||||||||||
3.11.3. Вычислить |
поток векторного поля F |
|||||||||||||||
|
|
|
|
|
||||||||||||
поверхность тела S , замкнутую и кусочно-гладкую. (F |
n)ds . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
||
|
|
|
x2 y; xy2 |
|
|
S внешняя сторона поверхности тела, ограниченного |
||||||||||
F |
|
;2z , |
||||||||||||||
параболоидом z x2 |
y2 и плоскостью z 1. |
|||||||||||||||
1)4 ;
2)2 ;
3)34 ; #4) ;
5)5
4
3.11.4.Вычислить поток векторного поля F P;Q; R через внешнюю
поверхность тела S , замкнутую и кусочно-гладкую. (Fn)ds .
S
F x2 ; y2 ; z2 , S внешняя сторона поверхности куба, расположенного в
0 x a
первом октанте, с ребром, равным a : 0 y a .
0 z a
25

1)a4 ;
2)3a4 ;
2
3)2a4 ;
#4)3a4 ;
5)6a4
3.11.5.Вычислить поток векторного поля F P;Q; R через внешнюю
поверхность тела S , замкнутую и кусочно-гладкую. (Fn)ds .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
y |
2 |
z |
2 |
|
|
|
|
2x; 7 y; z , S внешняя сторона поверхности конуса x |
|
|
|
|
||||||||||||||||||||
F |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 1, z 0 |
|
|
|||||
|
|
1) |
8 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2) |
2 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
#3) |
4 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4) |
|
2 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5) |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3.12. Вычислить дивергенцию векторного поля |
a ax ;ay ;az |
в точке |
||||||||||||||||||||||||
M0 (x0 ; y0 ; z0 ) . |
|
|
|
|
|
|
|
a ax ;ay ;az |
|
|
|
|||||||||||||||
3.12.1. |
Вычислить |
дивергенцию |
векторного |
поля |
в |
точке |
||||||||||||||||||||
M0 (x0 ; y0 ; z0 ) . a x3 y xy2 ; xy3 x2 y; z3 M0 ( 2;1;1) |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
1) 1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2) |
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3) |
1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4) |
3; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
#5) 6; |
|
|
|
|
|
|
|
|
|
|
|
a ax ;ay ;az |
|
|
|
|||||||||||
3.12.2. |
Вычислить |
дивергенцию |
векторного |
поля |
в |
точке |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
|
|
|
|
|
|
|
|
|
|
|
M0 (x0 ; y0 ; z0 ) . a z ln |
|
; z ln |
|
; xy ln z M0 ( 2; |
2;4) |
|
|
|
|
|
|
|
|
|||||||||||||
y |
x |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1) 8 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2) |
6 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
#3) 3 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4) |
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5) |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
26
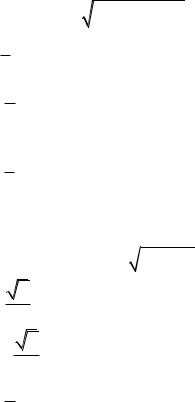
3.12.3. |
Вычислить |
дивергенцию |
векторного |
поля |
a ax ;ay ;az |
в |
точке |
||||||||||||||||||
M0 (x0 ; y0 ; z0 ) . a zarctg(x y); zarctg(x y); xyz M0 (1;1;5) |
|
|
|
|
|||||||||||||||||||||
|
|
1) 5 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
#2) 3 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
3) |
|
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
4) |
|
3; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
5) |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
a ax ;ay ;az |
|
|
|||||
3.12.4. |
Вычислить |
дивергенцию |
векторного |
поля |
в |
точке |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
y |
|
|
z |
|
|
|
|
|
|
M |
|
(x ; y ; z ) |
. a |
|
; |
|
|
; |
|
|
|
M |
|
( 1;0;1) |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
0 |
0 |
|
0 0 |
|
x2 y2 z2 |
|
x2 |
y2 z2 |
|
x2 |
y2 z2 |
0 |
|
|
|
|||||||||
|
|
1) |
|
|
|
1 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2) |
|
|
|
1 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
3) |
|
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
4) |
|
|
1 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
#5) |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3.13. Найти модуль градиента скалярного поля u f (x, y, z) в точке
M0 (x0 ; y0 ; z0 ) . |
|
|
|
|
||||
3.13.1. |
Найти модуль градиента |
|
скалярного поля u f (x, y, z) в точке |
|||||
|
|
|
|
|
|
|
||
M |
0 |
(x ; y ; z ) . u |
x2 y2 z2 , M |
0 |
(1; 2;2) |
|||
|
0 |
0 |
0 |
|
|
|
||
1)13 ;
2)23 ; #3) 1;
4)53 ;
5)3
3.13.2. Найти модуль градиента скалярного поля u f (x, y, z) в точке
M0 (x0 ; y0 ; z0 ) . u ln(x 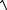
 y2 z2 ) , M0 (1;0; 1)
y2 z2 ) , M0 (1;0; 1)
1)  42 ;
42 ;
#2)  22 ; 3) 12 ;
22 ; 3) 12 ;
27
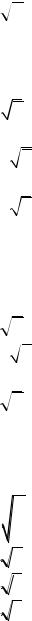
4)1;
5)
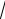 2
2
3.13.3. |
Найти |
модуль градиента скалярного поля u f (x, y, z) в точке |
||||||||
M |
|
(x ; y ; z ) . |
u xz2 |
|
y |
, M |
|
(2;2; 1) |
||
0 |
|
0 |
||||||||
|
0 |
0 |
0 |
|
|
z |
|
|||
|
|
|
|
|
|
|
|
|
||
1)
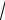 3 ;
3 ;
2)2;
#3) 
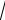 6 ;
6 ;
4)3;
5)2
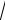 3
3
3.13.4. |
Найти |
модуль градиента скалярного поля u f (x, y, z) в точке |
||||||||
M |
|
(x ; y ; z ) . |
u |
1 |
x2 |
2arctg( y z) , M |
|
( 1;2;1) |
||
0 |
|
0 |
||||||||
|
0 |
0 |
0 |
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
1)1;
2)
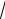 2 ;
2 ;
#3) 
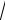 3 ;
3 ;
4)2;
5)
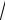 6 ;
6 ;
3.13.5. |
Найти |
модуль |
|
градиента |
скалярного поля u f (x, y, z) в точке |
||||||||||||
M0 (x0 ; y0 ; z0 ) . |
u ln |
yz |
, |
1 |
|
1 |
|
|
|||||||||
|
|
M0 |
|
; |
|
;1 |
|||||||||||
x |
|
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||
1) |
|
|
3 |
; |
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2) |
2 ; |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3) |
3 ; |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4) |
6 ; |
|
|
|
|
|
|
|
|
|
|
||||||
#5) 3
3.14.Вычислить ротор векторного поля a ax ;ay ;az в точке
M0 (x0 ; y0 ; z0 ) .
3.14.1.Вычислить ротор векторного поля a ax ;ay ;az в точке M0 (x0 ; y0 ; z0 ) .
axy2 ; x2 y; z(x2 y2 ) M0 (1; 1;2)
1)4; 4;0 ;
2)4; 4; 4 ;
3)4;4;0 ;
4)4;4;0 ;
#5) 4; 4;0
28

3.14.2. Вычислить ротор векторного поля a ax ;ay ;az в точке
|
xz |
|
yz |
|
xy |
|
||
M0 (x0 ; y0 ; z0 ) . |
a |
|
; |
|
; |
|
|
M0 ( 1;1; 1) |
|
|
|
||||||
|
y |
|
x |
|
z |
|
||
1)0;2;2 ;
2)2;2;0 ;
3)2;0;2 ;
#4) 2;0;2 ; 5) 2;0; 2
3.14,3.Вычислить ротор векторного поля a ax ;ay ;az в точке M0 (x0 ; y0 ; z0 ) .
a3y2 ; 3x2 ; z2 (x y) M0 (1; 2;1)
1)1;2; 6 ;
#2) 1; 1;6 ;
3)1; 2;6 ;
4)1;2;6 ;
5)2;1;6
3.14.4.Вычислить ротор векторного поля a ax ;ay ;az в точке M0 (x0 ; y0 ; z0 ) .
|
x |
|
z |
|
y |
|
1 |
|
1 |
|
|
a ln |
|
;ln |
|
;ln |
|
|
M0 |
|
; |
|
;1 |
|
|
|
|
|
|||||||
|
y |
|
x |
|
z |
4 |
|
2 |
|
||
1)1;0;2 ;
2)1;0;2 ;
3)1;2; 2 ;
4)1;2; 2 ;
#5) 1;0; 2
3.14.5.Вычислить ротор векторного поля a ax ;ay ;az в точке M0 (x0 ; y0 ; z0 ) .
zy |
|
xz |
|
xy |
|
|
1 |
|
|||||
a |
|
|
; |
|
|
; |
|
|
|
M |
0 |
|
;1;1 |
|
2 |
y |
2 |
z |
2 |
|
|||||||
x |
|
|
|
|
|
|
|
2 |
|
||||
1)3;0; 3 ;
2)0; 3;3 ;
#3) 0;3; 3 ;
4)3;0;3 ;
5)3;3;0
3.15.Является ли векторное поле F P;Q; R соленоидальным?
3.15.1.Является ли векторное поле F P;Q; R соленоидальным?
29
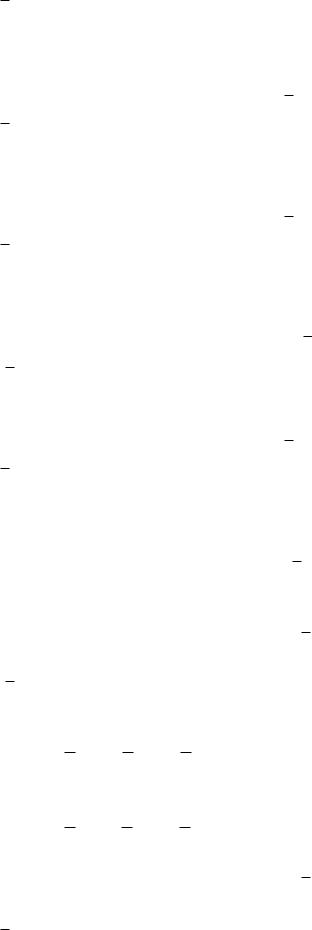
F x2 y;0; 2xyz
1)нет;
#2) да.
3.15.2.Является ли векторное поле F P;Q; R соленоидальным?
F 0; 2zx;0
1)нет;
#2)да
3.15.3. Является ли векторное поле F P;Q; R соленоидальным?
Fyz; zx; xy
1)нет;
#2) да;
3.15.4. Является ли векторное поле F P;Q; R соленоидальным?
F 3y2 ; 3x2 ; ( y2 2x)
1) нет;
#2)
3.15.5. Является ли векторное поле F P;Q; R соленоидальным?
F y z; x z; x y
1) нет;
#2) да.
3.16. Является ли векторное поле F P;Q; R потенциальным? Если да,
найти его скалярный потенциал.
3.16.1. Является ли векторное поле F P;Q; R потенциальным? Если да, найти его скалярный потенциал.
Fy z; x z; x y
1)нет;
2)12 x2 y 12 y2 z 12 z2 x c ;
3)x2 ( y z) y2 (x z) z2 (x y) c ;
4)12 xy2 12 yz2 12 zx2 c ;
#5) x( y z) yz c
3.16.2. Является ли векторное поле F P;Q; R потенциальным? Если да, найти его скалярный потенциал.
F 1; yz2 ; zy2
30
