Добавил:

Morze Developer Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский технический университет связи и информатики

Предмет:

Высшая математика

Файл:

Курсовая 2 часть

.pdf

Скачиваний:

160

Добавлен:

16.01.2023

Размер:

16.72 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 143 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

9. Вычислить криволинейный интеграл (циркуляцию)

5 y x dx y 2z dy 1 2 y z dz , где C линия, определяемая уравнениями

x 3cost; y 2sint; z 3cost 2sint; t 0; 2 (в направлении, соответствующем возрастанию параметра t ). Ответ: 30 .

Решение:

а). Непосредственно:

C :

x2	z2
		1

16	25

5x 10 y 6z 0

x2 3z dx 5 y

x 4cost

y 2cost 3sin t

z 5sin t, t 0;2

3 dy z 7x dz

dx 4sin t

dy 2sin t 3cos t dtdz 5cos tdt

16cos2 t 15sin t 4sin t dt 10cost 15sin t 3 2sin t 3cos t dt

C
	2	60sin2 t 30sin2 t 30cos2 t 140cos2 t dt
5sin t 28cost 5cost dt =		60sin2 t 30sin2 t 30cos2 t 140cos2 t dt
C	0
2	30 15 15 70 200 .

б). По формуле Стокса:

cos

3 cos 10cos

x2 3z

5y 3

z 7x

dxdz 10 ab 4 5 10 200 .

ПрXOZ

10. Найти дивергенцию и ротор векторного поля a ; выяснить, является ли данное поле потенциальным или соленоидальным; если да, то найти соответственно его скалярный или векторный потенциал и сделать проверку потенциала:

a ez i j x y k . diva x y ez , rota 0 ; поле потенциальное со скалярным потенциалом U x y ez C .

Вариант 5

1. Расставить пределы интегрирования двумя способами в двойном интегралеf x, y dxdy в декартовых координатах для области D : x2 = 2 y, x + y = 0.

		D
			2 x2
2			2 x2								1		2 y						2		2 y
dx f (x, y)dy dy																f (x, y)dx dy						f (x, y)dx
1				x					2				y						1
1				x					2				y						1		2 y
2. Найти массу неоднородной пластины D : x 0,																											y 1,					y x, если поверхностная
плотность в каждой ее точке x, y x2																					2y2.					712				m x, y dxdy
																																		D
3. Найти статический момент однородной пластины																													D :				x2 y2 2x 0,
x2 y2 2y 0,								x 0,					относительно оси Ox , используя																				полярные координаты.									1	2
x2 y2 2y 0,								x 0,					относительно оси Ox , используя																				полярные координаты.								2		3
															4 4,											4												2			2		3
															4 4,											4							2a cos					2


M x			sin d d												a cos 2a cos												sind										d
				D											a cos 2a cos
				D																													a cos
																										4
																										4
4. Найти координаты центра масс однородного тела, занимающего область V :
z 5 x2 y2 , x2 y2 2, z 0.																		0,0,10 3
Данное тело симметрично относительно оси Oy Ox,Oz , поэтому xc																																								yc 0, а
				z x, y, z dxdydz
z				V										.
z					x, y, z dxdydz									.
	c				x, y, z dxdydz
	c
				V
Переходя к цилиндрическим координатам по формулам:																																	x cos ,							y sin ,	z z,
имеем:
																2		4		8					1	2			4				64 4 2 d
zdxdydz z d d dy d																			d zdz						1	d
zdxdydz z d d dy d																			d zdz						2	d
V							V									0		0		2						0			0
		1				2					4				512 256 256
		1				2					4		4
			2		64			4					0
		2	2		64	2		4			4
		2				2					4
																2	4		8								2					2 3			2				4
dxdydz d d dy d																	d dz 2									8										d 8 2 d
dxdydz d d dy d																	d dz 2									8	2						3			d 8 2 d
V						V										0	0		2								2						3		0				0
					2		2 3			4						4				128								64					128
					2		2 3			4						4				128								64					128
2 4											0					2			64				2														.
2 4						3										2			64				2					3						3			.
						3										0					3							3						3
																0					3
Следовательно,								yc			zdxdydz / dxdydz													256 3						768					12			6 и центр масс
Следовательно,								yc			zdxdydz / dxdydz													128							128						2	6 и центр масс
												V						V						128							128						2
												V						V
C 0,0,6 .

5.	Найти момент инерции однородного тела относительно оси Ox , занимающего
область V : x2 y2 z2 ,		x 2. 16
		5
6.	Найти объем тела, ограниченного поверхностями: z2 4x,		x y 2,	y 0 .	64
					64	2
					15	2
					15
		z2 4x; x y 2; y 0;

		2		2 x		4			2
V 2	4xdxdy 4		xdx		dy 4			x			2
							x			x		x

D	0		0			3			5

1564 2

7. Вычислить непосредственно и с помощью формулы Грина: xydx 2xy2dy , где L

контур треугольника ABC : A 1;0 , B 0;1 , C 0;0 . 0

8. Вычислите поток векторного поля F x2i zj xyk через внешнюю сторону гра-

ницы области, ограниченной поверхностями z xy , x y 1 и z 0 . 1 30

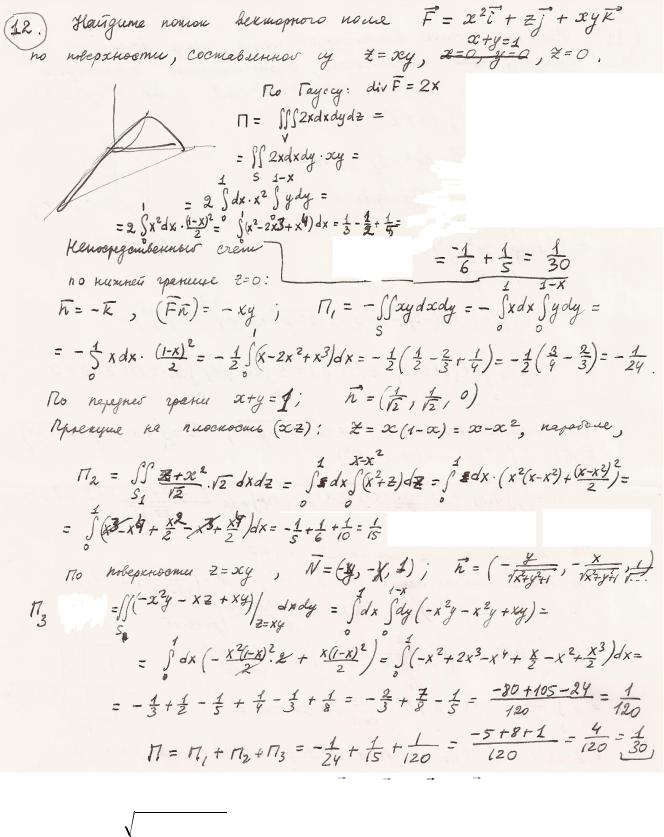
9. Найдите циркуляцию векторного поля F xzi z2 j yzk по линии пересечения полусферы z 2x x2 y2 и цилиндра x2 y2 x . 8

10. Найти дивергенцию и ротор векторного поля a ; выяснить, является ли данное поле потенциальным или соленоидальным; если да, то найти соответственно его скалярный

или векторный потенциал и сделать проверку потенциала: a y xi zk .

rota zi xk , diva 0 ; поле соленоидальное с векторным потенциалом

A xyz j gradФ .

Вариант 6

1. Расставить пределы интегрирования двумя способами в двойном интегралеf x, y dxdy в декартовых координатах для области D : y = 2 x2 , y = x2.

2 y2

2 x2

f (x, y)dy dy

f (x, y)dx dy

f (x, y)dx

2 y2

2. Найти массу неоднородной пластины D : x2 y2

1, если поверхностная плотность в

каждой ее точке x, y 2 x y. 2

m x, y dxdy

3. Найти статический момент однородной пластины D : x2 y2

2y 0,

x2 y2 2x 0, y 0, относительно оси Oy , используя полярные координаты.

4 4,

2a cos

M y

cos d d

a cos 2a cos

cosd

a cos

4. Найти координаты центра масс однородного тела, занимающего область V :

,0,0

x 6

2 z2 , y2 z2 9,

x 0.

Данное тело симметрично относительно оси Ox , поэтому yc zc 0, а

x x, y, z dxdydz

x, y, z dxdydz

Переходя к цилиндрическим координатам по формулам: x x,

z sin, y cos ,

имеем:

											2				6 2				2
											2		3		6 2			1	2	3
xdxdydz x d d dy d d																xdx		1	d 36 4d
xdxdydz x d d dy d d																xdx			d 36 4d
V					V		0						0		0		2		0	0
2			6
2			6				3 d 3 27 2 162 .
18
18					0
0		6			0
											2			6 2			2
											2	3		6 2			2		3
dxdydz d d dy d													d		dx 6 d 6 2d
V					V		0					0	0				0		0
2		4
2		4				3 d				3
6										3	2 9	27 .
6											2 9	27 .
0	4			0			2
Следовательно,						xc		xdxdydz / dxdydz									162		6.	и центр масс C 6,0,0 .
Следовательно,						xc		xdxdydz / dxdydz									27		6.	и центр масс C 6,0,0 .
									V				V				27
									V				V

5.	Найти момент инерции однородного тела относительно оси									Oy , занимающего
область		V :	y x2 z2 ,			y 2. 4
								3
6.	Найти объем тела, ограниченного поверхностями: z x2 y2 ,									z 2x .
											2

	2	2 cos		2 cos			8	2
V 2 d			d		dz		8	cos4 d
V 2 d			d		dz			cos4 d
	0	0		2		3		0	2

7. Вычислить непосредственно и с помощью формулы Грина: x2 y2 dx 2xydy , где

L контур треугольника ABC : A 1;1 , B 3;1 , C 3;2 . 163

8. Вычислите поток векторного поля F xzi yzj z2 k через внешнюю сторону

границы области, ограниченной поверхностями z 4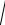25 x2 y2 и z 2 . 7

9. Вычислить криволинейный интеграл (циркуляцию)

12z 6x dx 3z2dy 6zy 18x dz , где C линия, определяемая уравнениями

x 3cost; y 6cost 4sint 1; z 4sint; t 0; 2 (в направлении, соответствующем возрастанию параметра t ). Ответ: ─ 360 .

Решение:

а). Непосредственно:

	x2		z2		x 4cost		dx 4sin t
				1		2cost 3sin t
				1
C :	16		25		y		dy 2sin t 3cos t dt
		10 y 6z 0				5sin t, t 0;2
	5x	10 y 6z 0			z	5sin t, t 0;2	dz 5cos tdt
I x2 3z dx 5 y 3 dy z 7x dz
	C
16cos2 t 15sin t 4sin t dt 10cost 15sin t 3 2sin t 3cos t dt
C
						2
5sin t 28cost 5cost dt = 60sin2 t 30sin2 t 30cos2 t 140cos2 t dt
C	30 15 15 70 200 .					0
2	30 15 15 70 200 .

<<< < Предыдущая 1 23 / 143 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в папке СИДЗ

#
16.01.202316.72 Mб160Курсовая 2 часть.pdf
#
16.01.2023950.34 Кб148Сидз 2.pdf