
будет непрерывной? |
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. Очевидно, что функция |
f x |
непрерывна при x 0 и при x 0, а |
|||||||||||||
так как f 0 1, f |
0 |
a , f 0 |
a , то функция f x будет непрерывной |
||||||||||||
и в точке x 0, если a 1. |
|
|
|
|
|
|
|
|
|||||||
5.4.4. Исследовать на непрерывность функцию |
|
|
|
||||||||||||
|
|
|
|
|
|
|
0,2 2x2 3 , |
x 1, |
|
|
|||||
|
|
|
|
|
|
|
|
5x, |
1 x 3 |
|
|
|
|
||
|
|
|
|
f x 6 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
3 , |
3 x |
|
|
|
|
||
|
|
|
|
|
|
|
x |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. На интервалах ,1 , 1,3 |
и 3, |
функция непрерывна. Поэтому |
|||||||||||||
разрывы возможны |
только |
в точках |
x 1и |
x 3, в |
которых |
изменяется |
|||||||||
аналитическое |
1 |
|
задание |
функции. |
В |
|
точке |
x 1 |
имеем: |
||||||
f 1 0 lim |
|
2x2 |
3 |
|
1, |
f 1 0 lim 6 5x 1, поэтому в точке x 0 |
|||||||||
x 1 0 |
5 |
|
|
|
|
|
x 1 0 |
|
f 3 0 |
lim 6 5x 9 и |
|||||
функция непрерывна. Рассмотрим точку x 3: |
|||||||||||||||
f 3 0 lim |
|
x 3 0, поэтому в точке x 3 |
|
x 3 0 |
|
||||||||||
|
функция терпит разрыв пер- |
||||||||||||||
x 3 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вого рода (односторонние пределы в точке x 3конечны, но не равны между
собой). |
Скачок |
функции |
в |
точке |
разрыва |
|
|
x 3 |
равен |
|||
f 3 0 f 3 0 0 9 9. |
|
|
|
|
|
|
|
|
|
|||
5.4.5. Исследовать на непрерывность функцию |
|
x |
, |
|
x 0, |
|
||||||
f (x) 4 3 |
|
|
|
|||||||||
Решение. Так как f 0 4, а f |
|
|
2a x, |
x 0 |
|
|||||||
0 2a , то равенство |
|
|
|
|
|
|
||||||
f 0 |
f 0 f 0 |
будет выполнено, если положить |
2a 4, т.е. a 2. |
|||||||||
5.4.6. |
При каком значении числа а функция f |
x |
a, |
|
|
x 5, |
|
|||||
(x) |
3x, |
|
x 5 |
|
||||||||
|
|
|
|
|
|
x2 |
|
|
||||
будет непрерывной?
Решение. Областью определения функции является все множество действительных чисел, причем по обе стороны точки х = 5 функция является элементарной, то есть непрерывной. Для обеспечения непрерывности в точке х = 5 поставим условие 5 a 25 15 a 5.
5.4.7. Каким числом можно доопределить функцию f (x) sin3x |
при х = 0, |
x |
|
чтобы она стала непрерывной в этой точке? |
|
41 |
|

Решение. Найдем предел данной функции в точке х = 0: limsin3x 3
x 0 x
если принять f (0) = 3, функция станет непрерывной точке х = 0.
5.4.8. Каким числом можно доопределить функцию |
f (x) xsin |
x2 |
3x 2 |
|
|||||||||||
|
x |
||||||||||||||
при х = 0, чтобы она стала непрерывной в этой точке? |
|
||||||||||||||
|
|
|
|||||||||||||
При |
|
x 0 |
|
limx 0 x б.м., |
|
|
|
|
|
||||||
Решение. |
|
|
|
|
|
|
x 0 |
|
|
|
ограниченная функция. |
||||
|
|
2 |
3x 2 |
|
|
x |
2 |
3x 2 |
|
||||||
|
|
|
|
||||||||||||
|
|
sin |
x |
|
|
1 sin |
|
|
|
|
|
|
|||
|
|
x |
|
|
x |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Как известно, произведение бесконечно малой функции на ограниченную есть
|
|
2 |
3x 2 |
|
|
|
|
||||
бесконечно малая, поэтому |
lim xsin |
x |
|
0, то есть предел суще- |
|
|
|
x |
|||
|
x 0 |
|
|
||
ствует и конечен. Поэтому можно доопределить функцию так: f (0) = 0. |
|||||
5.4.9. Каким числом можно доопределить функцию f (x) arcctg 3 при х = 0, |
|||||
x
чтобы она стала непрерывной в этой точке? Решение.
у
π
y = arcctgx
х
Рис. 5.1
Найдем односторонние пределы данной функции в точке х = 0:
lim arcctg |
3 |
lim arcctgt |
|
3 |
|
, |
|
|
x |
t |
x |
|
|
||||
x 0 |
|
t |
|
|
|
|
||
lim arcctg |
3 |
lim arcctgt 0 lim arcctg |
3. |
|||||
x 0 |
x |
|
t |
x 0 |
|
|
|
x |
Следовательно, предел данной функции в точке х = 0 в обычном смысле не существует, поэтому добиться ее непрерывности в этой точке невозможно.
5.4.10. Определить значения параметров s и t , при которых функция
42

x, |
|
|
x |
|
|
1, |
|
|
|
|
|||||
f x |
|
|
|
|
|
|
непрерывна на R. |
|
|
|
|
|
|
||
x2 sx t, |
|
|
x |
1 |
|
||
|
|
|
|
|
|
|
|
Решение. Функция f x непрерывна в точке a , если предел справа равен пре-
делу |
слева |
и |
равен |
значению |
функции |
в |
этой |
точке: |
lim |
f x lim |
f x f a . |
Данная функция неэлементарная и |
на трех |
||||
x a 0 |
x a 0 |
|
|
|
|
|
|
|
интервалах меняет свое аналитическое выражение: при x 1 ( 1 x 1) задана функция вида x , на интервалах x 1 (x 1 и x 1) функция имеет вид x2 sx t (см. схему на рис. 5.1).
Рис. 5.2
Вычислим односторонние пределы: lim x2 sx t 1 s t ,
x 1 0
lim x 1, |
lim x 1, |
lim |
|
x2 sx t |
|
1 s t . |
x 1 0 |
x 1 0 |
x 1 0 |
|
|
Так как для непрерывной функции выполняются условия
lim |
|
x2 sx t |
|
lim |
x и lim |
|
x2 sx t |
|
lim x , |
x 1 0 |
|
x 1 0 |
x 1 0 |
|
x 1 0 |
то, приравнивая значения односторонних пределов, получим систему
1 s t 1, |
решив которую получим s 1, t 1. |
|||||
|
s t 1, |
|||||
1 |
|
|
|
|
|
|
|
|
5.5. Задачи для самостоятельного решения |
||||
|
5.5.1. Функция |
f x |
x2 |
9 |
не определена при x 3. Как следует |
|
|
x2 |
|
||||
|
|
|
|
3 |
||
доопределить функцию в точке x 3, чтобы она стала непрерывной?
5.5.2.Функция f x arctg x 1 1 не определена при x 1. Можно ли доопределить функцию в точке x 1 так, чтобы она стала непрерывной?
5.5.3.Подобрать числа a и b такие, чтобы функция f x была непрерывной, если:
43

|
|
|
|
|
|
|
|
x 1 3 , |
x 0, |
а) |
|
2 |
ax, |
0 x 1, |
, |
|
|
0 x 1, |
|
f (x) x |
|
б) f (x) ax b, |
|||||||
|
|
2 bx, |
1 x 2 |
|
|
x, |
x 1. |
||
|
|
|
|
|
|
|
|
||
5.5.4. Функция |
f x не определена при x 0. Определить значение |
||||||||
|
f 0 |
так, чтобы функция стала непрерывной при x 0, если: |
|||||||
а) |
f (x) |
|
1 |
x 1 |
, |
б) |
f (x) arcsinx |
|
|
|
3 1 |
|
|
|
|||||
|
|
|
x 1 |
|
2tgx |
|
|
||
Ответы. |
|
5.5.1. y 3 6. |
5.5.2. нет. 5.5.3. а) a 0, |
b 1. |
б)a 2, |
||||
b 1 |
5.5.4. а) |
f 0 3/ 2. |
б) |
f 0 1/2. |
|
|
|||
ЗАНЯТИЕ 6.
6. ТОЧКИ РАЗРЫВА 6.1.Точки разрыва и их классификация
Определение 6.1.1. Точка разрыва x0 называется точкой устранимого разрыва, если существуют односторонние пределы f (x0 0), f (x0 0) и они
равны между собой (т.е. lim f (x)).
x x0
Определение 6.1.2. Точка разрыва x0 называется точкой разрыва первого
рода (иногда применяется термин «скачок»), если существуют односторонние пределы f (x0 0), f (x0 0), но они не равны между собой.
Определение 6.1.3. Точка разрыва x0 называется точкой разрыва второго рода, если хотя бы один из односторонних пределов f (x0 0), f (x0 0) не существует (в частности, он может быть бесконечным).
6.2. Решение некоторых типовых задач, рассматриваемых в аудитории
6.2.1. Исследовать на непрерывность функцию y |
x2 |
3x 2 |
. |
|
x 1 |
||
|
|
|
44

у
1 х
х
Рис. 6.1
Решение. Функция не определена при x 1, а для остальных значений аргумента может быть представлена как y x 2. Следовательно,
lim |
x2 |
3x 2 |
1 |
2 |
1, |
|
x 1 |
||||
x 1 |
|
|
|
|
|
то есть x 1 – устранимая особенность. |
|||||
6.2.2. Исследовать на непрерывность функцию y | xx |. Решение.
у
1
х
 -1
-1
Рис. 6.2
Решение. Из определения модуля следует, что у = 1 при x > 0, y = -1 при x < 0, а при х = 0 функция не определена. При этом
lim |
| x | 1, |
lim |
| x | 1. |
|
|
||
x 0 |
x |
x 0 |
x |
|
|
|
|
Следовательно, х = 0 –точка разрыва 1-го рода. |
|
1 |
|
||||
6.2.3. Исследовать на непрерывность функцию |
y |
. |
|||||
|
|||||||
|
|
|
|
|
x2 |
||
45

у
х
Рис. 6.3
Решение. Функция не определена при x 0 , и
lim x12 .
x 0
Поэтому x 0 – точка разрыва 2-го рода.
1
6.2.4. Исследовать на непрерывность функцию y ex .
у
х
Рис. 6.4
|
1 |
|
1 |
|
Решение. |
limex |
0, |
limex |
, |
|
x 0 |
|
x 0 |
|
то есть правосторонний предел не является конечным. Значит, x 0 – точка разрыва 2-го рода.
6.2.5. Исследовать на непрерывность функцию |
y sin |
1. |
|
|
x |
46

у
х
Рис. 6.5
Решение. Функция не определена при x 0 и не имеет предела при x 0. Следовательно, x 0 – точка разрыва 2-го рода.
6.2.6. Найти количество точек разрыва функции |
y |
2x 3 |
. |
|
log2 | x | |
||||
|
|
|
Решение. Функция не существует при трех значениях аргумента: х = 0 (знаменатель не существует) и х = +1 (он равен 0). Все три точки являются внутренними точками области определения и, поэтому, точками разрыва.
Исследуем характер точек разрыва:
1) |
lim |
2x 3 |
lim(2x 3) lim |
|
1 |
3 0 |
0. |
|
|||
log2 | x | |
|
|
|
||||||||
|
x 0 |
x 0 |
x 0 log2 | x | |
|
|
|
|
||||
Следовательно, х = 0 – устранимая особенность. |
|
||||||||||
2) |
При x 1 | x | 1 log2 |
| x | 0 |
|
1 |
. |
||||||
log2 | x | |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
Следовательно, lim 2x 3 , и х = +1 – точки разрыва 2-го рода x 1 log2 | x |
3 точки разрыва. |
|
|
|
|
|
|
|
|
|
|
6.2.7. Среди |
функций |
1) f (x) cosx |
,2) |
f (x) |
|
5 |
,3) f (x) |
1 |
|
, |
|
1 |
(x |
5)2 |
|||||||
|
|
x |
|
1 |
|
|
||||
4) f (x) |2x 1| |
|
|
|
3x |
|
|
|
|
||
точки разрыва 1-го рода имеют? |
|
|
|
|
|
|||||
2x 1 |
|
|
|
|
|
|
|
|
|
|
Решение. Найдем точки разрыва каждой функции и исследуем их характер.
47
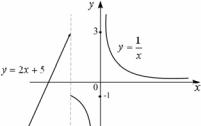
1) |
Функция |
|
|
|
f (x) cosx |
не |
|
определена |
при х |
= 0. |
|||||||||||||||||||||
limcosx |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
limcosx lim |
|
, |
следовательно, |
единственная |
точка |
разрыва |
|||||||||||||||||||||||||
x 0 |
x |
|
x 0 |
|
x 0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
этой функции – это точка разрыва 2-го рода. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
2) Функция |
f (x) |
|
|
|
5 |
|
|
|
не определена при х = 0 (заметим, что знаменатель |
||||||||||||||||||||||
|
|
|
|
|
1 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
1 3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
основной дроби не равен нулю ни при каком значении х). |
|
|
|
|
|
||||||||||||||||||||||||||
Найдем односторонние пределы f (x) в точке х = 0: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
lim |
5 |
|
|
5 |
|
|
|
5 |
|
|
|
5; |
lim |
5 |
|
|
5 |
|
|
|
5 |
0 |
5. |
|
|
||||||
|
|
1 3 |
|
|
|
|
|
|
|
|
1 3 |
|
|
|
|||||||||||||||||
x 01 31x |
|
|
|
|
1 |
0 |
|
|
|
x 01 31x |
|
|
|
|
|
|
|
|
|||||||||||||
Следовательно, х = 0 – точка разрыва 1-го рода. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
3) Функция |
f (x) |
|
|
|
1 |
|
|
|
|
не определена при х = 5. lim |
|
1 |
|
|
, |
|
|||||||||||||||
(x 5)2 |
|
|
5)2 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 5 (x |
|
|
|
|||||||||||||
следовательно, точка х = 5 – точка разрыва 2-го рода. |
|
|
|
|
|
||||||||||||||||||||||||||
4) Функция |
f (x) |
|2x 1| |
не определена при х = -0,5. При этом |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
2x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
f (x) |
|
2x 1 1, |
x 0,5 и = |
2x 1 1,x 0,5. |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
2x 1 |
|
|
|
|
|
2x 1 |
|
|
|
|
|
|
|
|
||||||||||
Таким образом, односторонние пределы в точке х = -0,5 равны соответственно 1 и -1, то есть эта точка – точка разрыва 1-го рода
2,4.
6.2.8.Найти точки разрыва функции
2x f x 1x
и определить их характер.
5 |
при x 1, |
при 1 x
Рис. 6.6
Решение. Неэлементарная функция f x определена на всей числовой оси, кроме точки x 0 (Рис. 6.6).
48
Так как f 0 lim f x |
lim |
1 , f 0 lim f |
x lim |
1 , |
|||||||||||||||||
то в точке x 0 |
x 0 |
|
x 0 |
x |
|
|
|
|
|
|
|
|
x 0 |
x 0 |
x |
||||||
функция терпит разрыв второго рода. Исследуем поведение |
|||||||||||||||||||||
функции в точках, где меняется аналитическое выражение функции: |
|
||||||||||||||||||||
f 1 0 lim |
f x lim |
|
2x 5 |
3, |
f 1 0 lim |
f x lim |
1 1. |
||||||||||||||
x 1 0 |
x 1 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 0 |
x 1 0 |
x |
||||
Найденные односторонние пределы функции конечны, но не равны между |
|||||||||||||||||||||
собой, поэтому в точке x 1 |
функция имеет разрыв первого рода. Скачок |
||||||||||||||||||||
функции в точке разрыва равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
f 1 0 f 1 0 lim |
f |
x |
|
lim f x 4. |
|
|
|||||||||||||||
|
x 1 0 |
|
|
|
|
x 1 0 |
|
|
|
|
|
|
|||||||||
6.2.9. Найти точки разрыва функции |
f x |
|
|
x a |
|
|
и определить их характер. |
||||||||||||||
|
|
||||||||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x a |
|
|
||||
Решение. Функция f x |
|
|
|
x |
a |
|
|
|
1, |
x a, |
следовательно, функция f x |
||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
x a, |
||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
x |
a |
|
|
|||||||||||||||
|
|
|
|
|
|
|
1, |
|
|
|
|
|
|
||||||||
определена и непрерывна на всей числовой оси, кроме точки x a . Так как |
|||
f a 0 |
lim f x 1, |
f a 0 lim f x 1, то в точке |
x a функция |
|
x a 0 |
x a 0 |
|
имеет разрыв первого рода. Скачок функции в точке разрыва x a равен |
|||
f a 0 |
f a 0 lim |
f x lim f x 1 1 2. |
|
|
x a 0 |
x a 0 |
|
6.2.10. Функция задается различными аналитическими выражениями для различных областей независимой переменной. Требуется:
1) найти точки разрыва функции, если они существуют;
2) найти скачок функции в каждой точке разрыва;
3) сделать схематический чертеж.
x 1, x 0,
y x2 1,0 x 1,
2,x 1.
Решение. Функция y1 x 1 непрерывна для x 0, функция y2 x2 1 непрерывна в каждой точке из 0,1 , функция y 3 2 непрерывна в каждой точке интервала 1, . Точки, в которых функция может иметь разрыв, это точки x 0 и x 1, где функция меняет свое аналитическое выражение.
49

Исследуем точку x 0: lim |
y lim |
x 1 1, |
lim y lim |
x2 1 |
1, |
||||
x 0 0 |
x 0 0 |
|
|
x 0 0 |
x 0 0 |
|
|
||
y 0 1 точка x 0 есть точка непрерывности функции |
y x . |
|
|||||||
Исследуем точку x 1: lim y lim |
|
x2 |
1 0, |
lim y lim |
2 2, |
y 1 0. |
|||
x 1 0 |
x 1 0 |
|
|
x 1 0 |
x 1 0 |
|
|
|
|
Таким образом, односторонние пределы существуют, конечны, но не равны между собой. По определению, исследуемая точка – точка разрыва первого рода. Величина скачка функции в точке разрыва x 1 равен
d lim y lim y 2 0 2.
x 1 0 x 1 0
Сделаем схематический чертеж
Рис. 6.7
6.3. Задачи для самостоятельного решения
Найти точки разрыва функции и установить их характер:
6.6.1. f x |
sinx |
. |
6.3.2. f x cosx . |
6.3.3. f x |
1 |
. |
|
|
|
||||||
|
x |
x |
|
lg |
x |
|
|
|
x |
|
x |
|
|
, x 0, |
|
|
|
|
|
|
|
||||
6.3.4. |
|
|
|
|
|
|
. |
|
|
|
|
|
|||||
x |
|
|
||||||
f x |
|
|
|
|||||
|
|
2, |
|
|
x 0. |
|
||
|
|
|
|
|
||||
6.3.7. f x xx32 279 .
1
|
f x |
2 |
x |
1 |
|
|
|
2 |
|
|||
6.6.5. |
. |
|
6.3.6. f x 3 |
|
. |
|||||||
|
1 x |
|||||||||||
|
|
1 |
|
|
|
|||||||
|
|
2x |
1 |
|
|
|
|
|
||||
|
|
|
1 |
, |
|
|
x 0, |
|||||
|
|
|
|
|
|
|||||||
|
x |
2 |
|
|
||||||||
6.3.8. |
|
|
|
|
|
2 |
,0 |
x 1,. |
||||
f x x 2 |
|
|||||||||||
|
2 x, |
|
|
x 1. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
50
