
Вариант 28
1. |
Вычислить пределы с помощью правила Лопиталя: |
|
|
|
|
||||||||||||
|
|
|
tgx 2 / |
|
2x |
|
|
|
|
cos x |
|
ln 2x 1 |
|
|
|
|
|
|
|
; б) |
|
. |
|
|
|
|
|||||||||
|
а) lim |
|
|
lim |
|
|
|
|
|
|
|||||||
|
x |
2 |
|
|
|
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Провести исследование и построить график функции y |
18 |
x 2 2 |
. |
|||||||||||||
|
|
x3 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
Построить график функции в полярной системе координат r 2sin 3 . |
||||||||||||||||
4.Найти основание a и боковую сторону b равнобедренного треугольника, вписанного в окружность единичного радиуса и имеющего среди всех таких треугольников наибольшую площадь.
5. |
Вычислить y |
28 |
функции |
y |
3 |
2x2 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
||
|
2x2 |
3x |
2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
6. |
Оценить с помощью формулы Тейлора абсолютную погрешность |
|
|||||||||||||||||||
|
приближенной формулы: |
1 x |
1 |
x |
|
|
|
x2 |
|
|
x3 |
,0 x 0,2 . |
|
|
|
|
|||||
|
2 |
|
8 |
16 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
t |
|
|
|
7. |
Составить уравнения касательной и нормали к кривой |
x |
|
в точке |
t0 1 |
||||||||||||||||
|
22t |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и вычислить yxx x0 .
8.Вычислить производную 2-го порядка от неявной функции: x y ex y .
9. Вычислить предел с помощью формулы Тейлора: lim |
1 2tgx ex x2 |
. |
||
arcsin x sin x |
||||
|
x 0 |
|
||
10. |
Применима ли теорема Ролля к функции f x 3 x2 |
3x 2 на отрезке 1;2 ? |
||
|
Если да, то найти c . |
|
|
|
11. |
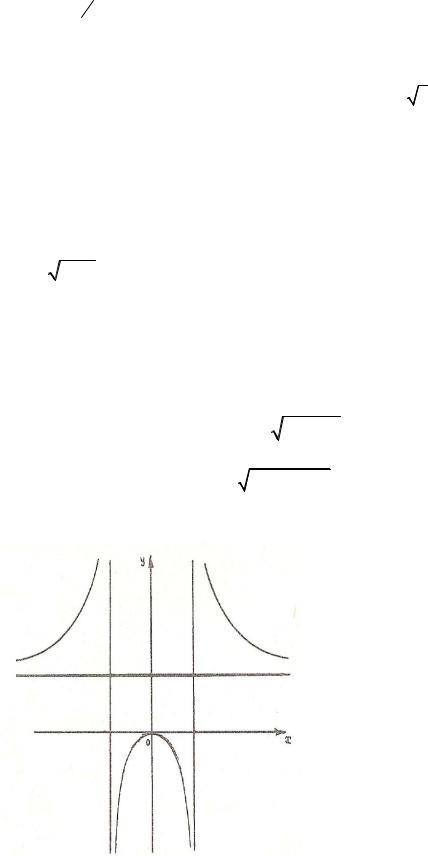
По графику функции построить график ее первой производной |
|
||
31
Вариант 29
1. Вычислить пределы с помощью правила Лопиталя: |
|||||||
|
2arctgx ln x ; б) |
|
|
1 |
1 / |
1 ln x |
|
а) lim |
lim |
|
|
|
|
. |
|
|
2 |
||||||
x |
|
x 0 |
x |
|
|
|
|
2. |
Провести исследование и построить график функции y |
e2 x |
. |
|
|||||
2 |
x |
|
|||||||
|
|
|
|
|
|
|
|
||
3. |
Построить график функции в полярной системе координат |
r |
1 2sin 2 |
||||||
4. |
На правой ветви квадратичной гиперболы |
y |
4 2 |
, |
x 0 , найти точку C , |
||||
|
|||||||||
|
ближайшую к началу координат. |
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
Вычислить y 3 функции y x28 ln x . |
|
|
|
|
|
|
|
|
6.Оценить с помощью формулы Тейлора абсолютную погрешность приближенной формулы: ctgx 1 2 x 2 x 2 , x .
4 4 4 2
7. |
Составить уравнения касательной и нормали к кривой |
x sin 2t |
в точке |
|||
|
|
|||||
|
t0 0 и вычислить yxx x0 . |
y et |
|
|
|
|
|
|
|
|
|
||
8. |
Вычислить производную 2-го порядка от неявной функции: 3 |
x 3 |
y 3 6 . |
|||
9. |
Вычислить предел с помощью формулы Тейлора: lim |
|
1 2x3 |
cos x4 |
||
|
|
|
|
. |
||
|
tgx |
x |
|
|||
|
x 0 |
|
|
|||
10.В какой точке касательная к кривой y ln x параллельна хорде соединяющей точки A 1;0 и B e;1 ?
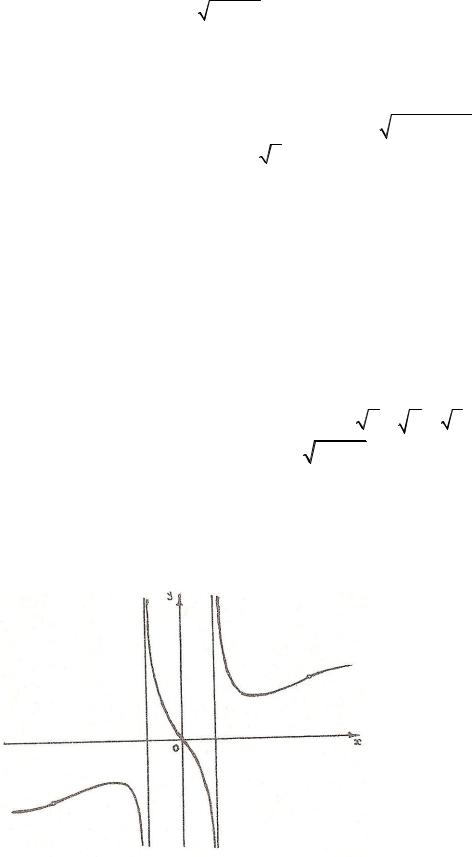
11.По графику функции построить график ее первой производной
32
|
|
|
|
|
|
|
|
|
|
Вариант 30 |
|
|
|
|
|
|
||||
1. |
Вычислить пределы с помощью правила Лопиталя: |
|
|
|
|
|
||||||||||||||
|
а) lim |
/ 2 |
arctgx |
|
; б) |
lim |
1 x |
2 |
|
1 / ln x |
. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
ln |
x |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x |
1 / 2 |
|
|
x 1 / |
|
1 |
|
x |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. |
Провести исследование и построить график функции |
y |
4x3 |
3x2 8x 2 |
. |
|||||||||||||||
|
2 |
3x2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3. |
Построить график функции в полярной системе координат r |
1 2cos2 . |
||||||||||||||||||
4. Найти радиус основания R и высоту H прямого кругового цилиндра, вписанного в сферу единичного радиуса и имеющего среди всех таких цилиндров наибольшую полную поверхность.
5. Вычислить y 3 функции y x20ex .
6. Оценить с помощью формулы Тейлора абсолютную погрешность
|
приближенной формулы: arcsin x x |
x3 |
, 0 x 0,5 . |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 t |
2 |
|
|
||
7. |
Составить уравнения касательной и нормали к кривой |
|
x |
|
в точке |
||||||
|
|
t t3 |
|||||||||
|
|
|
|
|
|
y |
|
|
|||
|
t0 2 и вычислить yxx x0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. |
Вычислить производную 2-го порядка от неявной функции: 3x 5 y2 . |
||||||||||
9. |
Вычислить предел с помощью формулы Тейлора: lim |
x |
1 sin x ln 1 x |
. |
|||||||
|
|
||||||||||
|
|
|
x 0 |
|
|
tgx sin x |
|||||
10. Удовлетворяют ли функции f x ex и |
|
|
|
|
|
|
|
|
|||
g x x2 / 1 |
x2 |
|
условиям теоремы |
||||||||
Коши на отрезке 3;3 ?
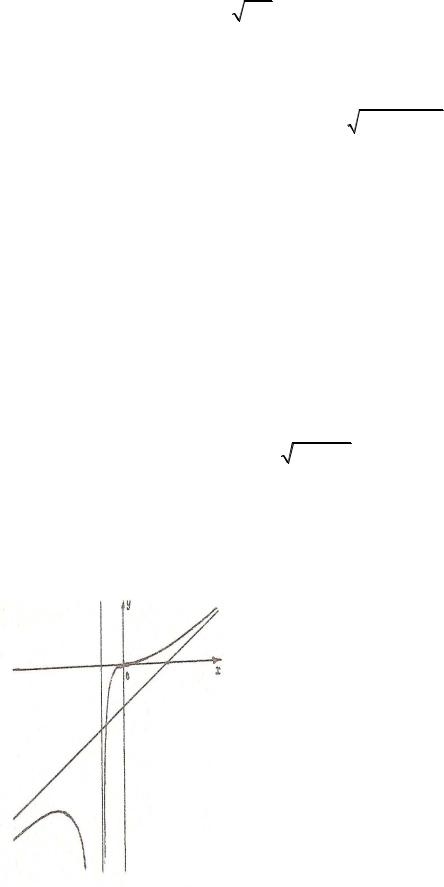
11. По графику функции построить график ее первой производной
33

2.Решение типового варианта по дифференциальному исчислению.
1.Вычислить пределы с помощью правила Лопиталя:
a)lim 1 x 1 ln x
|
1 |
|
|
lim |
x 1 ln x |
|
|
|
|
|
|||
x 1 |
x 1 ln x |
|||||
|
|
x 1 |
||||
0 |
|
1 |
|
1 |
|
0 |
|
|
|
|
|
|
x |
|
|
x 1 |
|
||||
lim |
lim |
|||||||||
0 |
|
|
|
0 |
|
|
|
|
||
|
x 1 |
ln x |
|
x 1 |
|
x 1 |
xln x x 1 |
|
|
|
|
|
x |
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 . |
|
0 |
|
|
|
|
|||
lim |
|
|
|
||||
|
x |
|
|
||||
|
x 1 |
ln x |
1 |
|
2 |
||
|
|
x |
|
||||
|
|
|
|
|
|
|
|
б) lim tgx 2 x
x 2 0
Это есть неопределённость вида 0. Обозначив выражение под знаком предела через y, рассмотрим
|
|
|
|
|
|
|
|
|
|
|
|
|
2x |
|
2 |
|
||||
lim ln y lim 2x ln tgx lim |
|
ln tgx |
|
|
|
|
|
|
||||||||||||
|
|
|
|
lim |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2x |
1 |
|
|
|
|
2tgx cos |
2 |
x |
|
|||||
x 2 0 |
x |
2 0 |
|
|
x 2 0 |
|
|
|
|
|
x 2 0 |
|
|
|||||||
|
2x |
2 |
|
2x |
2 |
0 |
|
|
|
|
2 2x 0 |
|
|
|
||||||
lim |
lim |
|
|
|
|
|
0. |
|||||||||||||
|
|
lim |
|
|||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2x |
|
|
|
|
|
|
|
|
|
|
|
||||||
x 0 |
2sin xcos x |
x 0 |
|
|
x |
0 |
2cos 2x |
|
1 |
|
|
|
||||||||
2 |
lim |
y 1. |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
Значит, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.Провести исследование и настроить график функции: y x 2arctgx Область определения: x R; функция является нечетной; она непрерывна
для всех x , поэтому её график вертикальных асимптот не имеет; наклонные и горизонтальные асимптоты:
k lim |
|
x 2arctgx |
1 2lim arctgx |
1, |
|
|
|
|
|
|
|
x |
|
|
|
|
|
||||
x |
|
x |
x |
|
|
|
|
|
|
|
b lim |
x 2arctgx x 2 lim arctgx 2 |
|
|
|
, |
|||||
|
2 |
|
||||||||
x |
|
|
|
x |
|
|
|
|
|
|
т.е. при x асимптотой является прямая |
y x , а при x |
|
||||||||||||||||||||
асимптотой является прямая y x . |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2 |
|
x |
2 |
|
1 |
|
x 1 |
x 1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Далее имеем: y |
|
1 |
1 x2 |
1 x2 |
|
1 x2 |
|
; знаки |
|
|
y |
: |
|
|
|
|||||||
|
|
|
|
|
|
|
1 |
1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
т.е. функция возрастает на интервалах , 1 и 1, и убывает на интервале 1,1 ; x 1 является точкой максимума, а x 1является точкой мини-
34
мума: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y 1 1 |
2 |
|
|
1 |
|
0,57, |
|
|
y 1 1 |
2 |
|
1 |
0,57, |
||||||||||||
|
|
4 |
|
2 |
|
|
|
|
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|||||
|
2x 1 x |
2 |
|
x |
2 |
1 2x |
|
|
|
4x |
|
|
|
|
|
|
|
|
|
|
|||||
y |
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||
|
|
1 x |
|
|
|
|
|
|
|
1 x |
|
|
|
|
|
|
|
|
|
|
|||||
знаки y : |
|
|
|
|
|
|
|
|
|
|
|
|
т.е. график функции будет выпуклым на |
||||||||||||
0
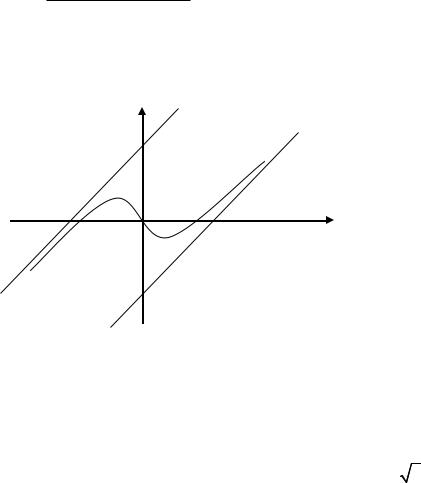
интервале ,0 , и вогнутым на интервале 0;1 ; точка 0;0 будет точкой перегиба графика; y 0 1. График функции будет иметь вид:
11
3. Построить график функции в полярной системе координат: r sin 3
График строится “по точкам” с учетом того, что r |
возрастает при |
|
|
|
||||||||||||||
0 |
|
, то есть при 0 |
3 , и убывает при |
|
|
|
, то есть при |
|
|
|||||||||
|
3 |
2 |
|
2 |
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
1 |
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
3 ; r 0 0, r |
sin |
|
|
|
, r sin |
|
|
|
, r |
|
sin |
|
1, |
|||
2 |
6 |
2 |
3 |
2 |
2 |
|||||||||||||
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|||||||
r 3 |
sin 0 и так далее. В итоге, график будет иметь вид: |
|
|
|
|
|||||||||||||
35
4.Найти радиус основания и высоту конуса наименьшего объема, описанного около сферы единичного радиуса. V 13 Aa2 Ba 13 R2 H .
Из подобия треугольников AaB è EOB
|
|
|
B |
|
|
EO |
|
|
EB |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
; т.к. AE Aa R, то отсюда |
||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
Aa |
Ba |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
E |
|
|
F |
|
|
|
1 |
|
|
BO2 EO2 |
|
|
H 1 2 1 |
. |
||||||||||||
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|||||||||||||
|
|
|
О |
|
|
|
R |
|
|
|
|
|
|
|
H |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Теперь R |
|
|
|
|
|
|
|
|
||||||||
A |
|
|
|
|
C |
H 2 2H |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
и V 1 |
|
|
H 3 |
|
1 |
|
H 2 |
|
, где H 2, . |
||||||||||
|
|
|
|
|
|
|
H |
2 2H |
H |
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|
|||||||||
Найдем, при каком H эта функция будет наименьшей: |
|
|
|
|||||||||||||||||||||||
1 2H H 2 H 2 |
|
H H 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
V 3 |
|
|
|
|
|
|
|
0. т.к. H 0, |
то отсюда H 4. |
|||||||||||||||||
|
H 2 2 |
H 2 2 |
||||||||||||||||||||||||
Знаки V : |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Значит, V убывает на 2,4 и возрастает на 4, |
и функция будет |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
наименьшей при H 4. |
|
Тогда R |
|
|
|
|
4 |
|
|
|
|
|
4 |
|
|
|
2. Таким |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
16 8 |
2 2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
образом, |
|
H 4, R |
|
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
5. Вычислить y |
7 |
|
функции y |
|
x2 |
1 |
|
. Разделим числитель на знаменатель |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x2 |
2x |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
и разложим оставшуюся правильную дробь на простые: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
y |
x2 2x 2x 1 |
1 |
|
|
2x 1 |
|
; |
|
|
2x 1 |
|
|
|
|
A |
|
|
|
B |
|
; 2x 1 A x 2 Bx; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x x 2 |
|
|
x x 2 |
x |
|
|
x 2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x2 2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
при x 0 отсюда |
2A 1, |
A 1 |
; при x 2 |
отсюда 2b 3, |
B |
3 . |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
Таким образом, y 1 |
|
1 |
|
|
3 |
|
|
|
|
|
. Теперь легко найти искомую произ- |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2x |
2 |
x 2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
водную: y 7 |
|
1 2 ... 7 3 1 2 ... |
7 7! 1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x |
|
|
8 |
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
x |
2 |
8 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Теперь вычислим y 7 функции |
|
y |
x2 |
|
|
|
e x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
Используя формулу Лейбница при u e x , |
v x2 1, |
имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
y |
|
7 |
u |
7 |
|
v |
|
|
7u |
6 |
|
|
|
7 6 |
v |
|
|
(все остальные члены будут равны 0); |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
y 7 e x |
|
x2 |
|
|
|
7e x 2x 21e x |
|
2 e x |
|
x |
2 1 14x 42 |
|
e x |
|
x2 14x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
41 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
6. Используя формулу Тейлора 2-ого порядка, вычислить приближенно |
|
5 |
и |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
доказать, что при этим погрешность r |
допускает оценку |
|
|
|
r |
|
|
|
1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
10 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5 |
|
4 1 2 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||||
Далее используем формулу |
|
f |
x 1 x |
1 x |
x2 r, |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 , |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
в которой |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
1 |
|
3 |
|
||||||||||||||||||||
è |
|
r f |
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
c |
|
|
|
x3 |
|
|
|
2 |
2 |
2 |
1 c |
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
3! |
|
|
|
|
|
|
|
|
3! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
3 24 |
26 |
|
|
|
1 c 5 |
|
210 |
|
1 c 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
37

C между O и |
1 |
. Отбрасывая остаточный член r, имеем приближенно |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1 |
|
1 |
|
|
2 |
|
2 |
|
|
1 |
|
|
|
|
1 |
|
1 |
|
|
15 |
|
|||
|
2 |
1 |
|
|
|
|
|
|
|
|
2 |
|
|
2 |
2,234375 |
|||||||||||||
5 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||
2 |
4 |
|
|
2! |
|
4 |
2 |
8 |
128 |
64 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Погрешность этих вычислений допускает оценку |
|
r |
|
|
|
|
|
1 |
|
|
|
1 |
, т.к. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 c 5 |
210 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
210 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
наибольшее значение этой дроби будет при наименьшем её знаменателе, |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
т.е. при |
|
c 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x a t sin t |
|
|
|||||||
7. Составить уравнения касательной и нормали к кривой |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
a 1 cost |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в точке t0 |
и вычислить yxx |
x0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
yt |
|
|
|
asin t |
|
|
2sin |
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
yx |
|
|
|
|
2 |
2 |
|
ctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
x |
a 1 cost |
|
2sin |
2 |
t |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
t |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
yx t0 ctg |
|
1; y t0 a |
1 0 a; |
|
|
|
|
x t0 x0 a |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
4 |
|
|
|
|
|
2 |
1 . |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Уравнение касательной имеет вид y a 1 x a |
|
|
1 |
|
; |
y x a |
|
2 |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Уравнение нормали имеет вид |
|
|
y a |
1 |
|
|
|
|
|
|
|
|
|
|
|
y x |
a |
; |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
1 |
x a |
2 |
|
|
1 |
; |
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
yx t |
|
|
|
|
|
2sin2 |
t |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Далее имеет: |
yxx |
|
|
|
|
|
2 |
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
x |
|
a 2sin |
2 |
|
t |
4asin |
4 |
|
t |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
yxx x0 |
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
16 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
4asin |
4 |
4a |
|
|
|
|
2 |
|
4 |
4a 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
8.Вычислить производную 2-го порядка от неявной функции: y 1 xe y , т.е. y 1 xe y 0; дифференцируем это равенство по x : yx e y xe y yx 0,
38
откуда |
yx 1 xe |
y |
e |
y |
|
|
yx |
|
e y |
|
|
e y |
|
|
||||||||||
|
|
|
è |
|
y . |
|
|
|||||||||||||||||
|
|
|
|
1 xe y |
|
|
||||||||||||||||||
Дифференцируем это равенство по x еще раз: |
|
|
||||||||||||||||||||||
|
|
e |
y |
|
e |
y |
y |
|
|
|
e y |
|
y 1 |
|
|
e y |
|
y 1 |
|
y |
||||
yxx |
|
|
y y |
|
|
|
|
|
|
|
|
y |
|
|
|
e |
|
|||||||
|
|
|
y |
|
|
|
|
|
|
|
|
y |
|
|
|
y |
y |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
e 2 y y 1 |
. |
|
y2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2x e |
2 x |
4 |
|
|
|
|
|
|
||||||||
9. |
Вычислить предел с помощью формулы Тейлора: lim |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
sin |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
x |
4 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это есть неопределённость вида |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Обозначим x |
|
t, |
x t ; тогда наш предел будет равен |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
e |
2t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
sin 2t |
|
|
|
lim cos 2t |
e |
2t2 |
t |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
lim |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
, что в силу 1-ого |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
sin4 t |
|
|
|
|
|
|
|
|
|
|
|
|
sin4 t |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
t 0 |
|
|
|
|
|
|
|
t 0 |
|
t4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
замечательного |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
предела lim |
sin |
1, приводит к |
lim |
|
cos 2t e 2t2 |
. Далее используем готовые |
|||||||||||||||||||||||||||||||||||||||||||||||
|
x |
|
|
|
t4 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x 0 |
|
|
|
|
|
|
|
|
t2 |
t4 |
t |
0 |
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
4 |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
2 |
; подставляя в |
|||||||||||||||||||
|
разложения |
|
cost 1 |
2! |
4! 0 |
|
|
|
и |
|
e |
|
|
1 t 2! 0 t |
|
|||||||||||||||||||||||||||||||||||||||
|
них вместо t |
2t |
|
è |
|
|
2t2 |
соответственно, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
4t2 |
|
16t4 |
|
4 |
|
|
|
|
|
|
|
2 |
|
2 |
|
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
cos 2t 1 |
|
2 |
|
|
0 t |
|
1 |
|
2t |
|
|
3 t |
|
|
0 t |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
4 3 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
e 2t2 |
1 2t2 |
4t4 |
|
0 t4 1 2t2 2t4 0 t4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
Теперь исходный предел будет равен |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
1 2t2 |
2 t |
4 1 2t2 2t |
4 0 |
|
t4 |
|
|
|
|
|
|
2 |
|
|
0 t4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
t4 |
|
|
|
4 |
|
|
|
|
0 |
t |
4 |
|
|
||||||||||||||||||||||||||||||||
|
lim |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
lim |
|
; |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
t4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t4 |
|
|
|
3 |
|
t4 |
|
|
|
||||||||||||||||
|
t 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t 0 |
|
|
|
|
|
||||||||||
|
поскольку последний предел, согласно определению бесконечно малой |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
более высокого порядка, равен 0, |
то получаем ответ: 4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
, e |
2 |
|
|
|
|
|
|
|
|
|
||||
10. |
Написать формулу Лагранжа для функции y ln 2x, |
x |
|
|
и найти |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
соответствующую точку C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
b f a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
Формула Лагранжа имеет вид f |
f |
|
c , |
c a,b ; |
|
для нашей |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
b a |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
39
функции будем иметь |
ln e2 |
ln e |
|
2 |
|
x c |
, т.е. |
2 1 |
1 |
и c e2 e. |
|
||||||||||
e2 e |
2x |
|
||||||||
|
|
|
e2 e c |
|
||||||
11.По графику функции построить график её первой производной. Под графиком функции будем строить график её производной, учитывая что:
-на интервалах возрастания функции , 1 и 1, её производная
положительна, а на интервале убывания 1,1 это производная отрицательна;
-точки 1 и 1 являются точками экстремума функции, значит производная |
|
функции в этих точках равна 0 или не существует: y 1 0, |
y 1 не |
существуют, т.к. в этой график функции имеет вертикальную касательную, а в силу того, что производная – это угловой коэффициент касательной,
y 1 lim kкасат . ;
x 1
-аналогично, т.к. график функции имеет вертикальную касательную и в точке 2 , то в этой точке производная также имеет бесконечный разрыв;
-т.к. при x график функции имеет асимптоту (предположительно
y x ), то график её производной будет иметь горизонтальную асимптоту y x , т.е. y 1.
40
