
Вариант 18
1. Вычислить пределы с помощью правила Лопиталя: |
||||||||
|
2 |
|
|
|
1 |
ln 1 x |
|
|
а) lim xln |
|
arctgx |
; б) |
lim |
|
|
. |
|
|
||||||||
x |
|
|
|
x 0 |
x |
|
|
|
2. Провести исследование и построить график функции: y xx .
3. Построить график функции в полярной системе координат |
r 1 cos |
. |
|
|
3 |
4.Найти сторону основания a и боковое ребро b правильной четырехугольной призмы, вписанной в сферу единичного радиуса и имеющей среди всех таких призм наибольшую полную поверхность.
5. |
Вычислить y 18 функции y xln |
3 |
x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3 |
x |
|
|
|
|
|
||
6. |
Вычислить с помощью формулы Тейлора: sin10 с точностью до 10 6 . |
|
|||||||
|
|
|
|
|
|
t |
2 |
|
|
7. |
Составить уравнения касательной и нормали к кривой |
x ln 1 |
|
в точке |
|||||
|
|
|
|
||||||
|
|
|
|
|
y t arctgt |
|
|||
|
|
|
|
|
|
|
|
|
|
|
t0 1 и вычислить yxx x0 . |
|
|
|
x y |
|
|
||
8. |
Вычислить производную 2-го порядка от неявной функции: |
x . |
|||||||
x y |
|||||||||
|
|
|
|
|
|
|
|||
|
|
|
ln x x 1 ex 1 |
||||||
9. |
Вычислить предел с помощью формулы Тейлора: |
lim |
|
|
|
|
|
. |
|
|
2 x 1 |
3 |
|
||||||
|
|
x 1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
10. Доказать, что функция f x , где f x x 4 2 |
x 2 |
2 , имеет на |
|||||||
|
промежутке 2;4 два корня. |
|
|
|
|
|
|
|
|
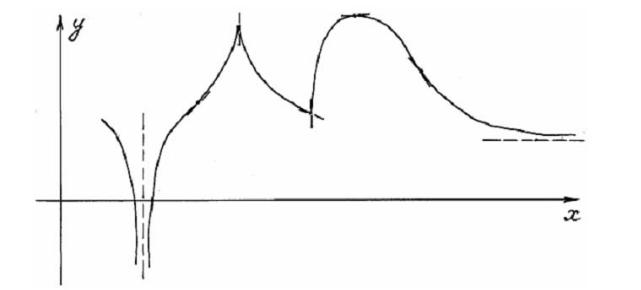
11. По графику функции построить график ее первой производной
21

Вариант 19
1. |
Вычислить пределы с помощью правила Лопиталя: |
|
|
|
|
||||||||
|
а) lim x |
|
2arcsin |
|
x / |
x2 1 |
|
; б) lim sin 2x 1/lnsin x . |
|
|
|
|
|
|
x |
|
|
|
x 0 |
|
|
|
|
||||
2. |
Провести исследование и построить график функции: y arcsin |
|
4x |
. |
|||||||||
4 x2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||
3. |
Построить график функции в полярной системе координат r |
|
2 |
; 0;2 |
|||||||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
4.Найти сторону основания a и боковое ребро b правильной шестиугольной призмы, вписанной в сферу единичного радиуса и имеющей среди всех таких призм наибольший объем.
5. |
Вычислить y 19 функции y xln x2 3x 2 . |
|
|
|
|
|
|
|
|||
6. |
Вычислить с помощью формулы Тейлора: cos50 с точностью до 10 5 . |
|
|
||||||||
7. |
Составить уравнения касательной и нормали к кривой |
x cos 2t |
|
|
в точке |
||||||
|
2 / cos2 t |
||||||||||
|
|
|
|
|
y |
|
|
||||
|
t0 |
и вычислить yxx x0 . |
|
|
|
|
|
|
|
||
|
|
|
4 |
|
|
|
|
|
|
|
|
8. |
Вычислить производную 2-го порядка от неявной функции: y2 2 2 px . |
|
|||||||||
9. |
Вычислить предел с помощью формулы Тейлора: |
lim |
2xex 2 |
x3 6x2 10x |
. |
||||||
|
x |
2 |
2 |
|
|||||||
|
|
|
|
|
x 2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
10. Написать формулу Коши для функций f x x2 |
и g x |
x , и найти c на |
|||||||||
|
|
|
|
. |
|
|
|
|
|
|
|
|
1;4 |
|
|
|
|
|
|
|
|
||
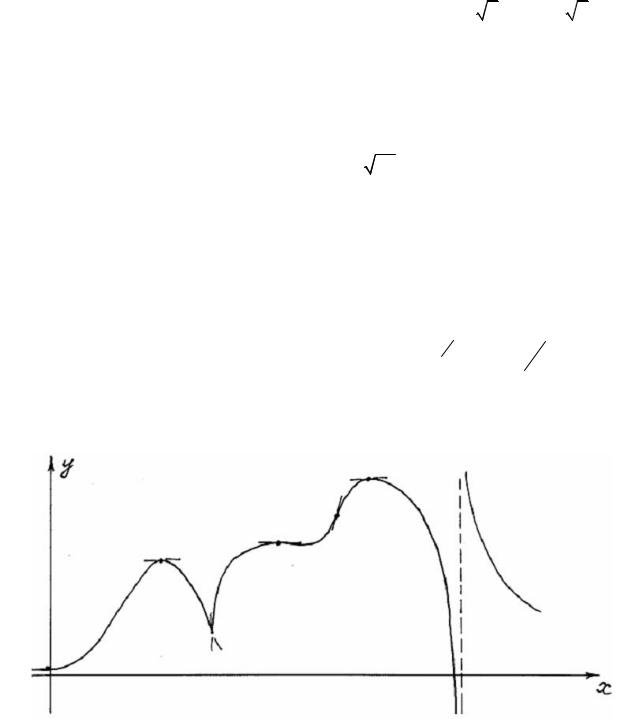
11. По графику функции построить график ее первой производной
22
|
|
|
|
|
|
Вариант 20 |
|
|
1. |
Вычислить пределы с помощью правила Лопиталя: |
|
|
|||||
|
|
1 |
|
1 |
|
lim 1 x ln x . |
|
|
|
а) lim |
; б) |
|
|
||||
|
|
2 |
|
|
||||
|
x 0 xarctgx |
|
x |
|
x 0 |
x ln 1 3 |
x . |
|
2. |
Провести исследование и построить график функции y 3 |
|||||||
3.Построить график функции в полярной системе координат r 0,5 ; 0;2
4.На окружности x2 y2 4x 6 y 12 0 найти такую точку C , чтобы сумма квадратов расстояний от неё до двух точек A 6;1 и B 5;5 была наименьшей.
5. |
Вычислить y 20 функции |
y x3 cos x . |
|
|
|
|
|
|
6. |
Вычислить с помощью формулы Тейлора: 3 30 с точностью до 10 4 . |
|
|
|
||||
|
|
|
|
2 |
/ t |
2 |
1 |
|
7. |
Составить уравнения касательной и нормали к кривой x 1 |
t |
|
|
в |
|||
|
|
y t / t2 |
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
точке t0 2 и вычислить yxx x0 .
8.Вычислить производную 2-го порядка от неявной функции: (x y)2 6(x y) .
9.Вычислить предел с помощью формулы Тейлора: lim 2 cos2 x 2sin x .
2 x 2 4
10.Написать формулу Лагранжа для функции f x x3 и найти c .
11.По графику функции построить график ее первой производной
23

Вариант 21
1. Вычислить пределы с помощью правила Лопиталя:
а) lim |
2x 2 |
|
1 x 1 x 1x |
|||
|
2 |
|
; б) lim |
. |
||
|
2 |
cos |
x |
|
e |
|
x |
|
|||||
|
|
|
|
x 0 |
|
|
2.Провести исследование и построить график функции y xarctgx .
3.Построить график функции в полярной системе координат r 10cos 3.
4.Найти сторону основания a и боковое ребро b правильной треугольной пирамиды, вписанной в сферу единичного радиуса и имеющей среди всех таких пирамид наибольшую боковую поверхность.
5. Вычислить y 21 |
функции y 2xcos2 x / 3 . |
6.Cчитая, что ln10 2,30258, вычислить lg11с помощью формулы Тейлора с точностью до 10 4 .
|
|
|
|
t |
|
|
|
7. |
Составить уравнения касательной и нормали к кривой |
x e |
в точке |
||||
|
|||||||
|
t0 0 и вычислить yxx x0 . |
y arcsin t |
|
|
|||
|
|
|
|
|
|||
8. |
Вычислить производную 2-го порядка от неявной функции: x2 y2 |
2 . |
|||||
9. |
Вычислить предел с помощью формулы Тейлора: lim |
ln 1 x2 x2e x2 |
. |
||||
|
|||||||
|
x 0 |
|
x3 |
|
|
||
10. Будет ли выполняться теорема Ролля для функции y 3 8x x2 на отрезке
0;8 .
11. По графику функции построить график ее первой производной
24

Вариант 22
1. |
Вычислить пределы с помощью правила Лопиталя: |
|
|||
|
|
1 |
|
|
|
|
а) lim x3 ln2 x ; б) |
lim x |
ln shx |
. |
|
|
x 0 |
x 0 |
x2 1 . |
||
2. |
Провести исследование и построить график функции y ln x |
||||
3. |
Построить график функции в полярной системе координат r 2 |
1 cos . |
|||
4.Найти сторону основания a и боковое ребро b правильной треугольной пирамиды, вписанной в сферу единичного радиуса и имеющей среди всех таких пирамид наибольший объем.
5. Вычислить y 22 функции y x2 |
x cos2 x . |
|
|
|
|
|
||||
6. |
Оценить с помощью формулы Тейлора абсолютную погрешность |
|
|
|||||||
|
n |
|
k |
|
|
|
|
|
|
|
|
приближенной формулы: ex |
x |
|
,0 x 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
k 0 |
k! |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
x cost |
|
|
|
7. |
Составить уравнения касательной и нормали к кривой |
|
|
|
|
|||||
|
t / 2 |
|
||||||||
|
|
|
|
|
|
|
y sin4 |
|||
|
t0 и вычислить yxx x0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3 |
|
|
|
|
|
|
|
|
|
8. |
Вычислить производную 2-го порядка от неявной функции: y 0.5sin |
|||||||||
9. |
Вычислить предел с помощью формулы Тейлора: lim |
ex2 1 xsin x |
. |
|
||||||
|
x4 |
|
|
|||||||
|
|
|
|
|
x 0 |
|
|
|
|
|
в точке
y x .
10.В какой точке касательная к параболе y x2 параллельна хорде, соединяющей точки A 1;1 и B 3;9 ?
11.По графику функции построить график ее первой производной
25
Вариант 23
1. Вычислить пределы с помощью правила Лопиталя:
|
|
1 |
|
arctgx |
|
|
3x |
2 |
3 |
x |
|
1 x |
|
|||
а) lim |
|
|
|
4 |
|
; б) |
lim |
|
|
|
. |
|||||
|
3 |
x |
|
|
|
|||||||||||
x 0 |
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
||
1
2.Провести исследование и построить график функции y x 2 ex .
3.Построить график функции в полярной системе координат r 0 r 3ctg .
4.На правой ветви гиперболы y 12x , x 0 , найти точку C , ближайшую к прямой l : 3x 4 y 16 0 .
5. |
Вычислить y 23 функции y |
|
x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
5x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
6. |
Оценить с помощью формулы Тейлора абсолютную погрешность |
|
|
|||||||||||||||||
|
приближенной формулы: sin x x |
x3 |
|
x5 |
, |
|
x |
|
1. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
3! |
|
5! |
|
|
|
|
x arctgt |
в точке |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
7. |
Составить уравнения касательной и нормали к кривой |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
t0 1 и вычислить yxx x0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y t2 |
/ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8. |
Вычислить производную 2-го порядка от неявной функции: ex ey y x . |
|||||||||||||||||||
9. |
Вычислить предел с помощью формулы Тейлора: |
|
ln 1 x |
xe x |
||||||||||||||||
lim |
|
|
|
|
. |
|||||||||||||||
|
x2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
||
10.Проверить, что между корнями функции f (x) x2 4x 3 находится корень
еепроизводной. Пояснить графически.
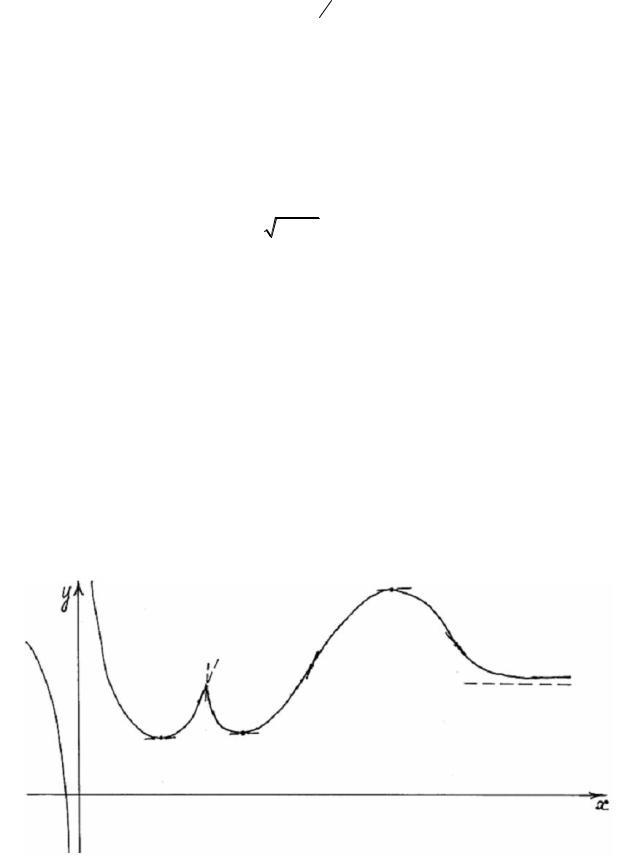
11.По графику функции построить график ее первой производной
26
Вариант 24
1. Вычислить пределы с помощью правила Лопиталя: |
||||
а) lim |
arctg x 1 |
; б) |
lim |
2x cos x . |
|
||||
x 1 |
x2 x 2 |
|
|
|
x 2 |
||||
1
2.Провести исследование и построить график функции y xe x2 .
3.Построить график функции в полярной системе координат r 0 r 3cos 1 3 .
4.Найти сторону основания a и боковое ребро b правильной шестиугольной призмы, вписанной в сферу единичного радиуса и имеющей среди всех таких призм наибольшую полную поверхность.
5. |
Вычислить y |
24 |
функции |
y |
|
x2 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2x |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6. |
Оценить с помощью формулы Тейлора абсолютную погрешность |
|
|
|||||||||||||||||
|
приближенной формулы: |
cos x 1 |
x2 |
|
x4 |
|
x6 |
, |
|
x |
|
0,5 . |
|
|
||||||
|
|
|
|
|
||||||||||||||||
|
2! |
4! |
6! |
|
|
|
|
|||||||||||||
7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
x tgt |
в точке |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Составить уравнения касательной и нормали к кривой |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 1 / sin 2t |
|
|
|
t0 и вычислить yxx x0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. |
Вычислить производную 2-го порядка от неявной функции: y ln y x . |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ex ln 1 x 2 |
e x |
|
9. |
Вычислить предел с помощью формулы Тейлора: lim |
|
|
. |
||||||||||||||||
x2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
на 1;2 . |
||||
10. Написать формулу Лагранжа для функции f x x3 |
5 и найти c |
|||||||||||||||||||
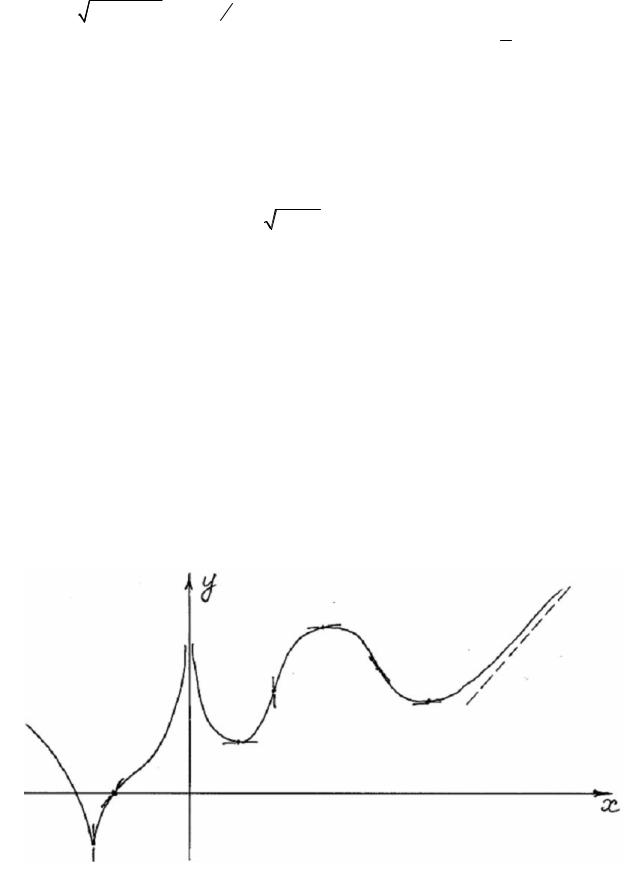
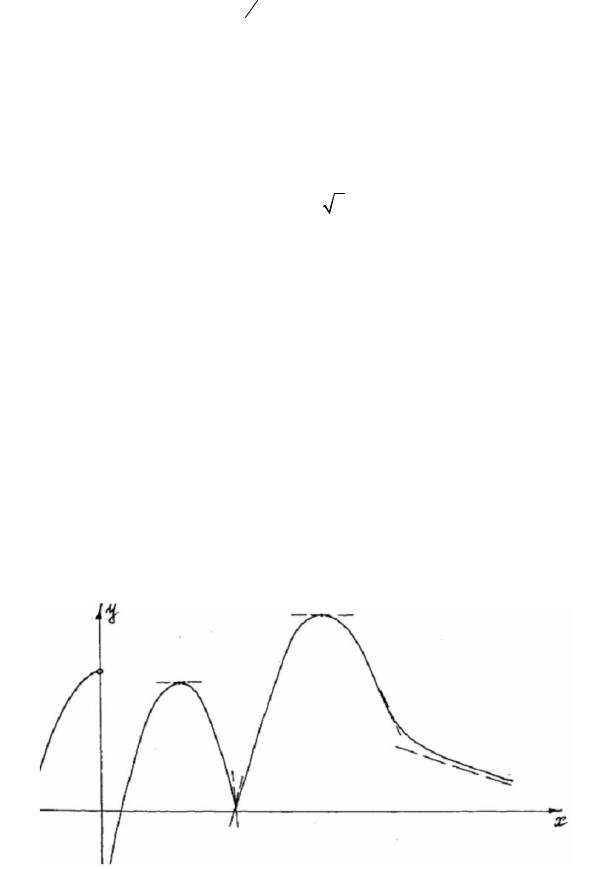
11. По графику функции построить график ее первой производной
27
|
|
|
|
|
|
|
Вариант 25 |
|
|
|
|
|
1. |
Вычислить пределы с помощью правила Лопиталя: |
|
|
|
|
|
||||||
|
а) lim arcsin x arctgx |
; б) |
lim |
tgx cos x . |
|
|
|
|
|
|||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
x 0 |
ln 1 x |
|
|
|
x 2 |
|
|
|
|
|
|
2. |
Провести исследование и построить график функции y ln x |
2 |
1 |
|
1 |
. |
||||||
|
x2 |
1 |
||||||||||
3.Построить график функции в полярной системе координат r 0 r 3sin 1 3 .
4.Найти радиус основания R и высоту H прямого кругового цилиндра, вписанного в сферу единичного радиуса и имеющего среди всех таких цилиндров наибольший объем.
|
Вычислить y |
3 |
|
|
x/2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||
5. |
|
функции |
y e |
|
cos |
|
|
|
|
|
|
x . |
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6. |
Оценить с помощью формулы Тейлора абсолютную погрешность |
|
|
|
|||||||||||||||||
|
приближенной формулы: |
tgx x |
x3 |
, |
|
x |
|
0,1. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
3 |
|
|
|
|
x cost sin t |
в точке |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
7. |
Составить уравнения касательной и нормали к кривой |
||||||||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y sin 2t |
|
|
|
|
|
t0 и вычислить yxx x0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. |
Вычислить производную 2-го порядка от неявной функции: y cos(x y) . |
|
|||||||||||||||||||
9. |
Вычислить предел с помощью формулы Тейлора: lim |
ln 1 2x 2x2 |
sin 2x |
. |
|||||||||||||||||
|
x3 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
||
10.На кривой y x3 найти точку, в которой касательная параллельна хорде, соединяющей точки A 1; 1 и B 2,8 .
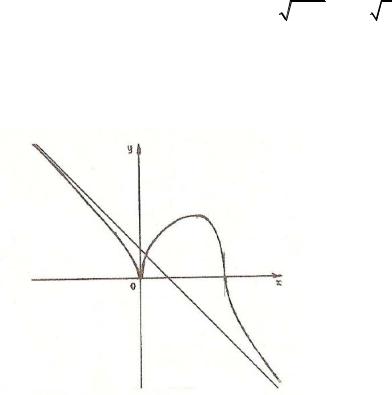
11.По графику функции построить график ее первой производной
28
|
|
|
|
|
|
|
|
|
Вариант 26 |
|
|
|
1. |
Вычислить пределы с помощью правила Лопиталя: |
|
|
|
||||||||
|
|
|
|
1 |
|
|
|
|
|
|
||
|
а) lim |
1 |
|
|
|
|
; б) |
lim xx . |
|
|
|
|
|
|
e |
x |
1 |
|
|
|
|||||
|
x 0 tgx |
|
|
x 0 |
|
|
|
|||||
2. |
Провести исследование и построить график функции |
y |
ln x |
. |
||||||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
3. Построить график функции в полярной системе координат r 0 r sin .
4.На отрезке прямой между точками A 2;1 и B 4;5 найти такую точку C ,
чтобы сумма квадратов расстояний от неё до двух прямых: l1 : 4x y 8 0 , и l2 : x y 10 0 , была наименьшей.
5. |
Вычислить y 3 функции y e2 x sin2 x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
Оценить с помощью формулы Тейлора абсолютную погрешность |
|
|
|||||||||||||
|
приближенной формулы: ln 1 x x |
x2 |
|
x3 |
|
x4 |
, |
|
x |
|
0,1. |
|
|
|
||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||
|
2 |
3 |
4 |
|
|
|
|
|
|
|
3 |
|
|
|||
|
|
|
|
|
|
|
|
|
||||||||
7. |
Составить уравнения касательной и нормали к кривой |
|
x t |
в точке |
||||||||||||
|
|
|||||||||||||||
|
t0 и вычислить yxx x0 . |
|
|
|
|
|
|
|
|
|
y sin t |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8. |
Вычислить производную 2-го порядка от неявной функции: x2 3xy y2 1. |
|||||||||||||||
9. |
Вычислить предел с помощью формулы Тейлора: lim |
|
|
ex |
1 x |
|
. |
|||||||||
|
|
1 x cos |
x |
|||||||||||||
|
|
|
|
|
|
x 0 |
|
|
||||||||
10. Написать формулу Коши для функций |
f x x2 2x 3 |
|
и |
|
|
|||||||||||
|
g x x3 7x2 20x 5 , и найти c на 1;4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
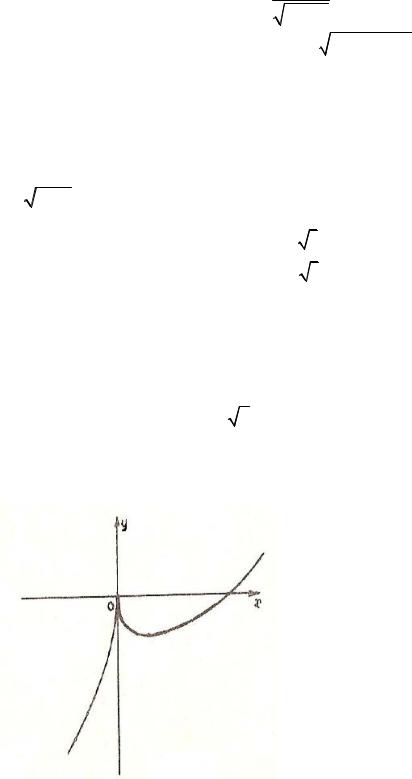
11. По графику функции построить график ее первой производной |
|
|
||||||||||||||
29
Вариант 27
1. Вычислить пределы с помощью правила Лопиталя:
|
|
2 |
|
|
1 |
; б) lim x |
ln 3 / 1 x |
. |
||
а) lim |
|
|
|
|
|
|
||||
|
2 |
x |
|
|
||||||
x 0 |
sin |
|
|
1 cos x |
x 1 |
|
|
|||
2. Провести исследование и построить график функции y
x .
3 x2 1
3. Построить график функции в полярной системе координат r |
1 2sin 2 . |
4.Найти основание a и боковую сторону b равнобедренного треугольника, вписанного в окружность единичного радиуса и имеющего среди всех таких треугольников наибольший периметр.
5. |
Вычислить y 4 функции |
y x2 sin2 x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
Оценить с помощью формулы Тейлора абсолютную погрешность |
|
|
||||||||||||||||
|
приближенной формулы: |
1 x 1 |
x |
|
x2 |
|
|
x3 |
,0 x 0,2 . |
|
|
|
|
|
|
||||
|
2 |
8 |
16 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
7. |
Составить уравнения касательной и нормали к кривой |
x |
|
в точке |
t0 |
26 |
|||||||||||||
|
|
t |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
3 |
|
|
|
|
|
|
|
и вычислить yxx x0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. |
Вычислить производную 2-го порядка от неявной функции: ey 4x 7 y . |
|
|
||||||||||||||||
9. |
Вычислить предел с помощью формулы Тейлора: lim |
xcos x arctgx |
. |
|
|
||||||||||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
ln 1 x |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
10. Написать формулу Лагранжа для функции f x |
3x3 3x и найти c на |
|
|||||||||||||||||
|
0;1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11. По графику функции построить график ее первой производной
30
