Черноусова / ЗАДАНИя ДИСКР МАТЕМ ЧАСТЬ 1

Вариант 21

1. Проверить, верно ли тождество: x ( y z) (x y) (x z)

(если тождество не верно, то все задания делать по левой части)

а) используя определения операций над множествами

б) с помощью алгебры логики.

Изобразить результат на кругах Эйлера. Соответствующую булеву функцию привести к СДНФ, СКНФ, построить многочлен Жегалкина.

2. Для заданной булевой функции f x1, x2 , x3 , x4 V 2,3,4,6,7,12,15 :

а) составить таблицу истинности;

б) составить СДНФ и минимизировать методом Квайна;

в) представить результат в скобочной форме;

г) построить логическую схему, используя полученную минимальную функцию и сделать проверку по таблице истинности.

x y z 1

4.Составить систему уравнений с булевыми переменными и найти ее решение.

1)Неверно, что работает «в» или работает агрегат «с».

2)Если работает агрегат «в», то работает агрегат «с».

3)Агрегат «а» работает тогда и только тогда, когда работает агрегат «в».

4)Агрегат «в» работает тогда и только тогда, когда работает агрегат «d».

5.Решить задачу:

Сколькими способами можно раздать 6 карт четырем игрокам, если в колоде 36 карт?

Вариант 22

1. Проверить, верно ли тождество: x ( y z) (x y) (x z)

(если тождество не верно, то все задания делать по левой части)

а) используя определения операций над множествами

б) с помощью алгебры логики.

Изобразить результат на кругах Эйлера. Соответствующую булеву функцию привести к СДНФ, СКНФ, построить многочлен Жегалкина.

2. Для заданной булевой функции f x1, x2 , x3 , x4 V 0,1,5,6,8,9,14 :

а) составить таблицу истинности;

б) составить СДНФ и минимизировать методом Квайна;

в) представить результат в скобочной форме;

г) построить логическую схему, используя полученную минимальную функцию и сделать проверку по таблице истинности.

4. Составить систему уравнений с булевыми переменными и найти ее решение.

1) Неверно, что работает агрегат «в» или работает агрегат «с».

2) Агрегат «d» работает тогда и только тогда, когда работает агрегат «с».

3) Если работает агрегат «в», то работает агрегат «с».

4) Либо работает агрегат «а», либо работает агрегат «в».

5. Решить задачу:

Для участия в ежегодной эстафете выбраны 3 девушки и 7 юношей. Сколькими способами можно расставить их на этапах, чтобы начинали и заканчивали эстафету юноши?

Вариант 23

1. Проверить, верно ли тождество:x ( y z) (x y) (x z)

(если тождество не верно, то все задания делать по левой части)

а) используя определения операций над множествами

б) с помощью алгебры логики.

Изобразить результат на кругах Эйлера. Соответствующую булеву функцию привести к СДНФ, СКНФ, построить многочлен Жегалкина.

2. Для заданной булевой функции f x1, x2 , x3 , x4 V 4,5,6,9,11,12,14 :

а) составить таблицу истинности;

б) составить СДНФ и минимизировать методом Квайна;

в) представить результат в скобочной форме;

г) построить логическую схему, используя полученную минимальную функцию и сделать проверку по таблице истинности.

x y z 1

3. Решить систему логических уравнений: x y z 1

x y z 1

4. Составить систему уравнений с булевыми переменными и найти ее решение.

1)Если работает агрегат «в», то работает агрегат «с».

2)Работает агрегат «а» или работает агрегат «в».

3)Если работает агрегат «с», то работают агрегаты «а» и «d».

4)Агрегат «в» работает тогда и только тогда, когда работает агрегат «с».

5) Агрегат «d» работает тогда и только тогда, когда работает агрегат «с». 5. Решить задачу:

Сколькими способами можно рассадить 6 гостей на 8 стульях?

Вариант 24

1. Проверить, верно ли тождество: x ( y z) (x y) (x z)

(если тождество не верно, то все задания делать по левой части)

а) используя определения операций над множествами

б) с помощью алгебры логики.

Изобразить результат на кругах Эйлера. Соответствующую булеву функцию привести к СДНФ, СКНФ, построить многочлен Жегалкина.

2. Для заданной булевой функции f x1, x2 , x3 , x4 V 0,2,3,4,10,11,15 :

а) составить таблицу истинности;

б) составить СДНФ и минимизировать методом Квайна;

в) представить результат в скобочной форме;

г) построить логическую схему, используя полученную минимальную функцию и сделать проверку по таблице истинности.

4.Составить систему уравнений с булевыми переменными и найти ее решение.

1)Либо работает агрегат «с», либо работает агрегат «d».

2)Если работает агрегат «с», то работает агрегат «d».

3)Если работает агрегат «а», то работает агрегат «в».

4)Если работает агрегат «в», то работает агрегат «с».

5)Агрегат «в» работает тогда и только тогда, когда работает агрегат «с».

5.Решить задачу:

Для шести менеджеров проводится психологический тренинг в течение двух дней. Каждый день их объединяют в группы по три человека. Сколькими способами можно распределить менеджеров так, чтобы состав группы не повторялся?

Вариант 25

1. Проверить, верно ли тождество: x ( y z) (x y) (x z)

(если тождество не верно, то все задания делать по левой части)

а) используя определения операций над множествами

б) с помощью алгебры логики.

Изобразить результат на кругах Эйлера. Соответствующую булеву функцию привести к СДНФ, СКНФ, построить многочлен Жегалкина.

2. Для заданной булевой функции f x1, x2 , x3 , x4 V 4,5,6,7,10,11,13 :

а) составить таблицу истинности;

б) составить СДНФ и минимизировать методом Квайна;

в) представить результат в скобочной форме;

г) построить логическую схему, используя полученную минимальную функцию и сделать проверку по таблице истинности.

z | x y 0

4. Составить систему уравнений с булевыми переменными и найти ее решение.

1)Либо работает агрегат «в», либо работает агрегат «с».

2)Неверно, что если работает агрегат «а», то работает агрегат «в».

3)Либо работает агрегат «в», либо работает агрегат «d».

4) Или работает агрегат «а», или агрегат «в», или оба вместе. 5. Решить задачу:

Сколькими способами можно пронумеровать грани куба?

Вариант 26

1. Проверить, верно ли тождество: x ( y z) (x y) (x z)

(если тождество не верно, то все задания делать по левой части)

а) используя определения операций над множествами

б) с помощью алгебры логики.

Изобразить результат на кругах Эйлера. Соответствующую булеву функцию привести к СДНФ, СКНФ, построить многочлен Жегалкина.

2. Для заданной булевой функции f x1, x2 , x3 , x4 V 3,5,7,8,11,12,15 :

а) составить таблицу истинности;

б) составить СДНФ и минимизировать методом Квайна;

в) представить результат в скобочной форме;

г) построить логическую схему, используя полученную минимальную функцию и сделать проверку по таблице истинности.

x y z 1

3. Решить систему логических уравнений: y 1 0

z | x y 0

4. Составить систему уравнений с булевыми переменными и найти ее решение.

1)Либо работает агрегат «в», то работает агрегат «d».

2)Неверно, что работает агрегат «а» или работает агрегат «в».

3)Агрегат «а» работает тогда и только тогда, когда работает агрегат «d».

4) Если работает агрегат «в», то работает агрегат «с».

5) Либо работает агрегат «а», либо работает агрегат «с».

5. Решить задачу:

Сколько словарей из двух иностранных языков необходимо издать, чтобы можно было непосредственно выполнять технические переводы с любого из десяти иностранных языков на другой язык?

Вариант 27

1. Проверить, верно ли тождество: x ( y z) (x y) (x z)

(если тождество не верно, то все задания делать по левой части)

а) используя определения операций над множествами

б) с помощью алгебры логики.

Изобразить результат на кругах Эйлера. Соответствующую булеву функцию привести к СДНФ, СКНФ, построить многочлен Жегалкина.

2. Для заданной булевой функции f x1, x2 , x3 , x4 V 7,8,9,10,11,12,15 :

а) составить таблицу истинности;

б) составить СДНФ и минимизировать методом Квайна;

в) представить результат в скобочной форме;

г) построить логическую схему, используя полученную минимальную функцию и сделать проверку по таблице истинности.

x y z 1

4. Составить систему уравнений с булевыми переменными и найти ее решение.

1) Неверно, что работает агрегат «с» или работает агрегат «d».

2) Либо работает агрегат «в», либо работает агрегат «с».

3) Неверно, что если работает агрегат «а», то работает агрегат «в».

4) Агрегат «в» работает тогда и только тогда, когда работает агрегат «d».

5. Решить задачу:

В пространстве заданы 12 точек, каждые три из которых не лежат на одной прямой, и никакие 4 не лежат в одной плоскости. Сколько различных плоскостей через них можно провести?

Решение типового варианта

Задача 1. Выразить данную операцию над множествами через объединение, пересечение и дополнение: A B C A B A C

а) используя определения операций над множествами

б) с помощью алгебры логики.

Изобразить результат на кругах Эйлера. Соответствующую булеву функцию привести к СДНФ, СКНФ, построить многочлен Жегалкина.

Решение.

Проверить справедливость тождества

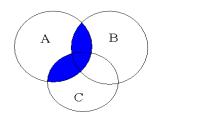
а) на кругах Эйлера

б) с помощью алгебры логики.

A B C A B A C

Решение

а) Отметим на кругах Эйлера соответствующую область:

б) Пусть U – универсум для множеств A, B,C . Рассмотрим предикаты принадлежности X x A , Y ( y B), Z (z C) . С использованием таблицы соответствия теоретико-множественных и логических операций:

задача сводится к проверке справедливости тождества

X Y Z X Y X Z .

Составляем таблицу истинности для левой и правой частей:

Из таблицы истинности видно, что тождество верно. Возможны другие способы доказательства, например использование тождественных преобразований логических формул (в данном случае тождество представляет собой дистрибутивность конъюнкции относительно дизъюнкции).

Проверьте, будут ли эквивалентны следующие формулы двумя способами. Приведите первую формулу к СДНФ, СКНФ, постройте многочлен Жегалкина. Какой теоретико-множественной операции соответствует первая формула?

x y z и x y x z .

Способ 1. Проверка по таблице истинности

Из таблицы истинности видим, что формулы эквивалентны.

Способ 2. Метод алгебраических преобразований

Сучѐтом того, что x y x y , получаем

xy z x y z x y z .

x y x z x y x z x y x z

x x z y x z x y z.

Формулы эквивалентны

Воспользовались законом де Моргана, ассоциативностью и коммутативностью дизъюнкции, дистрибутивностью дизъюнкции относительно конъюнкции и законом исключѐнного третьего.

СДНФ и СКНФ построим с помощью таблицы истинности. Для наглядности при построении СДНФ используем двойственную функцию