
Otchet_5
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра РАПС
отчет
по лабораторной работе №5
по дисциплине «Информатика»
Тема: Работа с векторами и матрицами
Студент гр. 2493 пк 14 |
|
Керро Е.Р. |
Преподаватель |
|
Пожидаев А.К. |
Санкт-Петербург
2021
Цель работы.
На примере практического задания освоить методы работы с матрицами в математическом пакете.
Ход работы.
Задание: решить линейную систему уравнений 3–го порядка. Коэффициенты задать самим (Решение проверить вручную, применив один из численных методов). Найти собственные значения и вектор квадратной матрицы А.
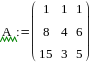
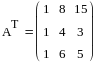
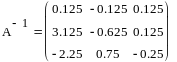
![]()
![]()
![]()
![]()
![]()
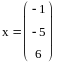
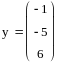
![]()
![]()

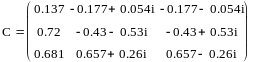
Для начала прописываем коэффициенты при искомых переменных в матрицу A. Затем значения суммы искомых переменных в вектор B. Решение системы уравнений которая задаётся данными вектором и матрицей будет искаться по формуле A-1B или же при помощи специальной функции lsolve, входящей в пакет MathCad. Получим решения и проверим их вручную.
Запишем систему в виде:
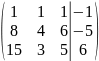
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен (1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ - (А*В)/РЭ
РЭ - разрешающий элемент (1), А и В - элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
В итоге получаем:
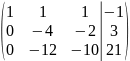
Разрешающий элемент равен (-4). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
В итоге получаем:
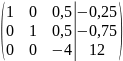
Разрешающий элемент равен (-4). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
В итоге получаем:

x1=1.25
x2=0.75
x3=-3
Также мы можем найти собственные значения матриц при помощи функции eigenval. А функцию eigenvec можно использовать для поиска собственных векторов.
Возможны также операции транспонирования и возведения в степень.
Выводы.
Математический пакет Matlab незаменим при работе с матрицами, с его помощью мы можем устанавливать важные сведения о них. Он может быть использован для решения больших систем линейных уравнений, что является крайне полезным при проведении научной деятельности.
