
лабаинф4керро
.doc
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
КАФЕДРА РАПС
отчет
по лабораторной работе №4
по дисциплине «Информатика»
Тема: Решение дифференциальных уравнений
Студент гр. 2493 к.№14 |
|
Керро Е.Р. |
Преподаватель |
|
Пожидаев А.К. |
Санкт-Петербург
2022
Задание: Найти функцию у(х), удовлетворяющую дифференциальному уравнению
Исходные данные:
Д ифференциальное
уравнение
ифференциальное
уравнение
Начальное значение функции y0 = 0
Начальное значение интегрирования а = 0
Конечное значение интегрирования b = 12π
Число шагов интегрирования К = 20
Математические формулы:
Создадим функцию Т(х,у), которая вычисляет значение производной при заданных значениях независимой переменной и неизвестной функции:
T(x, y) := –y0 + x∙cos(x)
Вычислим
численное решение уравнения при помощи
функции rkfixed,
подставив известные нам данные для
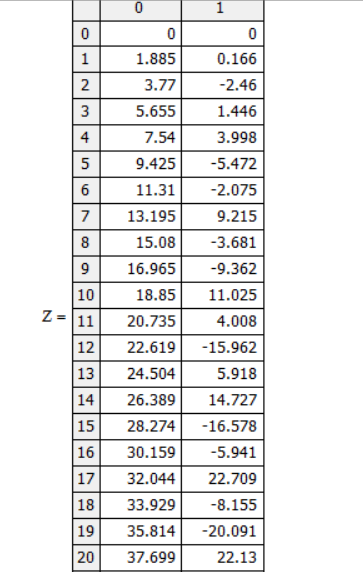
решения. Z:=
rkfixed(y,a,b,K,T).
Результат вычислений – матрица Z
с двумя столбцами, первый из которых
содержит значения независимой переменной,
а второй —соответствующие значения
функции.
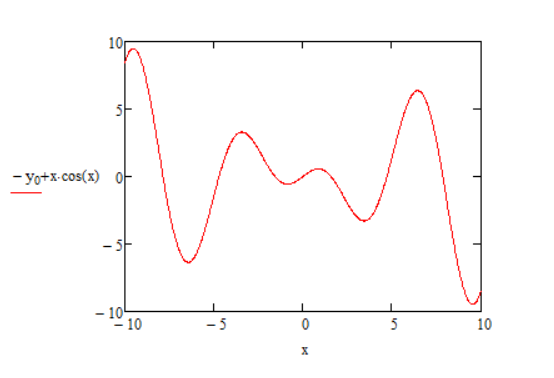
Построим двумерный график полученного решения с помощью Вставка > График > Х-У график.
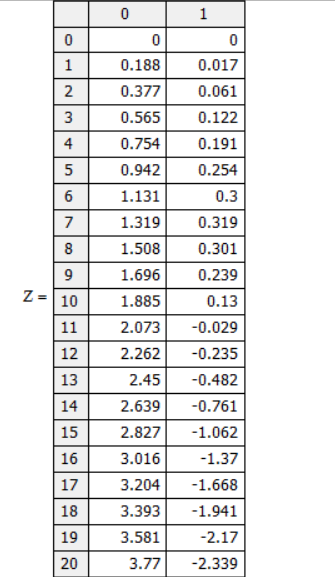
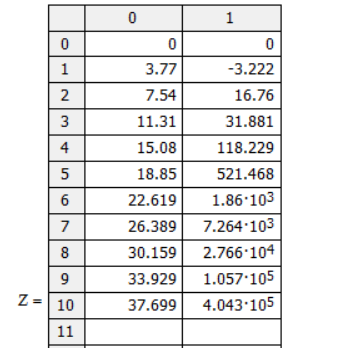
Изменяя число шагов на которое делится интегрирование мы можем заметить изменения в каждом из столбце матрицы.
Число
шагов 200:
Число
шагов 10:
Выводы:
