
Шпаргалка Раздел 4 Математическая статистика
.docxВыборка
Выборка
– это последовательность
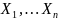 независимых одинаково распределенных
с.в., распределение каждой из которых
совпадает с распределением генеральной
совокупности.
независимых одинаково распределенных
с.в., распределение каждой из которых
совпадает с распределением генеральной
совокупности.
n – объем выборки – число элементов в выборке
Генеральная совокупность.
Генеральная совокупность – это с.в. X(ω), т.е. множество всех возможных ее значений или все теоретически возможные результаты наблюдения (опыта)
Реализация выборки.
Реализация выборки – это конкретные значения выборки полученные в результате наблюдений: .
Выборочный метод статистического исследования предполагает, что на основе выборки можно сделать заключение о генеральной совокупности.
Ранг элемента выборки.
Ранг – номер элемента в вариационном ряду (если есть несколько одинаковых элементов, то считается средний ранг).
Вариационный ряд выборки
Ранжирование
– расположение результатов наблюдения
в порядке неубывания. Результат
ранжирования – вариационный
ряд:
x(1),…,x(n),
x(1)=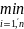 xi,
x(n)=
xi,
x(n)=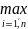 xi,
xi,
Размах выборки и интервал варьирования
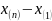 – размах выборки
– размах выборки
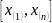 – интервал
варьирования
– интервал
варьирования
Выборочное среднее
Выборочное
среднее :
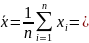
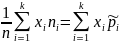
Для
группированных данных :
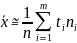
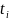 – центр
i-го
интервала группировки.
– центр
i-го
интервала группировки.
Выборочная дисперсия
Выборочная
дисперсия:
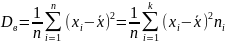
Для
группированных данных:
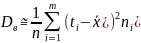
Несмещенная выборочная дисперсия
Несмещенная (исправленная выборочная дисперсия:
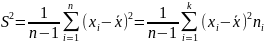
Эмпирическая функция распределения
Статистическая
(эмпирическая, выборочная) функция
распределения с.в. X – это функция
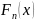 ,
равная доле таких значений
,
равная доле таких значений
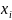 , что
, что
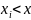 :
:
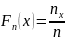
где
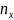 – число наблюдений <
– число наблюдений <
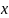
Полигон частот
Полигоном
частот
называют ломаную, отрезки которой
соединяют точки с координатами (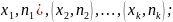

Гистограмма
Гистограмма
частот – столбчатая диаграмма с
основаниями длины h
и высотами
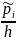
![]()
Выборочные квантили

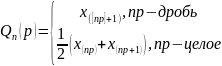
Статистическая оценка
Оценкой
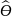 параметра
параметра
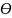 теоретического распределения называют
его приближенное значение, зависящее
от данных выбора, т.е. оценка есть
некоторая функция от результатов
наблюдений (статистика):
=
теоретического распределения называют
его приближенное значение, зависящее
от данных выбора, т.е. оценка есть
некоторая функция от результатов
наблюдений (статистика):
=
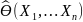 .
.
Свойства точечных оценок
1. Состоятельность
2. Несмещенность
3. Эффективность
Состоятельность оценки
Оценкой
параметра
называется состоятельной, если она
сходится по вероятности к оцениваемому
параметру при
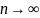
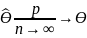 ,
т.е.
,
т.е.
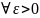
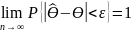
Несмещенность оценки.
Оценка
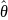 параметра
параметра
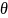 называется несмещенной, если она в
среднем совпадает с
,
т.е. М
называется несмещенной, если она в
среднем совпадает с
,
т.е. М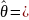
Эффективность оценки.
Несмещенная оценка параметра называется эффективной, если она имеет наименьшую дисперсию среди всех несмещенных оценок параметра
Метод моментов.
Идея: приравнивание теоретических и выборочных моментов.
Если необходимо оценить параметров получим систему:
MX
=
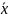 =
=
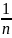
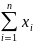
DX
=
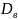 =
=
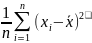
…
M(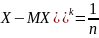
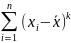
Метод максимального правдоподобия
Идея: найти максимум функции правдоподобия, т.е. подобрать такие значения параметров распределения, при которых выборка наиболее правдоподобна
Интервальное оценивание
При интервальном оценивании указывается интервал, в который с заданной вероятностью попадает параметр
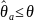 ≤
≤
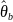
Обычно
–
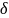 ≤
≤
+
≤
≤
+
Этот интервал называется доверительным интервалом, а вероятность называется доверительной вероятностью или надежностью оценки ( обозначается ƴ), величина α = 1 - ƴ - уровнем значимости оценки.
P( ≤ ) = 1 – α = ƴ
Обычно уровень значимости α = 0,01 ; 0,05 ; 0,1
Уровень значимости при интервальном оценивании
Надёжностью оценки (обозначается ), величина =1- - уровнем значимости оценки.
P( ≤ ) = 1 – α = ƴ
Обычно уровень значимости =0,01;0,05;0,1.
Статистическая гипотеза
Статистической гипотезой Н называется предположение относительно параметров или вида распределения случайной величины
Ошибки первого и второго рода при проверке гипотезы
Ошибка первого рода – отвергается нулевая гипотеза, когда она на самом деле верна. P(H1|H0)=α
Ошибка второго рода – отвергается альтернативная гипотеза, когда она на самом деле верна. P(H0|H1)=β
Общая схема проверки гипотез
1. Располагая выборкой Х1, …, Хn, формулируют нулевую (Н0) и альтернативную (Н1) гипотезы;
2. Назначается уровня значимости α (стандартные значения α: 0.1, 0.05, 0.01);
3. Выбирается статистика критерия Tn=T(Х1, …, Хn) (тип критерия). Обычно из перечисленных ниже: U – нормальное распределение, X2 – распределение Пирсона, t – распределение Стьюдента, F – распределение Фишера-Снедекора;
4.
По статистике критерия Tn
определяют критическую область S
(и
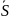 ).
Для ее определения достаточно найти
критическую точку tкр,
т.е. границу (или квантиль), отделяющую
область S
от
;
).
Для ее определения достаточно найти
критическую точку tкр,
т.е. границу (или квантиль), отделяющую
область S
от
;
5.Сравнение табличных и вычисленных значений статистики критерия.
Критерий согласия Х2 Пирсона
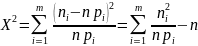
Эта статистика при имеет Х2 распределения с k=m-r-1 степенями свободы, где m – число групп (интервалов) выборки, r – число параметров предполагаемого распределения.
Критерий согласия Колмогорова
Является наиболее простым критерием согласия. Он связывает эмпирическую функцию распределения F*n(x) с функцией FX(x) непрерывной случайной величины Х. Гипотезы: Н0:FX(x)=F0(x) Н1:FX(x)≠F0(x)
Статистика Колмогорова имеет вид:
Dn=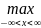 |F*n(x)-F0(x)|
|F*n(x)-F0(x)|
Эта
статистика, умноженная на
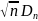 при
имеет распределение Колмогорова
независимо от распределения с.в. Х:
при
имеет распределение Колмогорова
независимо от распределения с.в. Х:
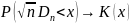 ,
где К(х) – функция распределения
Колмогорова, для которой составлена
таблица, которую можно использовать
для расчетов уже при n>=20
,
где К(х) – функция распределения
Колмогорова, для которой составлена
таблица, которую можно использовать
для расчетов уже при n>=20
α |
0,1 |
0,05 |
0,02 |
0,01 |
0,001 |
x0 |
1,224 |
1,358 |
1,520 |
1,627 |
1,950 |
