Шпаргалка Раздел 2 Одномерные случайные величины

1. Случайная величина

Случайной величиной называется величина, которая в результате опыта может принять одно конкретное значение причем заранее неизвестно, какое именно

2. Дискретная случайная величина

Называется вещественная функция, заданная на вероятностном пространстве элементарных событий

3. Непрерывная случайная величина

Непрерывная с.в. принимает все числовые значения из некоторого конечного или бесконечного промежутка

Её невозможно описать таблицей(из-за бесконечного и несчётного количества значений)

4. Закон распределения вероятностей

Рассмотрим дискретную с.в. Х, которая может принимать значения Х = х1,…,хn. Тогда закон распределения вероятностей указывает вероятность каждого возможного значения:

Р(X = ) = , i = (палка над ними)

Причем

С.в. будет полностью описана, если установлен ее закон распределения вероятностей.

Закон распределения можно задавать в виде таблицы – ряд распределения или графика – многоугольник распределения.

5. Функция распределения вероятностей

Функцией распределения вероятностей с.в. Х называется функция

Функция распределения может быть построена как для дискретных, так и для непрерывных с.в. и полностью характеризует с.в. с вероятностой точки зрения.

6. Свойства функции распределения вероятностей

1. - монотонно неубывающая функция, т.е. если х1<x2, то ≤

2. ,

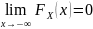3. –непрерывна слева, т.е.

7. Плотность распределения вероятностей

Пусть Х – непрерывная с.в., тогда её плотностью распределения вероятностей называется функция т.ч.

= (t) dt

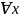,для который Ǝ (x)

=

P(a< X< b) =

Т.е. плотность распределения вероятностей – это вероятность, приходящаяся на единицу длины.

График плотности вероятностей называют кривой распределения.

8. Свойства плотности распределения вероятности

1.Неотрицательность: ≥ 0

2.Нормированность (x) dx = 1

3.

9. - непрерывная случайная величина,

P(a < X < b) = P(a ≤ X ≤ b) = P ( a ≤ X < b) = P(a < X ≤ b) = P (X<b) – P(X<a) = -

10. - дискретная случайная величина

P(a ≤ X < b) = P(X < b) – P(X < a) = -

11. Квантиль

Квантиль – значение, которое заданная случайная величина не превышает с фиксированной вероятностью.

– называется медианой

– называется нижняя квартиль

– называется верхняя квартиль

Квантиль уровня р с.в. Х называется решение уравнения 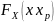= р

12. Мода

Модой д.с.в.называется ее значение, принимаемое с наибольшей вероятностью по сравнению с двумя соседними значениями, обозначается через -точка максимума (локального)плотности fX(x)

13. Медиана

Медианой н.с.в. Х называется такое ее значение , для которого

P {X < } = P{X > =

Т.е. одинаково вероятно, окажется ли с.в. Х меньше или больше

14. Математическое ожидание дискретной с.в.

Математическим ожиданием дискретной с.в. Х с законом распределения = P(X = ) называется число

MX = =

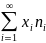
если этот ряд абсолютно сходится

15. Математическое ожидание непрерывной с.в.

Математическим ожиданием непрерывной с.в.Х с плотностью распределения (х) называется число

МХ =

если этот интеграл абсолютно сходится

16. Свойства математического ожидания

1. Mc = c

2. M(cX) = cMX

3.M(c+X) = c + MX

4.M|X| ≤ |MX|

5.M( = M +

6.Если с.в. – независимы, то М( =М М

17. Дисперсия

Дисперсией с.в. Х называется математическое ожидание квадрата ее отклонения от математического ожидания:

DX = M =M -

Если с.в. Х дискретная, то

DX =

Если с.в. Х непрерывная, то

BX = dx=

Дисперсия характеризует разброс значений с.в. относительно ее математического ожидание, ее размерность совпадает с размерностью квадрата с.в.

18. Свойства дисперсии

1.Dc = 0

2.D(cX) = DX

3.D(c+X)=DX

4.Если Если с.в. – независимы, то D( =М М

19. Среднеквадратическое отклонение

Среднеквадратическим отклонением с.в. Х называется

σX =

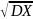
Среднеквадратическое отклонение тоже характеризует разброс значений с.в., но его размерность совпадает с размерностью с.в.

20. Центральный и абсолютный центральный момент k-го порядка

Центральный момент k-го порядка: M

Абсолютный центральный момент k-го порядка:

M

Размерность моментов к-го порядка совпадает с к-ой степенью размерности с.в. Часто для удобства расчётов используют нормированные момента, не имеющие размерности.

Нормированный момент к-го порядка имеет вид:

21. Асимметрия

Нормированный центральный момент 3-го порядка называется ассиметрией:

=

Ассиметрия характеризует ассиметричность распределения (для симметричных распределений она равна 0)

22. Эксцесс

Нормированный центральный момент 4-го порядка называется эксцессом:

=

Эксцесс характеризует выраженность вершины распределения. Нормировка (-3) выбрана т.ч. для нормального закона распределения эксцесс был равен нулю.

23. Биномиальное распределение

Случайная величина Х – число успехов в схеме Бернулли имеет биномиальное распределение с законом:

P(X = m) = , m = 0, n (черточка над ними)

0 < p < 1

MX = np DX = npq

24. Распределение Пуассона

Закон редких событий.Является предельным для биномиального распределения

Случайная величина Х – число успехов в схеме Бернулли, в которой

n , p 0, np = = const

имеет распределение Пуассона с законом:

P(X = m) = , m = 0,1,2…

MX = DX =

25. Геометрическое распределение

Случайная величина Х – число испытаний до первого успеха в схеме Бернулли имеет геометрическое распределение с законом:

P(X=m) = p, m = 1,2,3…, 0<p<1

MX = 1/p, DX = q/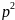

26. Равномерное распределение

Если нет информации о наиболее или наименее вероятных значения с.в., то она полагается равномерно распределенной с плотностью распределения

0, else

MX = (a+b)/2 DX = /12

27. Экспоненциальное распределение

Моделирует время между двумя последовательными совершениями одного и того же события:

= { a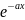 , x ≥0, a >0

{ 0, else

MX = 1/a DX = 1/

28. Нормальное распределение

Одно из наиболее распространенных распределений имеет плотность:

= , σ > 0

MX = m, DX =

Если в нормальном распределении m = 0, σ = 1, то оно называется стандартным.

29. Функция распределения для нормального закона

Ф(х) =

30. Правило «трех сигм»

P(|X-m| < 3σ) = 2 ≈0.9973

Т.е. практически достоверно, что все значения нормально распределенной с.в. лежат в интервале (m - 3σ, m + 3σ)