Группа 3(26–39)

Группировка членов числового ряда. Теорема Римана (с доказательством). В противоположность переместительному свойству (которое имеет место лишь для абсолютно сходящихся рядов) сочетательным свойством обладает всякий сходящийся ряд.

Именно во всяком сходящемся ряде можно, не меняя по рядка членов, объединять их в какие угодно группы. Сложив члены внутри всех групп, получаем новый ряд. Он тоже сходится и его сумма — прежняя.

Пример 1. В сходящемся (по признаку Лейбница) ряде

можно сгруппировать члены следующим образом:

Сложив члены внутри групп, получим:

Этот знакоположительный ряд имеет ту же сумму, что и знакопеременный ряд (1).

Пример 2. В ряде (1) можно сгруппировать второй член с третьим, четвертый с пятым и т. д. Получим сходящийся ряд

имеющий ту же сумму.

Замечание. Обратное действие (раскрытие скобок) безусловно допустимо лишь в том случае, если после раскрытия скобок получается сходящийся ряд (тогда данный ряд — заведомо сходящийся). Однако возможен случай, когда данный ряд сходится, а после раскрытия скобок получается расходящийся ряд.

Пример 3. Ряд

(геометрическая прогрессия ) сходится и имеет сумму .

Если раскрыть скобки, то получим ряд

он расходится, так как частичные суммы с четными номерами имеют прежнии предел  а с нечетными номерами — предел .

Пример 4. Рассмотрим ряд

Его можно представить в виде

Здесь можно раскрыть скобки, так как полученный ряд

— сходящийся. Действительно, всякая частичная сумма  равна единице, а частичная сумма

стремится к единице. Сумма  ряда (8) является также суммой ряда (6):

Пусть S – произвольное число (конечное или бесконечное). Тогда можно так переставить местами члены условно сходящегося знакопеременного ряда, что его сумма будет равна S.

Доказательство. Так как ряд A условно сходится, то ряды P, Q расходятся (теоремы о структуре знакопеременного ряда). Пусть для определенности S>0. Переставляем в начало ряда столько положительных членов, чтобы их сумма стала больше S, Теперь переставляем столько отрицательных членов, чтобы частичная сумма ряда стала бы меньше S. Повторяем этот процесс. Процесс осуществим для любого S, так как ряды P, Q расходятся (т.е. повторением членов можно набрать любую их сумму). С другой стороны, частичная сумма сконструированного ряда сходится именно к S. В сконструированном ряде  - тот член ряда, добавление которого меняет знак . так как знакопеременный ряд условно сходится.

Сам ход доказательства напоминает добавление положительных членов – гирь на одну чашку весов, пока весы не покажут вес, больший S. Последний член – гиря  . Затем добавление на другую чашку весов столько отрицательных – членов (вернее гирь, весом, равным модулям этих членов), чтобы весы показали вес, меньшийS. Процесс повторяется. Вес гирь, вызывающих переход указателя весов через S, убывает до нуля, так как для условно сходящегося ряда выполняется необходимый признак сходимости. Поэтому  .

27. Переместительное свойство абсолютно сходящегося ряда. (Теорема Коши, с доказательством).

Если данный ряд сходится абсолютно, то любой ряд, полученный из данного посредством некоторой перестановки членов, также сходится абсолютно и имеет ту же сумму, что и данный ряд.

Д о к а з а т е л ь с т в о. Пусть ряд сходится абсолютно и сумма ряда равна S. Пусть, далее, 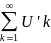(2) ряд, полученный из ряда (1) посредством некоторой перестановки членов.

Достаточно доказать, что для любого ε > 0 найдется номер N такой, что при n≥N | -S|< ε

Фиксируем произвольные ε > 0 Так как ряд (1) сходится абсолютно и имеет сумму, равную S, то для выбранного ε > 0 можно указать номер

и 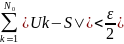. Выберем теперь номер N столь большим, чтобы любая частичная сумма S’n ряда (2) с номером n, превосходящим N, содержало все первые членов ряда (1).

28. Интеграл Лебега. Функция Дирихле.

Интеграл Лебега — это обобщение интеграла Римана на более широкий класс функций.

Все функции, определённые на конечном отрезке числовой прямой и интегрируемые по Риману, являются также интегрируемыми по Лебегу, причём в этом случае оба интеграла равны. Однако существует большой класс функций, определённых на отрезке и интегрируемых по Лебегу, но неинтегрируемых по Риману. Также интеграл Лебега может иметь смысл для функций, заданных на произвольных множествах (интеграл Фреше).

Идея построения интеграла Лебега состоит в том, что вместо разбиения области определения подынтегральной функции на части и составления потом интегральной суммы из значений функции на этих частях, на интервалы разбивают её область значений, а затем суммируют с соответствующими весами меры прообразов этих интервалов.

29. Гильбертово пространство L².

Ортонормированная система функций пространства L². Её свойства. Пространство L2 означает совокупность всех вещественных измеримых (определение измеримости см. в [7]) функций х(t), заданных и суммируемых с квадратом на отрезке [а, b]. Суммируемость с квадратом означает, что

b

∫x2 (t)dt < ∞,

a

т. е. что функция x2 (t) должна быть суммируемой. Ясно, что в L 2 входят, в частности, все ограниченные измеримые функции, заданные на [а, b], тем более входят все непрерывные функции.

Вместо отрезка [а, b] можно рассматривать любое измеримое множество с конечной мерой (см. [7]) в любом евклидовом пространстве Rn .

Норма в L2 вводится по формуле

 x  =  ∫b x2 (t) dt .

a

При таком определении все аксиомы нормы выполняются. Таким образом, L2

– нормированное пространство. Кроме того, это пространство является банаховым и сепарабельным.

Для любого элемента x L2 можно одновременно рассматривать его нормы в пространствах L2 и L1:   x  L2 и   x  L1 . Эти нормы связаны следующим

соотношением:

 x  L1 ≤  b −a   x  L2 .

89

Определим в L2 скалярное произведение функций x, y L2 как интеграл от произведения этих функций по отрезку [a, b]:

(x, y) = ∫b x(t) y(t)dt .

a

Следовательно, норма в L2 порождается скалярным произведением, и, поскольку L2 полно, оно является гильбертовым пространством. Кроме того, оно бесконечномерно.

Итак, L2 – бесконечномерное, сепарабельное, гильбертово пространство.

По теореме 5.11 пространство L2 изоморфно и изометрично пространству l 2. Также по теореме 5.12 сохраняется и величина скалярного произведения. Но так как теорема 5.11 применима к любому абстрактному сепарабельному бесконечномерному гильбертову пространству H, то сопоставляя каждому элементу h H вместо соответствующего ему элемента x l 2

соответствующий элементу x элемент y L2, мы установим алгебраический изоморфизм между H и L2 с сохранением величины нормы и скалярного произведения. Таким образом, можно говорить, что пространство l2 представляет функциональную реализацию абстрактного сепарабельного бесконечномерного гильбертова пространства.

31. Понятие общего ряда Фурье.

Понятие общего ряда Фурье связано с разложением бесконечномерного евклидова пространства по ортонормированной системе. Будем рассматривать бесконечномерное евклидово пространство, т. е. линейное пространство, в котором имеется в том числе и бесконечно большое число независимых элементов , с точки зрения функций тригонометрической системы. Рядом Фурье элемента F по ортонормированной системе   называется ряд  , где  .   называется коэффициентом Фурье элемента F.

32. Свойства n-ой частичной суммы ряда Фурье. Тождество и неравенство Бесселя. Равенство Парсеваля.

Ги́льбертово простра́нство — обобщение евклидова пространства, допускающее бесконечную размерность и полное по метрике, порождённой скалярным произведением. Названо в честь Давида Гильберта.

Важнейшим объектом исследования в гильбертовом пространстве являются линейные операторы. Само понятие гильбертова пространства сформировалось в работах Гильберта и Шмидта по теории интегральных уравнений, а абстрактное определение было дано в работах фон Неймана, Риса и Стоуна по теории эрмитовых операторов.

В математике неравенство Бесселя — утверждение о коэффициентах элемента {\displaystyle x}x в гильбертовом пространстве касательно ортонормированной последовательности.

33. Единственность разложения функции в ряд Фурье.

Если функция раскладывается в ряд Фурье, то это разложение единственно.

Если функция , заданная и непрерывная на отрезке, раскладывается в тригонометрический ряд, то коэффициенты его определяются единственным образом.

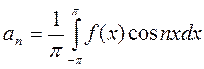
Если непрерывная на отрезке  функция раскладывается в тригонометрический ряд, то это обязательно ряд Фурье.

Пусть  задана на отрезке  и в каждой точке этого промежутка имеет конечную производную . Тогда ряд Фурье этой функции сходится на всей числовой оси, причём сумма его равна в точках , для которых и

(11)

Сходимость к нулю коэффициентов тригонометрического ряда Фурье. Многие процессы, происходящие в природе и технике, обладают свойством повторяться через определенные промежутки времени. Такие процессы называются периодическими и математически описываются периодическими функциями. К таким функциям относятся sin(x), cos(x), sin(wx), cos(wx). Сумма двух периодических функций, например, функция вида  , вообще говоря, уже не является периодической. Но можно доказать, что если отношение w₁/w₂ – число рациональное, то эта сумма есть периодическая функция.

Простейшие периодические процессы – гармонические колебания – описываются периодическими функциями sin(wx) и cos(wx). Более сложные периодические процессы описываются функциями, составными либо из конечного, либо из бесконечного числа слагаемых вида sin(wx) и cos(wx). Рассмотрим функциональный ряд вида:

. (1)

Этот ряд называется тригонометрическим; числа а₀,b₀,a₁,b₁,а₂,b₂…,a_n,b_n,… называются коэффициентами тригонометрического ряда. Ряд (1) часто записывается следующим образом:

. (2)

Так как члены тригонометрического ряда (2) имеют общий период  , то и сумма ряда, если он сходится, также является периодической функцией с периодом .

Допустим, что функция f(x) есть сумма этого ряда:

. (3)

В таком случае говорят, что функция f(x) раскладывается в тригонометрический ряд. Предполагая, что этот ряд сходится равномерно на промежутке  , можно определить его коэффициенты по формулам:

,  , . (4)

Коэффициенты ряда, определенные по этим формулам, называются коэффициентами Фурье.

Тригонометрический ряд (2), коэффициенты которого определяются по формулам Фурье (4), называются рядом Фурье, соответствующим функции f(x).

Таким образом, если периодическая функция f(x) является суммой сходящегося тригонометрического ряда, то этот ряд является ее рядом Фурье. Формулы (4) показывают, что коэффициенты Фурье могут быть вычислены для любой интегрируемой на промежутке  -периодической функции, т.е. для такой функции всегда можно составить ряд Фурье. Но будет ли этот ряд сходиться к функцииf(x) и при каких условиях?

Напомним, что функция f(x), определенная на отрезке [a;b], называется кусочно-гладкой, если она и ее производная имеют не более конечного числа точек разрыва первого рода.

Следующая теорема дает достаточные условия разложимости функции в ряд Фурье.

Теорема Дирихле. Пусть  -периодическая функцияf(x) является кусочно-гладкой на  . Тогда ее ряд Фурье сходится кf(x) в каждой ее точке непрерывности и к значению 0,5(f(x+0)+f(x-0)) в точке разрыва.

Пример1.

Разложить в ряд Фурье функцию f(x)=x, заданную на интервале  .

Решение. Эта функция удовлетворяет условиям Дирихле и, следовательно, может быть разложена в ряд Фурье. Применяя формулы (4) и метод интегрирования по частям  , найдем коэффициенты Фурье:

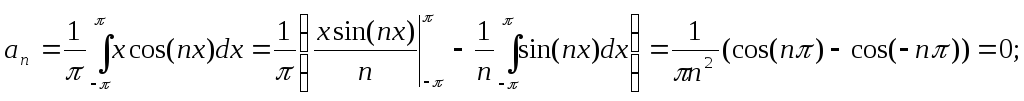
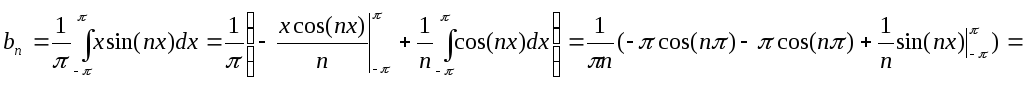
Т.к.  .

Таким образом, ряд Фурье для функции f(x) имеет вид:

35. Условия Дирихле разложимости функции в тригонометрический ряд Фурье.

36. Разложение на произвольном промежутке. Комплексная форма тригонометрического ряда Фурье.