
УИРС 6пр
.docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное образовательное
учреждение высшего образования
«Юго-Западный государственный университет»
Практическая работа №6
По дисциплине: «Учебно-исследовательская работа студетов»
Тема: «Математическое моделирование»
Выполнил: Бунина А.В.
студент группы ИБ-01б
Проверил: Чеснокова А.А.
преподаватель
Курск, 2022
ЦЕЛЬ РАБОТЫ
Изучение математического моделирования для применения на практике.
ПРАКТИЧЕСКОЕ ЗАДАНИЕ
1. Дать пояснение сущности и перечислить требования, предъявляемые к математическому моделированию.
2. По своей теме подобрать или описать пример математического моделирования.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Сущность математического моделирования.
Сущность математического моделирования состоит в замене исходного объекта его "образом" - математической моделью - и дальнейшем изучении модели с помощью реализуемых на компьютерах вычислительно-логических алгоритмов. Этот "третий метод" познания, конструирования, проектирования сочетает в себе многие достоинства, как теории, так и эксперимента. Работа не с самим объектом (явлением, процессом), а с его моделью дает возможность безболезненно, относительно быстро и без существенных затрат исследовать его свойства и поведение в любых мыслимых ситуациях (преимущества теории).
Сама постановка вопроса о математическом моделировании какого-либо объекта порождает четкий план действий. Его можно условно разбить на три этапа: модель - алгоритм -программа (см. рисунок 1).
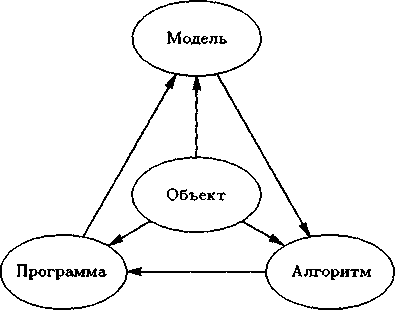
Рисунок 1 – Схема математического моделирования
На первом этапе выбирается (или строится) "эквивалент" объекта, отражающий в математической форме важнейшие его свойства - законы, которым он подчиняется, связи, присущие составляющим его частям, и т. д. Математическая модель (или ее фрагменты) исследуется теоретическими методами, что позволяет получить важные предварительные знания об объекте.
Второй этап - выбор (или разработка) алгоритма для реализации модели на компьютере. Модель представляется в форме, удобной для применения численных методов, определяется последовательность вычислительных и логических операций, которые нужно произвести, чтобы найти искомые величины с заданной точностью. Вычислительные алгоритмы должны не искажать основные свойства модели и, следовательно, исходного объекта, быть экономичными и адаптирующимися к особенностям решаемых задач и используемых компьютеров.
На третьем этапе создаются программы, "переводящие" модель и алгоритм на доступный компьютеру язык. К ним также предъявляются требования экономичности и адаптивности. Их можно назвать "электронным" эквивалентом изучаемого объекта, уже пригодным для непосредственного испытания на "экспериментальной установке" - компьютере.
Рассматривая вопрос шире, напомним, что моделирование присутствует почти во всех видах творческой активности людей различных "специальностей". Математическое моделирование плодотворно лишь при выполнении хорошо известных профессиональных требований:
четкая формулировка основных понятий и предположений,
апостериорный анализ адекватности используемых моделей,
гарантированная точность вычислительных алгоритмов и т. д.
ВЫПОЛНЕНИЕ РАБОТЫ
Тема: математическая модель процесса переключения передач. Рассмотрим процесс переключения передач с перекрытием с низшей передачи на высшую в коробках передач с неподвижными осями валов на примере схемы элементарного узла коробках передач, когда фрикционные муфты выключаемой передачи установлена на ведомом валу, а фрикционные муфты включаемой передачи на ведущем валу (рис. 2). Здесь шестерни 4 и 5 установлены на валах свободно и могут быть связаны с ним с помощью фрикционные муфты ФK1 и ФK соответственно. Шестерни 3 и 6 жестко связаны с валами. Пара шестерен 3 и 4 и ФМ ФK1 образуют K 1 передачу, а пара шестерен 5 и 6 и ФМ Фк – K передачу. При этом передаточные числа соответственно на низшей и высшей передаче в коробках передач:
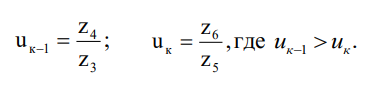
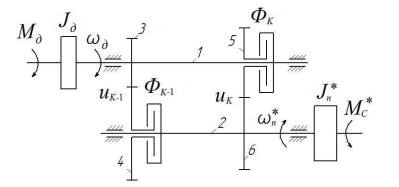
Рисунок 2 – Включение передачи
Запишем уравнения моментов соответственно для ведущего 1 и ведомого 2 валов в коробках передач, рассмотрев процесс переключения на основе двухмассовой динамической модели применительно к элементарному узлу КП с ФМ включаемой передачи на ведомом валу:
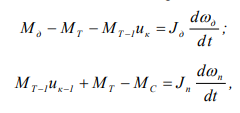
Согласно условию, что изменение угловой скорости двигателя d в период перекрытия не происходит, уравнения и примут вид:
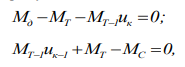
Получим уравнение для момента двигателя Мd будет иметь вид:
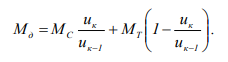
Напишем уравнения моментов случая, когда муфты расположены на ведомом валу:
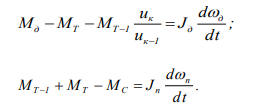
Когда фрикционные муфты включаемой и выключаемой передачи находится на ведущем валу дифференциальные уравнения будут иметь вид:
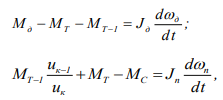
Определим характер изменения момента М Т 1 на валу фрикционные муфты ФK1.
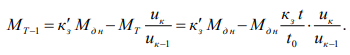
Таким образом, предложенная математическая модель переключения передач с различной степенью перекрытия является универсальной. Она позволяет выполнять расчеты работы переключения передач в коробки передач с различной степенью перекрытия и является справедливой для любого типа элементарного узла коробки передач.
Вывод: изучили математическое моделирование для применения на практике.
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
1. Буш, Г.Я. Рождение изобретательских идей./ Г.Я. Буш.- Рига: Лиесма, 1976,− 126 с.
2. Центр креативных технологий: [сайт]. URL: http://www.inventech.ru (дата обращения: 21.11.2022).
