
колды / Черевко С. ПР-30 лр 12
.pdf


Практическая часть:
Цель работы: Определение среднего размера частиц в микрогетерогенной системе с помощью оптического микроскопа с объект-микрометром, построение интегральной и дифференциальной кривых распределения частиц по размерам.
Определяющий размер – максимальное расстояние в горизонтальном направлении
Частицы SiO2 стержнеобразной формы
Измерены размеры частиц, мкм:
10,36; 13,11; 2,46; 2,76; 3,45; 3,3; 3,45; 7,76; 2,45; 2,59; 4,6; 2,01; 11,21; 2,3; 5,03; 4,4; 2,71; 5,04; 2,46; 2,3; 7,22; 3,02; 2,45; 3,31; 3,16; 7,91; 1,15; 1,59; 1,72; 3,45; 1,87; 1,87; 1,58; 1,3; 2,88; 4,03; 4,74; 10,06; 5,89; 3,75; 4,47; 2,74; 4,03; 1,44; 3,31; 3,32; 3,88; 2,73; 4,09; 3,24; 4,19; 4,33; 10,78; 1,87;4,32;6,62; 4,35; 5,6; 4,89; 4,89; 6,95; 4,19; 12,97; 5,89; 3,45; 3,74; 2,02; 2,73; 6,75; 2,16; 1,72; 2,59; 5,75; 2,02; 6,32; 2,44; 1,72; 2,59; 3,19; 0,86; 5,033,89; 6,75; 7,76; 2,91; 3,59; 5,03; 4,89; 3,59; 2,45; 6,62; 9,5; 3,31; 3,32; 3,64; 3,84; 4,75; 4,76; 4,6; 8,77; 9,05; 1,72; 6,75; 5,32; 2,16; 2,3; 5,47; 3,32; 17,16; 5,75; 3,3; 1,29; 5,32; 1,59; 3,59; 2,6; 3,3; 2,59; 3,02; 2,87; 5,89; 5,75; 8,77; 6,69; 5,93
Количество фракций: N=10
dmax = 17,16 мкм; dmin = 0,86 мкм
Расчеты:
Интервал размеров частиц:
h = (dmax - dmin)/N = (17,16-0,86)/10 = 1,63 мкм
r = h/4 = 0,4075 мкм
Расчет среднечисленного радиуса:
rn = Σ(ni*di/Σni) = 2,66 мкм
Расчет среднеповерхностного радиуса:
rs = Σ(ni*(di^3)/Σ(ni*(di^2))) = 4,13 мкм
Расчет среднемассового радиуса:
rw = Σ(ni*(di^4)/Σ(ni*(di^3))) = 4,97 мкм
Расчет степени полидисперсности: П = rn/ rw = 0,53
Расчет среднего радиуса частиц ri производится по формуле:
ri = 0,5*(dmin + h(i-1) + h/2)
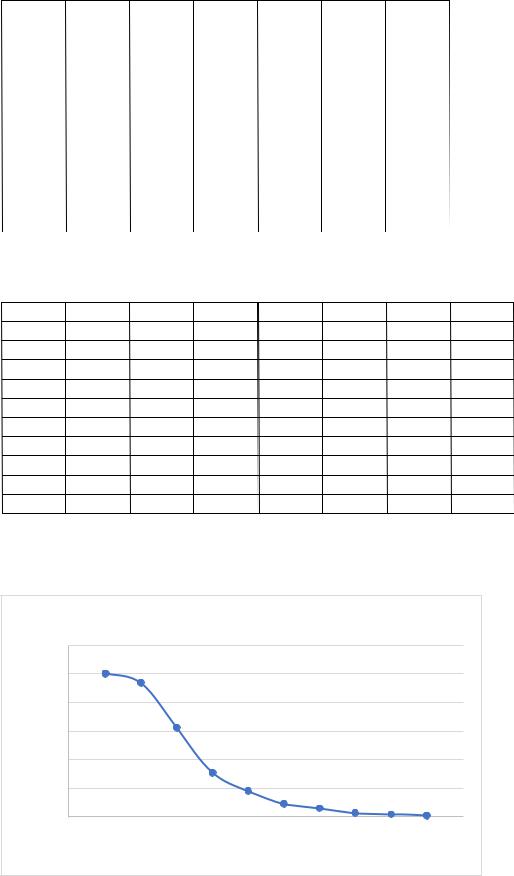
Таблица 2.12 Результаты дисперсного анализа:
i |
ri, мкм |
ni |
|
niri |
niri^2 |
niri^3 |
niri^4 |
1 |
0,8375 |
|
8 |
6,7 |
5,61125 |
4,699422 |
3,935766 |
2 |
1,6525 |
|
39 |
64,4475 |
106,4995 |
175,9904 |
290,8242 |
3 |
2,4675 |
|
39 |
96,2325 |
237,4537 |
585,917 |
1445,75 |
4 |
3,2825 |
|
16 |
52,52 |
172,3969 |
565,8928 |
1857,543 |
5 |
4,0975 |
|
11 |
45,0725 |
184,6846 |
756,745 |
3100,763 |
6 |
4,9125 |
|
4 |
19,65 |
96,53063 |
474,2067 |
2329,54 |
7 |
5,7275 |
|
4 |
22,91 |
131,217 |
751,5455 |
4304,477 |
8 |
6,5425 |
|
1 |
6,5425 |
42,80431 |
280,0472 |
1832,209 |
9 |
7,3575 |
|
1 |
7,3575 |
54,13281 |
398,2821 |
2930,361 |
10 |
8,1725 |
|
1 |
8,1725 |
66,78976 |
545,8393 |
4460,872 |
|
сумма |
|
124 |
329,605 |
1098,12 |
4539,165 |
22556,27 |
Таблицы 2.13 и 2.14 Исходные данные для построения кривых численного распределения частиц по размерам:
ri, мкм |
dQn, % |
Qn, % |
dQn/dr |
ri, мкм |
dQw, % |
Qw, % |
dQw/dr |
0,8375 |
6,451613 |
100 |
15,83218 |
0,8375 |
0,103531 |
100 |
0,254063 |
1,6525 |
31,45161 |
93,54839 |
77,18187 |
1,6525 |
3,877154 |
99,89647 |
9,514487 |
2,4675 |
31,45161 |
62,09677 |
77,18187 |
2,4675 |
12,90803 |
96,01932 |
31,67616 |
3,2825 |
12,90323 |
30,64516 |
31,66436 |
3,2825 |
12,46689 |
83,11128 |
30,5936 |
4,0975 |
8,870968 |
17,74194 |
21,76925 |
4,0975 |
16,67146 |
70,64439 |
40,91155 |
4,9125 |
3,225806 |
8,870968 |
7,916089 |
4,9125 |
10,447 |
53,97293 |
25,63681 |
5,7275 |
3,225806 |
5,645161 |
7,916089 |
5,7275 |
16,55691 |
43,52593 |
40,63045 |
6,5425 |
0,806452 |
2,419355 |
1,979022 |
6,5425 |
6,169574 |
26,96902 |
15,14006 |
7,3575 |
0,806452 |
1,612903 |
1,979022 |
7,3575 |
8,774347 |
20,79945 |
21,53214 |
8,1725 |
0,806452 |
0,806452 |
1,979022 |
8,1725 |
12,0251 |
12,0251 |
29,50945 |
Интегральные кривые распределения Qn=f(r), Qw=f(r) распределения частиц по числу и массе:
Qn, %
Qn=f(r)
120
100
80
60
40
20
0
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
r, мкм

Qw=f(r)
Qw, %
120
100
80
60
40
20
0
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
r, мкм
Дифференциальные кривые Qn/ r=f(r), Qw/ r=f(r) распределения частиц по числу и массе:
dQn/dr=f(r)
dQn/dr
90
80
70
60
50
40
30
20
10
0
0 |
2 |
4 |
6 |
8 |
10 |
12 |
r, мкм
Вывод:
Была выполнена лабораторная работа № 12 (2), в ходе которой были рассчитаны: среднечисленный радиус (rn = 2,66 мкм), среднеповерхностный радиус (rs = 4,13 мкм), среднемассового радиус (rw = 4,97 мкм) и полидисперсность: П = 0,53. Так как, rn<rs<rw, а П<1, можем сделать вывод, что система полидисперсная. По исходным данным были построены интегральные и дифференциальные кривые распределения частиц по размерам, их вид подтверждает полидисперсность системы.
