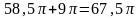Задача 3.6 В.17
.docxЗадача 3.6.Знайти площу фігури обмеженої лініями:
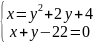
Обчислити об’єм тіла, одержаного обертанням навколо осі Оx фігури, що обмежена лініями.
y=0, при y>0
Розв’язання:
Обчислення площі
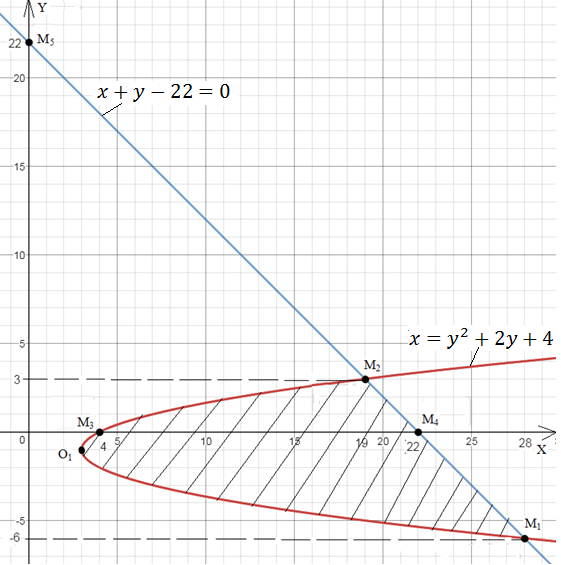
Побудуємо
фігуру , обмежену параболою
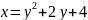 та
та
прямою
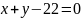
Шукаємо точки перетину заданих ліній між собою:
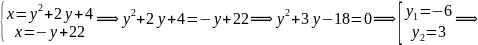
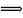 М1(28;
–6);
М2(19;3)
– точки перетину заданих ліній між
собою.
М1(28;
–6);
М2(19;3)
– точки перетину заданих ліній між
собою.
Шукаємо точки перетину заданих ліній з віссю Ох:
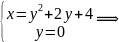 М3(4;
0)
М3(4;
0)
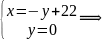 М4(22;
0)
М4(22;
0)
Шукаємо точки перетину заданих ліній з віссю Оу:
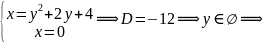 точок
перетину немає
точок
перетину немає
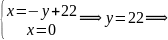 М5(0;22)
М5(0;22)
Знайдемо вершину параболи:
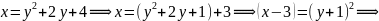 О1(3;
–1)
О1(3;
–1)
Для обчислення площі фігури найзручніше скористатись формулою:
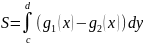
Отже, одержимо:

Знаходимо об’єм тіла обертання
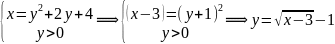
Об’єм тіла, утвореного обертанням фігури навколо осі Ох, обчислюється за формулою:
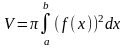
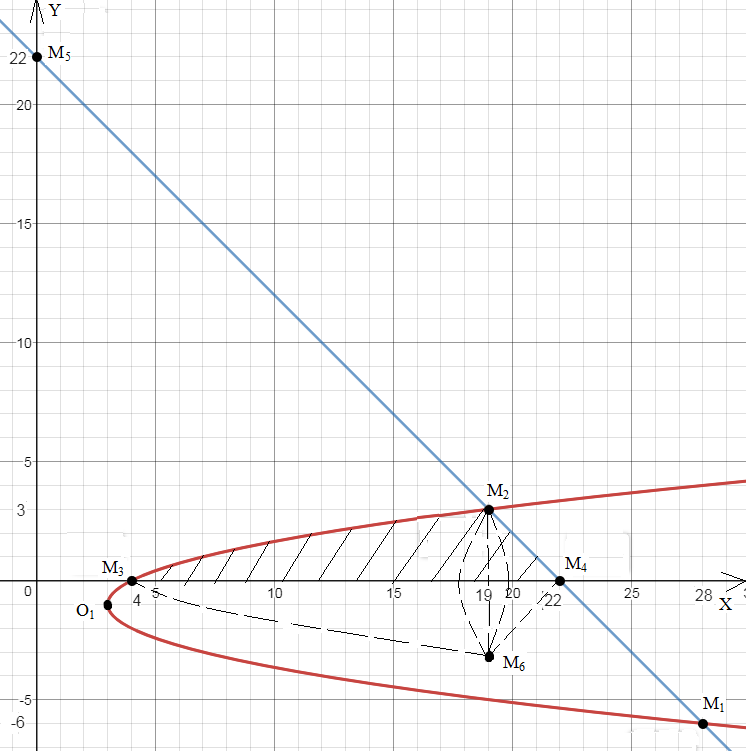
Знаходимо об’єм тіла обертання:

Знаходимо об’єм конуса М2М4М6:
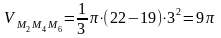
Отже, об’єм тіла обертанняМ3М2М4М6:
VМ3М2М4М6=