5 семестр / 10 вариант / рпз

Таким образом, выделяется зона «технологического заострения». Проводится линия [ ] до пересечения с графиком . Таким образом, определяется область допустимых значений по [ ].

Выбираем 1 = 0,4

2 = 0= 2 − радиус делительной окружности

= = 1 − − радиус скругления

0,3 12= 1 − 20○ = 5,47 мм

= − шаг для ИПК

= 12 = 37,699 мм

= ∑ – − коэффициент уравнительного смещения

= 0,4 − 0,368 = 0,032

21

= (2 − 2 ) − ширина впадины по делительной окружности

= − радиус основной окружности

= ( + 2 − ( − )) −толщина зубьев по дугам

2

окружностей вершин

= − углы профиля на окружностях вершин зубьев колёс

= 21 (1 − ) + 22 (2 − ) –коэффициент торцевого перекрытия (характеризует непрерывность и продолжительность зацепления).

Наличие скольжения профилей зубьев и давления одного профиля на другой при передаче сил приводит к износу. Коэффициент скольжения есть отношение скорости скольжения ск, и компоненты скорости точки контакта К по касательной к профилю соответствующего зубчатого колеса . Необходимо учитывать, что зубья большего зубчатого колеса входят в зацепление в 12 раз реже, чем зубья шестерни. Качество зубчатой передачи принято оценивать максимальными значениями коэффициентов скольжения в начале ( 1) и конце зацепления ( 2).

22

Коэффициент удельного давления учитывает влияние радиусов кривизны профилей зубьев на контактные напряжения. Расчётное значение коэффициента удельного давления принимают равным его значению в полюсе зацепления:

2(1 + 2)= 1 2

4.1.1. Станочное зацепление

Станочное зацепление представляет собой зацепление реечного исходного производящего контура с нарезаемым колесом. Эвольвентный профиль зуба колеса образуется как огибающая ряда положений исходного производящего контура реечного инструмента в станочном зацеплении. Такое образование профиля отражает реальный процесс изготовления колеса на станке. При этом эвольвентная часть профиля зуба образуется прямолинейной частью реечного инструмента производящего исходного контура, а переходная кривая профиля зуба - закругленным участком. При построении профиля зуба условно останавливают зубчатое колесо, а исходному производящему контуру, помимо поступательного движения, задают вращение со скоростью, обратной скорости зубчатого колеса. Таким образом, исходный производящий контур совершает плоское движение.

Построение:

1) Так как реечный инструмент - колесо бесконечного радиуса, то все окружности для него вырождаются в прямые. Проводим делительную прямую. На

23

расстоянии от делительной прямой проводим линии граничных точек. На расстоянии X1 m, с учетом знака (вниз - положительное направление), проводится станочно-начальная прямая. На расстоянии c m вверх от верхней линии граничных точек и вниз от нижней линии граничных точек проводятся линии вершин и впадин.

2)Из центра шестерни проводим окружности с радиусами 1 = 0, 1, 1, 1

3)Проводим горизонтальную линию касательно к окружности вершин шестерни. Отмечаем уравнительное смещение Δym и радиальный зазор C0.

4)Проводим линию касательно к основной окружности rb1 через точку P0 - линию станочного зацепления. Отмечаем точку касания N, угол станочного зацепления, равный углу профиля α=αw0. По делительной прямой от вертикальной оси откладываем влево отрезок равный:

= 20 = 4

Проводим через получившуюся точку линию, перпендикулярную линии зацепления. Отмечаем отрезок между линиями граничных точек вдоль этой прямой. Откладываем отрезок длины l влево еще раз. После этого симметрично отражаем построенный участок зуба рейки относительно вертикали. Проводим небольшие отрезки на линиях вершин и впадин, как на иллюстрации ниже. Проводим скругления . Копируем и симметрично отражаем элементы рейки для получения следующего результата.

5) Копируем выделенный профиль (см. рис.) режущего инструмента влево и вправо n раз через отрезок равный ΔS. Каждый профиль повернем относительно центра шестерни на угол Δφ i. Причем, профили,

которые расположены слева поворачиваются по часовой стрелке, а справа - против. Результатом поворота является множество огибающих к эвольвентному профилю.

Δφ = 1 − приращение угла

= 6 − число копий по каждую сторону от выделенного профиля

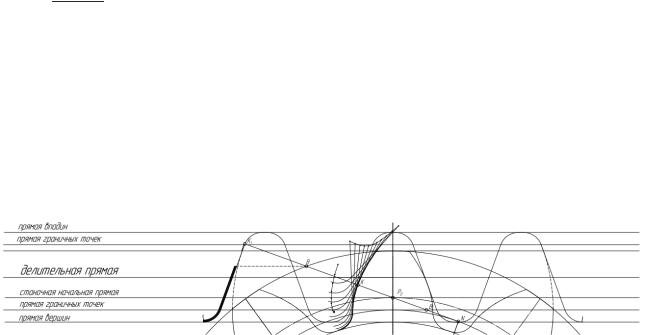
ΔS = 1180Δφπ ΔS = 6,28

6) Проводим огибающую ко всем построенным профилям. Используя инструмент радиусом проводим переходную кривую к окружности впадин rf. Проводим толщину зуба по окружности вершин. Отразив относительно вертикали получившуюся кривую, получаем профиль зуба, который копируем по окружности z1 раз.

4.1.2. Зубчатая передача

Данная зубчатая передача состоит из эвольвентных прямозубых цилиндрических колес с числами зубьев Z1=10, Z2= 20 и модулем, m = 12.

Построение:

1) Из центра шестерни проводим окружность 1 и откладываем аw. Из получившегося центра колеса проводим окружности с радиусами 2, 2,2, 2, 2. Проведем линию зацепления (касательная к основным окружностям). В точке касания построенной линии и основной окружности шестерни rb1

указываем точку N1, а в точке касания линии зацепления и основной окружности колеса rb2 указываем точку N2. Точки N1 и N2 ограничивают линию рабочего зацепления. В точке пересечения линии зацепления и линии, соединяющей центры шестерни и колеса, обозначаем точку P - полюс рабочего зацепления.

2)Соединяем точку P и N2 отрезком. Полученный отрезок разделяем на 7 равных частей. Делаем 3-4 копии отрезка с точкой ниже точки N2 по линии зацепления. Из точки N2 проводим окружности через поставленные точки. Ставим точки, в месте пересечения построенных окружностей с основной окружностью колеса. Замеряем длину отрезка lотр. Удаляем построенные окружности, отрезки и точки на линии зацепления. К точкам на основной окружности проводим отрезки из центра колеса. Из центра колеса проводим окружность произвольного радиуса, как на иллюстрации. Усекаем те части построенных отрезков, которые лежат ниже проведенной окружности. Перпендикулярно к оставшимся частям отрезков через точки на основной окружности колеса проводим отрезки длиной i lотр, где i - номер точки, начиная с 1. Проводим отрезки до тех пор, пока один из них не

25

пересечет окружность вершин колеса. Удаляем точки и отрезки, к которым не были построены перпендикуляры. Усекаем окружность. Поворачиваем относительно центра колеса элементы, которые были построены для нахождения эвольвентного профиля, в ту сторону, где построенный профиль не будет пересекаться с другими составляющими чертежа.

3)Соединяем концы отрезков эвольвентного профиля. Проводим отрезок, проходящий через точку пересечения эвольвентного профиля и окружности вершин колеса. Восстанавливаем к нему перпендикуляр, усекаем окружность и эвольвентный профиль. Поворачиваем профиль зуба относительно центра колеса так, чтобы зуб шестерни и колеса имели одну точку касания на линии зацепления. Симметрично отражаем профиль зуба относительно прямой, соединяющей центры шестерни и колеса. Проводим дугу по окружности вершин. Полученный профиль зуба копируем по окружности z2 раз.

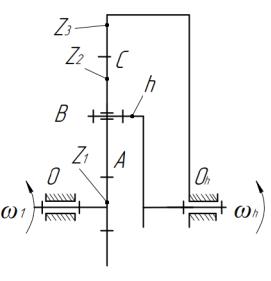
4.2. Проектирование планетарного зубчатого механизма

Исходные данные:

Однорядный планетарный редуктор с числом блоков сателлитов k=3 и передаточным отношением 1 = 5, = 0,8.

Схема редуктора:

При кинематическом синтезе планетарной зубчатой передачи, необходимо выполнить 7 условий:

1. Передаточное отношение проектируемого редуктора должно совпадать с заданным. Следует подчеркнуть, что это совпадение не обязательно должно быть абсолютным, допустимое отклонение передаточного отношения от заданного значения несколько процентов.

26

2. Второе условие, накладывает ограничение на выбор числа зубьев, связано с использованием в планетарном механизме зубчатых колес, нарезанных без смещения. Для исключения подрезания и заклинивания любого из колес с внешними зубьями внеш , нарезанных стандартным инструментом, принимают:

> = 17

а для колес с внутренними зубьями внутр

Во избежание интерференции зубьев при внутреннем зацеплении необходимо, чтобы разность чисел зубьев в зацеплении не была слишком маленькой. Обычно принимают:

внутр − внеш > 8

3. Соосное расположение центральных колес планетарного механизма с водилом. Условие соосности основных звеньев сводится к равенству межосевых расстояний входящих в зацепление колес сателлита с центральным колесом и с эпициклом.

В нашем случае все колеса имеют одинаковый модуль зацепления зубчатых колёс и это условие сводится к соотношению между числами зубьев:

1 + 2 = 3 − 2

4. Условие соседства, учитывает возможность свободного размещения сателлитов без их взаимного соприкосновения, будет выполнено, если расстояние между осями сателлитов превышает диаметр окружности вершин наибольшего сателлита.

2( 3) −число зубьев большего сателлита1 ± 2 −относительное межосевое расстояние между центральными колесами и сателлитом

1 + 2 −для внешнего зацепления; 1 − 2 −для внетреннего

5.Возможность свободного размещения сателлитов – условие сборки.

При симметрии зон зацепления это условие выражается соотношением:

1 1

где П=0,1,2,…- произвольное дополнительное число оборотов водила при сборке Ц – любое целое число

Подбор чисел зубьев:

31 = 1 + 1

1 + 2 = 3 − 2

1 > 17

27

2 > 203 > 58

1 = 18 => 3 = 1( 1 − 1)

Условие сборки:

1∙ 1 (1 + ∙ ) = -выполняется.

5 18 3 (1 + ∙ 3) = => 1 = 18

2 = 273 = 72

Условие соседства:

0,866>0,64 – выполняется. Из условия соосности:

1 + 2 = 3 − 2 => 18 + 27 = 72 − 27

45=45 – выполняется.

4.3. Проверка графическим способом правильности

передаточного отношения планетарного редуктора

Отметим точки А и С, в которых контактируют зубчатые колеса 1 и 2, 2 и 3. Эти точки лежат на оси симметрии ОС зубчатых колес. Отметит точку B в центре сателлита, которая является также точкой лежащей на оси водила h.

Зададимся отрезком АА’, изображающим скорость в точке А колеса 1. Так как колесо 1 вращается вокруг центра О, то закон распределения скоростей по колесу 1 изобразится линией ОА’.

Коронная шестерня неподвижная. Следовательно в точке С находится МЦС сателлита в абсолютном в абсолютном движении. В точке А сателлит имеет такую же скорость, что и колесо 1. Следовательно, закон распределения скоростей по сателлиту будет изображаться отрезком СА’.

Для определения скорости в точке В (центр сателлита) проведем из точки В линию ВВ’, параллельную АА’, до пересечения отрезком СA’. Так как точка В принадлежит также и оси пальца водила, а водило вращается вокруг оси О, то закон распределения скоростей по водилу изображается отрезком ОВ’, на котором поставим букву A’’.

28

1 ′1 = Н = ′′ = 5,005

5.Проектирование кулачкового механизма

5.1.Определение закона движения кулачкового механизма

Для решения данной задачи воспользуемся графическим методом интегрирования. Для определения передаточной функции скорости толкателя, используя метод Мерцалова, интегрируем заданную функцию ускорения толкателя, затем интегрируем полученную функцию скорости и находим функцию перемещения толкателя.

Масштаб угла поворота кулачка:

μ = 1 − масштаб по оси

b – выбранная база (мм)

1 − угол рабочего профиля кулачка

μ = – масштаб перемещений

- максимальная ордината на графике перемещений, мм

μ = μ 2 − масштаб аналога скорости толкателя, мм

μ

μ = μ 1 − масштаб аналога ускорения толкателя, мм

μ

5.2. Определение основных размеров кулачкового механизма

Основные размеры механизма определяют с помощью фазового портрета, представляющего собой зависимость ( ) . Фазовый портрет для механизма с поступательно движущимся толкателем строим методом графического исключения параметра 1 из диаграмм SB(1), VqB(1).

При построении фазового портрета используем μ = μ

Ограничим фазовый портрет лучами, ориентированными с учетом [ ]=30°, найдем центр О1, который находится в точке пересечения луча, отложенного под углом [ ]=30° от фазового портрета.

29

Из фазового портрета находим радиус центрового профиля: 0 = 0,14 м

Центровой профиль – профиль, по которому вращается центр ролика. Ролик введён в работу для снижения силы трения.

Радиус ролика: = (0,25 … 0,4) 0. Принимаем = 0,3 0 = 0,042 м

Если ≤ 0,25 0, то ролик будет слишком маленького размера, из чего следует:

Трудность подбора подшипника для данных размеров

Высокая скорость вращения ролика => большой износ

Если ≥ 0,4 0 может получиться заострение кулачка.

5.3. Построение профиля кулачка

При графическом построении профиля кулачка применяется метод обращения движения: звеньям механизма условно сообщают угловую скорость, равную − 1.

Построение:

Из центра вращения кулачка О1 строим окружность радиусом 0 с масштабом

μ = 2μ = 1087 мм/м

Точку О1 соединяют с произвольно выбранной точкой 0 на окружности радиуса r0. От луча 0 в направлении ω1 откладывается угол рабочего профиля кулачка 1. Дугу, соответствующую углу δраб, делят на части в соответствии с делением оси1 на графиках. Получаем точки 0,1,2… На прямых от точек 0,1,2,… откладываются отрезки SB в масштабе μ . Получаем точки 0’, 1’, 2’, ... и т.д. Соединяя полученные точки плавной кривой, получаем центровой (теоретический) профиль кулачка. Для получения конструктивного (рабочего) профиля кулачка строится эквидистантный профиль, отстоящий от центрового на величину радиуса ролика. Он получается как огибающая к дугам радиуса , проведенным из точек 0’, 1’, 2’, ... центрового профиля.

5.4. Построение графика изменения угла давления

По определению угол давления – угол между линией действия силы со стороны ведущего на ведомое звено со скоростью выходного (ведомого) звена => угол давления существует только на фазе удаления (когда кулачок толкает толкатель).

Проводим из точки О1 прямые, проходящие через точки 0-21 на графике фазового портрета. Измеряем угол между прямыми О10, О11, О12… и вертикалью.

Полученные углы откладываем на графике изменения угла давления, при этом выбрав масштабы:

мм

μ = 1,33 град

30