Итак,последовательностьрасчетавероятностиисправногосостояниясложногоизделия

1. Сформулироватьсловесноусловиеисправногосостоянияизделия.

2. Наосновелогическихопераций(дизъюнкция,конъюнкция,отрицание)записать

Fл.

3. ПреобразоватьвслучаенеобходимостиFл (минимизировать,исключить

повторяющиесячлены)

4. ПреобразоватьFлвFа.

5. Вфункции Fазаменитьпростыесобытияихвероятностями.

6. Вполученнуюформулу,устанавливающуюсвязьмеждувероятностямисостоянийэлементовисложногоизделия,подставитьчисленныезначениявероятностейсостоянийэлементов.

Аналогично, можно определить вероятность неисправного состояния сложного изделия,если рассматривать события, заключающееся в появлении отказа, т.е. неисправное состояниесистемы.

Использованиесистемы(5)предполагаетпоследовательно–параллельнуюструктуруобъектов.

Рассмотренный метод сводится к тому, чтобы исследуемый объект представить в видепоследовательно-параллельнойструктуры.

Частосоставлениятакойструктурырасчетанадежностиможноосуществитьнепосредственно либо по функциональной, либо принципиальнойсхеме объекта. При этомбудемиспользоватьследующиеправила.

1. Изобщегочислаэлементовсистемывыделимтакие,совместныйотказкоторыхприводиткотказусистемы.

Такиеэлементысоединимпараллельно.

2. Элементы,отказлюбогоизкоторыхприводиткотказусистемы,соединимпоследовательно.

При наличиипоследовательно-параллельныхструктурприрасчетенадежностиследуетпридерживатьсяопределеннойпоследовательностирасчета.

Нарис.4показанавозможнаяпоследовательностьрасчета.

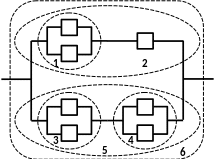5

Рис.4

Рассмотренные выше методы являются общими. Расчетные формулы для конкретныхслучаев расчета определяются в зависимости от вида использования объекта (свосстановлением, без восстановления), закона распределения, от характера резервирования,видарезервирования ит.д.

Расчетструктуртипа«звезда»и «треугольник»

Напрактикекромепоследовательно-параллельныхструктурвстречаютсяструктурытипа «треугольник» и «звезда», для которых необходимо найти эквивалентные уравненияисправности споследовательно-параллельной структурой.

₂ 2

Y

x

Z

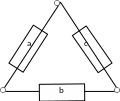₁ 3

Рис.1Треугольник

3

Рис.2 ЗвездаСоставимэквивалентныеуравненияисправностирассматриваемыхструктур.

т.1-2abc=xy

т.1-3bac=xzт.2-3cab=yz

(1)

гдеa,b,c,x,y,и z–события,заключающиесявисправномсостоянии.

Запишем систему (1) в арифметическом виде, подставив соответствующие вероятностисобытий.

^Pa^+Pb^Pc^{- P}a^Pb^Pc^=Px^Py^Pb^+Pa^Pc^{- P}b^Pa^Pc^=Px^Pz^Pc^+Pa^Pb^-Pc^Pa^Pb^=Py^Pz

(2)

^{Для случая P}a^=Pb^=Pc^{= P}т^{(для структурытреугольник)иP}x^=Py^=Pz^=Pз ^{(дляструктурызвезда)получим}

т т з

^Pт^{+P2- P3= P2 (3)}

Пример.

т т

Определить вероятность работоспособного состояния элемента звезда, полученную припреобразовании треугольника, если вероятность работоспособного состояния каждого^{элементатреугольникаравнаP}т =^0,9

^Pз^=Pт^+P2-P3=0,98

Рассмотримвкачествепримераструктурувида:

Рис.3

Преобразуем мостиковую схему (а-b-c) в схему типа звезда. Тогда получимпоследовательно-параллельнуюструктуру.

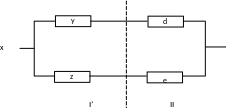
Рис.4

Определим в общем виде вероятность исправного состояния для данной схемы приусловии,чтовероятности исправногосостоянияэлементовa,b,c,dиeравныР=0,8.

P_З

Р_X

Р_Y

Р_Z

(4)

^Pз^=0,96

Для последней схемы (Рис.4) составим уравнение^P=PX^(Py^Pd^+Pz^Pe^-Py^Pd^Pz^Pe^{)=0,91 (5)P=0,91}