Элементы дифференциальной геометрии. Касательная и нормаль к плоской кривой.

Как было показано раньше, уравнение касательной к кривой в точке, которая называется точкой касания, имеет вид:

,

где

Определение. Прямая, проходящая через точку касания перпендикулярно к касательной, называется нормалью к кривой .

Используя условие перпендикулярности двух прямых, нетрудно вывести уравнение нормали:

или

.

Пример 1. Найти уравнение касательной и нормали к в точке.

Дифференцируя, получим и.

Уравнение касательной или,

т.к. .

Уравнение нормали

или

.

Пример 2. Касательная и нормаль к циклоиде:

Касательная и нормаль в точке будут иметь уравнения:

- касательная

- нормаль

Касательная и нормаль кривой, проведённые в , в пересечении сOX образуют . Катеты этого треугольника -и, отрезкии, на которые ординатаделит гипотенузу, часто используют в различных вопросах геометрии и получили специальные обозначения и названия:

- длина касательной,

- длина нормали,

- подкасательная,

- поднормаль.

Все эти отрезки лкгко могут быть вычислены через ив точке. В:

.

Поэтому:

или

Знаки модуля введены потому, что имогут быть меньше нуля.

Пример. Доказать, что - поднормальимеет для всех точек параболы одну и ту же длину.

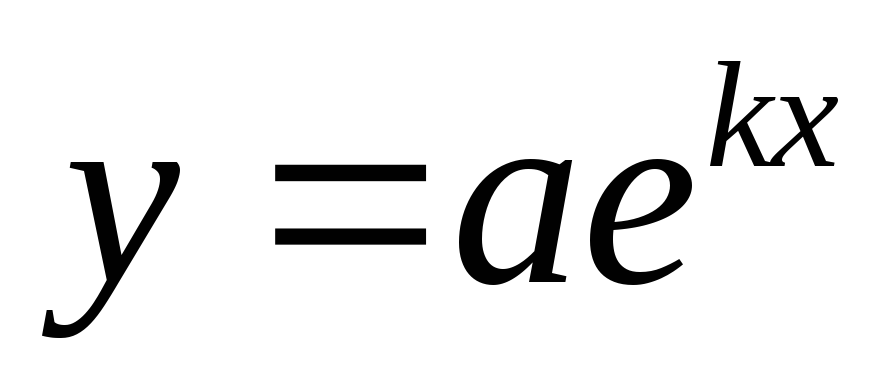2. имеет подкасательную - .

.

Дифференциал дуги плоской и пространственной кривой.

Определение. Кривые, для которых может быть установлено понятие длины, называются спрямляемыми.

Условие спрямляемости для плоской кривой, заданной заключается в следующем: на спрямляемом участке кривойидолжны иметь непрерывные производные поt - и. Аналогично записывается условие спрямляемости и пространственной кривой: непрерывность

Для всякой спрямляемой кривой справедливо геометрическое свойство: предел отношения б.м. дуги кривой к стягивающей её хорде равен 1, при условии, что хорда стягивается в точку. Если длину, а хорды -.

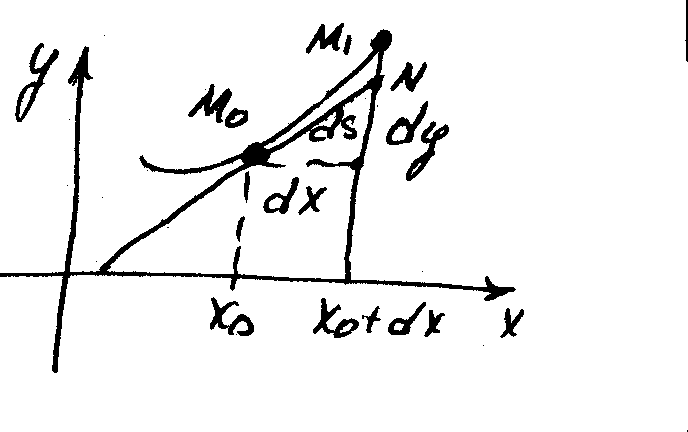
Опираясь на это свойство найдём выражение для дифференциала дуги кривой.

На плоской кривой возьмём 2 точкиикоторые соответствуюти. Длина хорды. Найдём теперь производную от длины дугипо:

,

т.к. при

и т.к.

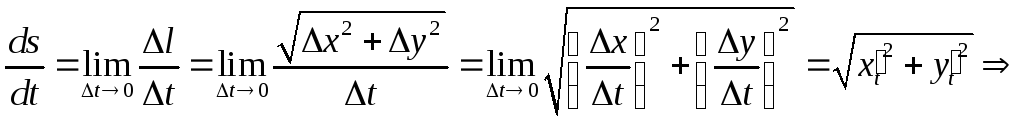
Если кривая задана , то принимаяза параметр кривой получим,и полагая в (*)получим

.

Если же кривая задана уравнением в полярных координатах , то за параметр можно принять угол, и тогда

.

Примеры. Найти для циклоиды.

Ответ:

Дифференциал дуги пространственной кривой находится аналогично. Отличие состоит в том, что длина хорды , соединяющейиопределяется формулой:

.

Пример. Винтовая линия:

Формулам для часто придают вид:

или ,

которые легко получить из предыдущих внося под знак корня и заменяя

.

Дифференциал дуги кривой имеет простой геометрический смысл: он равен длине отрезка касательной от точки касания до точки с абсциссой .

Кривизна плоской кривой.

Сравним между собой 2 кривые:и- имеющие в точкеодну и ту же касательную. Пустьи, лежащие наиимеют одну и ту же абсциссу. Очевидно, что более искривлённой является кривая, т.к. касательная к ней при переходе откповорачивается на больший угол. С другой стороны, при одинаковом угле поворота касательной более искривлена та дуга, длина которой меньше, т.е. кривая.

Т.о. можно принять, что мера кривизны конечного участка гладкой (дифференцируемой) кривой должна быть прямо пропорциональна углу, на который поворачивается касательная при переходе от начальной точки дуги к конечной и обратно пропорциональна длине этой дуги. Поэтому, за меру кривизны конечной дуги (средняя кривизна) можно принять отношение угла поворота касательной к длине дуги. Пусть - средняя кривизна,- угол смежности, на который поворачивается касательная при переходе отки- длина дуги. Тогда

.

Применим это определение к окружности радиуса . Для неёравен углу между радиусамии

.

Т.к. длина дуги .

Т.о. кривизна любой дуги окружности есть const.

Вывод естественный: любая дуга при перемещении её по окружности всеми точками будет лежать на окружности. При этом с уменьшением R кривизна будет возрастать.

Для кривых только для окружностии для прямой (0). Для других кривых, вероятно, кривизна – переменная величина. Она различна для дуг разной длины с общей точкой и зависит от положения на кривой.

Поэтому, естественно от понятия средней кривизны на данном участке перейти к понятию кривизны кривой в данной точке, совершая предельный переход при . За меру кривизны кривой в точке примем предел, к которому стремится средняя кривизна дуги, имеющей начало в заданной точке, когда длина.

.

Определение. Кривизна кривой в точке есть производная от угла поворота касательной к кривой по длине дуги. При этом угол поворота касательной можно измерять разностью углов касательных с осью, например, Х.

Выводим теперь формулу для вычисления кривизны кривой в любой её точке. Пусть- угол касательной сОХ. Тогда , а т.к.

.

Если не учитывать направление вогнутости кривой, то

.

Построим теперь окружность, которая имеет общую касательную с кривой в точке, общую кривизну и направление выгнутости. Такую окружность окружностью кривизны, её радиус – радиусом кривизны, а её центр – центром кривизны.

Т.к. кривизна окружности обратна её R, то для радиуса кривизны получим

(*) - радиус кривизны.

Центр кривизны лежит на нормали со стороны вогнутости кривой, на расстоянииот данной точки на кривой.

Рисунок соответствует случаю .

или

.

Но

(**) - координаты центра кривизны.

Т.к. иявляются функциями, то при изменении(как параметра) мы будем получать некоторую кривую, на которой лежат центры кривизны кривой.

Определение. Геометрическое место центров кривизны кривой называют её эволютой. Сама же криваяназывается эвольвентой по отношению к эволюте.

Пользуясь уравнениями (**) следующие свойства эволюты:

1. Касательная к эволюте в некоторой её точке служит соответствующая этой точке нормаль эвольвенты.

2. Дифференциал дуги эволюты равен дифференциалу радиуса кривизны эвольвенты.