Доказательство. Итак

Далее мы покажем, что эта формула верна и для * дробного и отрицательного.

Примеры: y=x⁵, y=

y=x, y=

Правила дифференцирования

1. Производная от y=x: y=x  y/x=1 

y=(x)=1

2. Производная от константы: y=c, y=0 для x , (c)=0

3. Производная суммы: y=u+v  y=u+v  

y=(u+v)=u+v

4. Производная произведения. y=uv  y+y=(u+u) (v+v) 

y=(u+u)(v+v)-uv=vu+uv+uv,здесь u и v не зависят от x.

 

y=(uv)=vu+uv, аналогично для любого числа сомножителей.

5. Постоянный множитель выносится за знак производной:

y=cu, y=(c)u+cu=cu  (cu)=cu

6. Производная частного .

, 

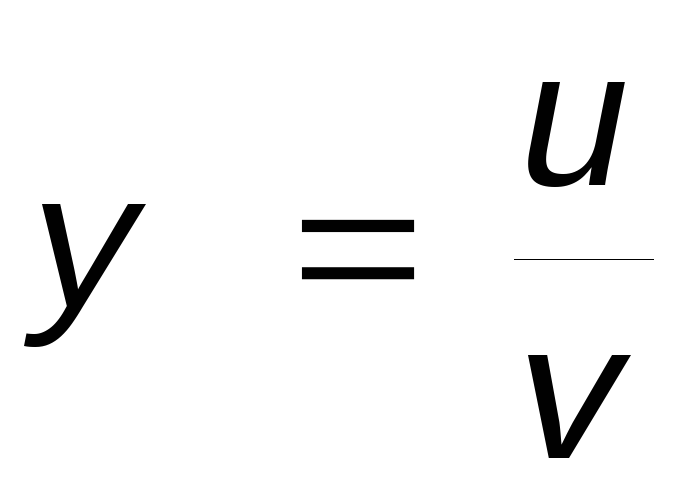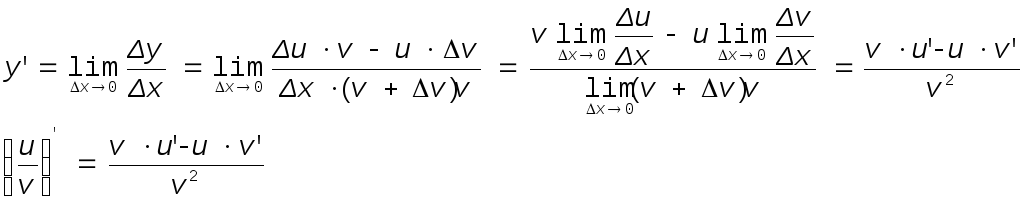
7. Правило дифференцирования обратной функции.

Как известно, для монотонной на (a,b) y=f(x) существует однозначная обратная функция x=(y). Если f(x) дифференцируема, то при всех x, при которых f(x)0, (y) также дифференцируема, причем

или или .

Эта формула следует из того факта, что :

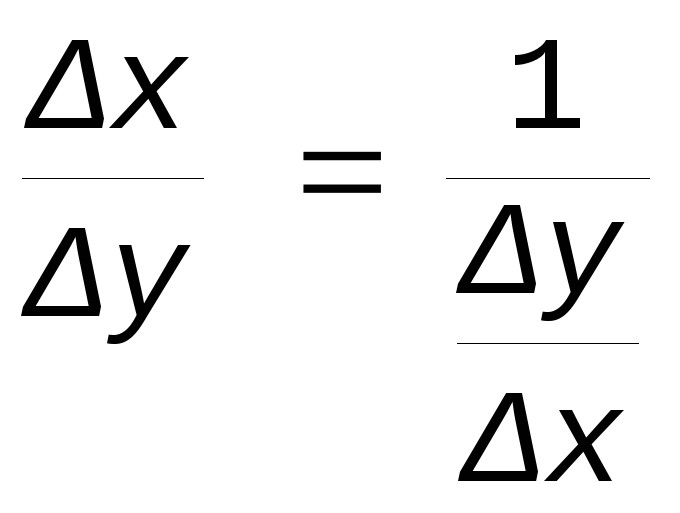
и того, что x и y 0 одновременно, причем x0 и y0 в силу монотонности. Поэтому

Геометрический смысл.

Обе функции прямая – y=f(x) и обратная – x=(y) имеют один и тот же график.

y_x=f(x) есть tg,где  - угол, образованный касательной с осью ОХ (касательная в точке (x,y)).

y_x= tg

Аналогично: x_y= tg, где  - угол, образованный той же касательной в той же точке (x,y), но с осью ОУ. Так как +=/2 

tg=1/tg или tg=1/tg.

или

8. Правило дифференцирования сложной функции.

Пусть y=f(z) и z=(x) - дифференцируемые функции своих аргументов.

Тогда в некоторой области x’, y будет сложной функцией от x  y=f((x)).

Докажем, что y_x=(f((x)))=y_zz_x.

Теорема. Производная от сложной функции y по независимому аргументу x равна производной от y по промежуточному аргументу z, умноженной на его (z) производную по аргументу x.

Доказательство. В силу дифференцируемости y=f(z) по z имеем

 y=(y_z+)z, где  - бесконечно малая, z0, то есть

.

Аналогично z=(z_x+)x, где 

.

Эта теорема справедлива для любого конечного числа суперпозиций функциональных зависимостей. Например:

y=f(z), z=(u), u=(v), v=(x) 

yx=f_zz_uu_vv_x.

Все приведенные правила дифференцирования (и особенно последнее) имеют первостепенное значение, так как позволяют находить производные, образованные от любых элементарных функций, образованных при помощи алгебраических действий и наложения функциональных зависимостей. Конечно при условии, что производные основных элементарных функций уже нам известны.

Производные от основных элементарных функций.

1. Показательная функция y=a^x.

x  y=a^x+x-a^x=a^x(a^x-1)



y=(a^x)= a^xlna  a=e  (e^x)= e^x

2. Логарифмическая функция y=log_ax.

Здесь сразу можно использовать правило логарифмического обр. функции x=a^y  и тогда x_y=a^ylna=xlna, и тогда

т.к.

При a=e имеем

.

3. Степенная функция y=xⁿ, где nR, x>0.

Полагая x=e^lnx получим y=e^nlnx, будем дифференцировать ее как сложную функцию.

4. Функции y=sin x и y=cos x

y=sin(x+x)-sin x=2sinx/2cos(x+x/2)

(sin x)=cos x

Так как cos x=sin(x+/2)  полагая y=sin z, z=x+/2 

y = (cos x) = (sin z)_zz_x = cos z = cos (x+/2) = -sin x.

y = (cos x) = -sin x.

5. tg x и ctg x.

6. Функции y=arcsin x и y=arccos x

а) Так как y=sin x  x_y= cos x=1-sin²y=1-x² ,

+, т.к. и cos y0 

б) arcsin x + arccos x = /2 

arccos x = /2 - arcsin x

7. y= arctg x и y=arcctg x

а) x=tg y, x_y = sec²y = 1+tg²y = 1+x²

б) Аналогично arctg x + arcctg x = /2 и

Сводка