SGK_drive / Class 11 / 301_20201026023852_dai-so---da-ghep

(T¸i b¶n lÇn thø b¶y) 11

Nhµ xuÊt b¶n gi¸o dôc viÖt nam

KÝ hiÖu dïng trong s¸ch

PhÇn ho¹t ®éng cña häc sinh.

Tuú ®èi t−îng cô thÓ mµ gi¸o viªn sö dông.

KÕt thóc chøng minh hoÆc lêi gi¶i.

B¶n quyÒn thuéc Nhµ xuÊt b¶n Gi¸o dôc ViÖt Nam − Bé Gi¸o dôc vµ §µo t¹o.

01 − 2014/CXB/472 − 1062/GD M· sè : CH101T4

hμm sè l−îng gi¸c

I − ®Þnh nghÜa

Tr−íc hÕt, ta nh¾c l¹i b¶ng c¸c gi¸ trÞ l−îng gi¸c cña c¸c cung ®Æc biÖt.

1

a)Sö dông m¸y tÝnh bá tói, h·y tÝnh sin x, cos x víi x lµ c¸c sè sau :

π; π ; 1,5 ; 2 ; 3,1 ; 4,25 ; 5.

64

b)Trªn ®−êng trßn l−îng gi¸c, víi ®iÓm gèc A, h·y x¸c ®Þnh c¸c ®iÓm M mµ sè ®o cña

cung AM b»ng x (rad) t−¬ng øng ®· cho ë trªn vµ x¸c ®Þnh sin x, cos x (lÊy π ≈ 3,14).

1. Hµm sè sin vµ hµm sè c«sin

a) Hµm sè sin

ë líp 10 ta ®· biÕt, cã thÓ ®Æt t−¬ng øng mçi sè thùc x víi mét ®iÓm M duy

nhÊt trªn ®−êng trßn l−îng gi¸c mµ sè ®o cña cung AM b»ng x (rad) (h.1a). §iÓm M cã tung ®é hoµn toµn x¸c ®Þnh, ®ã chÝnh lµ gi¸ trÞ sin x.

4

BiÓu diÔn gi¸ trÞ cña x trªn trôc hoµnh vµ gi¸ trÞ cña sin x trªn trôc tung, ta ®−îc H×nh 1b.

H×nh 1

Quy t¾c ®Æt t−¬ng øng mçi sè thùc x víi sè thùc sin x sin : \ → \

x y = sin x

®−îc gäi lµ hµm sè sin, kÝ hiÖu lµ y = sin x. TËp x¸c ®Þnh cña hµm sè sin lµ \.

b) Hµm sè c«sin

TËp x¸c ®Þnh cña hµm sè c«sin lµ \.

5

2.Hµm sè tang vµ hµm sè c«tang

a)Hµm sè tang

Hµm sè tang lµ hµm sè ®−îc x¸c ®Þnh bëi c«ng thøc

V× cos x ≠ 0 khi vµ chØ khi x ≠ π + kπ (k ]) nªn tËp x¸c ®Þnh cña hµm 2

sè y = tan x lµ

D = \ \ {π2 + kπ, k Z}.

b) Hµm sè c«tang

Hµm sè c«tang lµ hµm sè ®−îc x¸c ®Þnh bëi c«ng thøc

= cos x

y

sin x

kÝ hiÖu lµ y = cot x.

V× sin x ≠ 0 khi vµ chØ khi x ≠ kπ (k ])

y = cot x lµ

D = \ \ {kπ, k

2

H·y so s¸nh c¸c gi¸ trÞ sin x vµ sin (−x), cos x vµ

NhËn xÐt

Hµm sè y = sin x lµ hµm sè lÎ, hµm sè y = cos x lµ hµm sè ch½n, tõ ®ã suy ra c¸c hµm sè y = tan x vµ y = cot x ®Òu lµ nh÷ng hµm sè lÎ.

II − TÝnh tuÇn hoµn cña hµm sè l−îng gi¸c

3

T×m nh÷ng sè T sao cho f(x + T) = f(x) víi mäi x thuéc tËp x¸c ®Þnh cña c¸c hµm sè sau : a) f(x) = sin x ; b) f(x) = tan x.

6

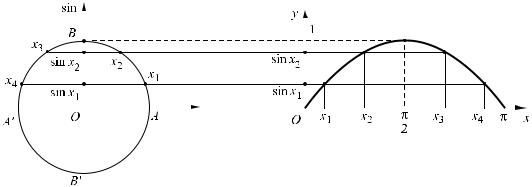
Ng−êi ta chøng minh ®−îc r»ng T = 2π lµ sè d−¬ng nhá nhÊt tho¶ m·n ®¼ng thøc

sin(x + T) = sin x, x \ (xem Bµi ®äc thªm).

Hµm sè y = sin x tho¶ m·n ®¼ng thøc trªn ®−îc gäi lµ hµm sè tuÇn hoµn víi chu k× 2π.

T−¬ng tù, hµm sè y = cos x lµ hµm sè tuÇn hoµn víi chu k× 2π.

C¸c hµm sè y = tan x vµ y = cot x còng lµ nh÷ng hµm sè tuÇn hoµn, víi chu k× π.

III − Sù biÕn thiªn vµ ®å thÞ cña hµm sè l−îng gi¸c

1. Hµm sè y = sin x

Tõ ®Þnh nghÜa ta thÊy hµm sè y = sin x :

y X¸c ®Þnh víi mäi x \ vµ −1 ≤ sin x ≤ 1 ;

yLµ hµm sè lÎ ;

yLµ hµm sè tuÇn hoµn víi chu k× 2π.

Sau ®©y, ta sÏ kh¶o s¸t sù biÕn thiªn cña hµm sè y = sin x.

a) Sù biÕn thiªn vµ ®å thÞ hµm sè y = sinx trªn ®o¹n [0 ; π]

BiÓu diÔn chóng trªn ®−êng trßn l−îng gi¸c vµ xÐt sin xi t−¬ng øng (i = 1, 2, 3, 4) (h.3a).

§å thÞ cña hµm sè y = sin x trªn ®o¹n [0 ; π] ®i qua c¸c ®iÓm (0 ; 0), (x1 ; sin x1), (x2 ; sin x2), π2 ; 1 , (x3 ; sin x3), (x4 ; sin x4), (π ; 0) (h.3b).

Chó ý

V× y = sin x lµ hµm sè lÎ nªn lÊy ®èi xøng ®å thÞ hµm sè trªn

®o¹n [0 ; π] qua gèc to¹ ®é O, ta ®−îc ®å thÞ hµm sè trªn ®o¹n [−π ; 0].

§å thÞ hµm sè y = sin x trªn ®o¹n [−π ; π] ®−îc biÓu diÔn trªn H×nh 4.

H×nh 4

b) §å thÞ hµm sè y = sin x trªn \

Hµm sè y = sin x lµ hµm sè tuÇn hoµn chu k× 2π nªn víi mäi x \ ta cã sin(x + k2π) = sin x, k ].

Do ®ã, muèn cã ®å thÞ hµm sè y = sin x trªn toµn bé tËp x¸c ®Þnh \, ta tÞnh tiÕn liªn tiÕp ®å thÞ hµm sè trªn ®o¹n [−π ; π] theo c¸c vect¬ vG = (2π ; 0) vµ −vG = (−2π ; 0) , nghÜa lµ tÞnh tiÕn song song víi trôc hoµnh tõng ®o¹n cã ®é dµi 2π.

8

H×nh 5 d−íi ®©y lµ ®å thÞ hµm sè y = sin x trªn \.

Ta nãi tËp gi¸ trÞ cña hµm sè nµy lµ [−1 ; 1].

2. Hµm sè y = cos x

Tõ ®Þnh nghÜa ta thÊy hµm sè y = cos x :

y X¸c ®Þnh víi mäi x \ vµ −1 ≤ cos x ≤ 1 ;

yLµ hµm sè ch½n ;

yLµ hµm sè tuÇn hoµn víi chu k× 2π. Víi mäi x \ ta cã ®¼ng thøc

thÞ cña hµm sè y = cos x (h.6).

H×nh 6

9