

BO GIAO Dgc VA DAO TAO
TRAN VAN HAG (Tong ChCi bien)
NGUYEN M'ONG HY (ChCi bien)
KHU QUOC ANH - NGUYI'N HA THANH - PHAN VAN VIEN
HINH HOC
11
(Tdi bdn ldn thti ba)
NHA XUAT BAN GIAO DUG VIET NAM

Kl hieu dung trong sach
Hoqt dong cGo hqc sinh tren I6p
Ban quy6n thupc Nha xua't ban Giao due Viet Nam - B6 Giao due va Dao tao.
01-2010/CXB/567-1485/GD |
Masd:CH102TO |
CHCdNG
PHEP Ddi HiNH
VA PHEP odiSIG DANG
TRONG M A T PHANG
I 111 I I |
I I I , |
I |
I I I |
1,1 |
I |
*> Phep tjnh tien, phep do! xumg true, phep doi xumg tam va phep quay
*> Khai niem ve phep ddi hinh va hai hinh b^ng nhau *> Phep vj tir, tam vj tircua hai dudng trdn
*> Khai niem ve phep dong dang va hai hinh dong dang
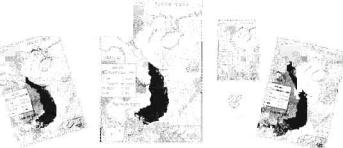
Nhin nhumg tam ban do Viet Nam tren day ta th% do la nliung liinh giong nhau cCing nam tren mot mat phlng.
Hai hinli tji^ va S> giong nhau c& ve hinh dang va l^icli
thi/dc, chung chi l<hac nhau ve vj tri tren mat phlng. Hai
hinh . ^va "^giong nhau ve hinh dang nhi/ng khae nhau
ve l<ich thude va vj tri. Ta goi t.js^ va S> la hai hinh bang
nhau, con ^ v a '^la hai hinh dong dang vdi nhau. Vay
the nao la hai hinh bang nhau hay dong dang v6i nhau ? Trong chtfong nay ta se nghien cufu ve nhiJng van de do.
§1. PHEP BIEN HINH
^ 1 Trong mat phang cho dudng thing d va 6\im M. Dung hinh chi^u vudng gde M' cija didm M len dudng thing d.
Ta da bi6't rang vdi mdi didm M co mdt |
M |
|
|
||
dilm M' duy nhSit la hinh chi6u vudng gde |
|
|
cua dilm M irtn dudng thing d chd tnrdc |
|
|
(h.1.1). |
|
|
Tacd dinh nghia sau. |
^ ' |
|
/ |
Hinh 1.1 |
|
I Dinh nghla |
||
|
Quy tdc ddt tuang Ang mdi diem M cua mat phang vdi mgt diem xdc dinh duy nhdt M' cua mat phdng do duac goi la phep bien hinh trong mat phdng.
Ne'u kl hieu phep bie'n hinh la F thi ta vie't F{M) = M' hay M' = F{M) va goi dilm M' la anh ciia dilm M qua phep bi^'n hinh F.
«
Ne'u <30 la mdt hinh nao dd trong mat phang thi ta ki hieu t3^' = F{o^) la tap
cac dilm M' = F{M), vol moi diem M thude J ^ . Khi dd ta ndi F bien hinh ^ thdnh hinh ^', hay hinh ^ ' Id dnh ciia hinh e^i^qua phep bieh hinh F.
Phep bie'n hinh bie'n mdi dilm M thanh chfnh nd duoc goi la phep dong nhdt.
^ 2 Cho trudc sd a duong, vdi mdi didm M trong mat phang, gpi M ' la didm sao cho MM' = a. Quy tac dat tuong urng didm M vdi 6\im M' n6u tr6n cd phai |a mdt phep biS'n hinh Ichdng ?
§2. PHEP TjNH TIEN
Khi day mdt canh cufa tnrcrt sao cho chdt cura |
|
|
|
dich chuyin tit vi tri A de'n vi tri B ta tha'y tijtng |
|
|
|
dilm cua canh cira cung duoc dich ehuyin |
AS |
^ B |
|
mdt doan bang AB va theo hudng ttt A den B |
|||
|
|
||
(h.1.2). Khi dd ta ndi canh cijfa duoc tinh tie'n |
|
|
|
theo vectd AB. |
|
|
Hint) 1.2
I. DINH NGHIA
Djnh nghia
'§ Trong mat phdng cho vecta v. Phep bien hinh bien mdi diem
M thdnh diem M' sao cho MM' = v duac gpi la phep tinh tien theo vecta v (h.l.3).
Phip tinh tie'n theo vecto v thudng duoc ki hieu la r^, V duoc goi la vecta tinh tien.
Nhu vay
T^{M)=M'<^ MM' = v.
Phip tinh tie'n theo vecto - khdng chinh Ihphep ddng nhdt.
Vidu
a)Phep tinh tie'n T^ bigh cac dilm A, B, C tuong ling thanh cac dilm A', B', C
(h.l.4a).
b) Phep tinh tie'n T- bie'n hinh J ^ thanh hinh J ^ ' (h.l.4b).
|
A |
|
. |
^• |
-' '/ \ |
'^N |
|
/ |
|
||
A ^-- '' |
/ |
N |
c |
^'" B |
^,' |
||
^^-• • '
^ * |
^-^"* |
-» |
|
B |
c |
|
|
' |
|
|
|
|
a) |
|
b) |
|
|
HOT/7 |
1.4 |
1 Cho hai tam gi^c d§u ABE va BCD bang nhau tr§n hinh 1.5. Tim pli§p tinh ti^n bien ba diem A, B, E theo thur ty thanh ba di^m B, C, D.
Hinh 1.5

Hinh 1.7
2 N§u cSch xSc dinh iinh cCia dudng thing d qua ph6p tmh ti^n theo vecto v .
y\
ra. BI^U THtfC TOA D O
Trong mat phing toa dd Oxy cho vecto v= (a ; 6) (h.'l.8). Vdi mdi dilm M{x ; y) ta ed M'{x' ; y") la anh c6a M qua ph6p tinh ti^n theo
vecto |
V. Khi |
dd |
MM' = v <=> |
|
{x'-x |
= a ^^ |
^^ |
[x' = x + a |
|
\ , |
Tit dd suy ra ^ |
, |
||
[y-y |
= b. |
|
\y |
=y+b. |
Hinh 1.8
Bilu thiic tren dugc ggi 1^ bi/u thiic tog dd eiia phip tinh ti6i T-.
3Trong mat phlng tea dd Oxy cho vecto v = ( 1 ; 2). Tim tea dd cOa didm M' Id inh cOa dilm M{3 ; -1) qua ph6p tjnh ti^n T^.
BAITAP
1. Chiing minh rang : M' = T- {M)^M = r_- (M').
2.Cho tam gific ABC cd G la trgng tam. Xdc dinh anh eua tam gidc ABC qua phip tinh tieh theo vecto AG. XAc dinh dilm D sao cho phep tinh ti^n theo' vecto AG bie'n D thanh A.
3.Trong mat phang tda dd Oxy cho vecto v = (-1 ; 2), hai dilni A{3 ; 5), 5(-l ; 1) va dudng thang d cd phuang trinh jc - 2>' + 3 = 0.
a)Tim toa dd cua cdc dilm A',B' theo thu: tu la anh eua A, B qua phep tinh tie'n theo V.
b)Tim toa dd cua dilm C sao cho A la anh ciia C qua phep tinh tie'n theo v.
c)Tim phirong tnnh eua dudng thang d' la anh eiia d qua phep tinh ti6i theo v.

