525_20200918030407_dai-so---nc---da-ghep

Добавил:

maiminh06 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

. Ng−êi ta th−êng kÝ

®óng mét nghiÖm n»m trong kho¶ng

hiÖu nghiÖm ®ã lµ arctan m (®äc lµ ¸c-tang m). Khi ®ã

tan x = m x = arctan m + k .

.pdf

Скачиваний:

Добавлен:

01.01.2023

Размер:

5.8 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 253 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

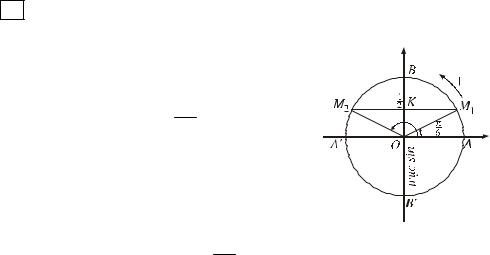
H1 T×m mét nghiÖm cña ph−¬ng tr×nh (1).

§Ó t×m tÊt c¶ c¸c nghiÖm cña (1), ta cã thÓ

lµm nh− sau :

XÐt ®−êng trßn l−îng gi¸c gèc A. Trªn trôc sin, ta lÊy ®iÓm K sao cho OK = 12 . §−êng

th¼ng qua K vµ vu«ng gãc víi trôc sin c¾t ®−êng trßn l−îng gi¸c t¹i hai ®iÓm M1 vµ M2 ; hai ®iÓm nµy ®èi xøng víi nhau qua trôc sin

(h. 1.19). Ta cã

H×nh 1.19

sin(OA, OM1) = sin(OA, OM2) = OK = 12

DÔ thÊy, sè ®o (ra®ian) cña c¸c gãc l−îng gi¸c (OA, OM1) vµ (OA, OM2) lµ tÊt c¶ c¸c nghiÖm cña (1). LÊy mét nghiÖm tuú ý cña (1), ch¼ng h¹n x 6 . Khi ®ã

c¸c gãc (OA, OM1) cã sè ®o 6 k2 ; c¸c gãc (OA, OM2) cã sè ®o

k2 (k ). VËy

sin x = 21 x =

6 + k2 hoÆc x =

6 + k2 (k ).

Sö dông kÝ hiÖu "[" thay cho tõ "hoÆc", ta cã thÓ viÕt l¹i kÕt qu¶ trªn nh− sau :


1	x	6	k2
sin x = 2					(k ).
					k2
	x			6	k2
				6
b) Gi¶ sö m lµ mét sè ®· cho. XÐt ph−¬ng tr×nh
sin x = m.					(I)

HiÓn nhiªn ph−¬ng tr×nh (I) x¸c ®Þnh víi mäi x .

Ta ®· biÕt, sin x 1 víi mäi x. Do ®ã ph−¬ng tr×nh (I) v« nghiÖm khi m > 1. MÆt kh¸c, khi x thay ®æi, sin x nhËn mäi gi¸ trÞ tõ 1 ®Õn 1 nªn ph−¬ng tr×nh (I) lu«n cã nghiÖm khi m 1.

Lµm t−¬ng tù nh− ®èi víi ph−¬ng tr×nh (1), ta cã

NÕu lµ mét nghiÖm cña ph−¬ng tr×nh (I), nghÜa lµ sin = m th×

sin x = m	x k2	(k ).	(Ia)
	x k2

Ta nãi r»ng x = + k2 vµ x = + k2 lµ hai hä nghiÖm cña ph−¬ng tr×nh (I).

KÓ tõ ®©y, ®Ó cho gän ta quy −íc r»ng nÕu trong mét biÓu thøc nghiÖm cña ph−¬ng tr×nh l−îng gi¸c cã chøa k mµ kh«ng gi¶i thÝch g× thªm th× ta hiÓu

r»ng k nhËn mäi gi¸ trÞ thuéc . Ch¼ng h¹n, x = + k2 cã nghÜa lµ x lÊy mäi gi¸ trÞ thuéc tËp hîp

{ , 2 , 4 , 6 , ...}. VÝ dô 1. Gi¶i c¸c ph−¬ng tr×nh sau :

1) sin x =		3	;				2)	sin x =	2
1) sin x =		2	;				2)	sin x =	3
		2							3
Gi¶i
				3
1) Do sin					nªn
1) Do sin					nªn
		3		2

	3							x	3	k2
sin x =		sin x sin
sin x =		sin x sin
	2					3
								x			3	k2

x k2 ,x 4 3 k2 .

2) V× 23 < 1 nªn cã sè ®Ó sin = 23 . Do ®ã

sin x =	2	sin x = sin	x k2 ,	
	3		x k2 .

		2
H2	Gi¶i ph−¬ng tr×nh sin x
		2

Trong mÆt ph¼ng to¹ ®é, nÕu vÏ ®å thÞ (G ) cña hµm sè y = sin x vµ ®−êng

th¼ng (d ) : y = m th× hoµnh ®é mçi giao ®iÓm cña (d ) vµ (G ) (nÕu cã) lµ mét nghiÖm cña ph−¬ng tr×nh sin x = m.

H3 Trªn ®å thÞ hμm sè y = sin x (h.1.20), h·y chØ ra c¸c ®iÓm cã hoμnh ®é trong

	kho¶ng (0 ; 5 ) lμ nghiÖm cña ph−¬ng tr×nh sin x =																						2
	kho¶ng (0 ; 5 ) lμ nghiÖm cña ph−¬ng tr×nh sin x =																						2
																							2

H×nh 1.20
Chó ý
1) Khi m {0 ; 1}, c«ng thøc (Ia) cã thÓ viÕt gän nh− sau :
sin x = 1	x		k2 ,
		2	k2 ,
sin x = 1	x		k2 ,
			2
sin x = 0	x = k .
2) DÔ thÊy r»ng víi	m cho	tr−íc mµ		m	1, ph−¬ng tr×nh
2) DÔ thÊy r»ng víi	m cho	tr−íc mµ		m	1, ph−¬ng tr×nh

sin x m	cã ®óng mét nghiÖm n»m trong ®o¹n		;			Ng−êi
		2		2	.

ta th−êng kÝ hiÖu nghiÖm ®ã lµ arcsin m (®äc lµ ¸c-sin m). Khi ®ã

sin x m	x arcsin m k2 ,
sin x m
	x arcsin m k2 .
VËy ë vÝ dô 1 c©u 2) cã thÓ viÕt
			2	k		2 ,
	2	x arcsin		k		2 ,
sin x			3
sin x	3				2
	3				2	k2 .
		x arcsin			3	k2 .
					3

3) Tõ (Ia) ta thÊy r»ng : NÕu vµ lµ hai sè thùc th× sin sin
khi vµ chØ khi cã sè nguyªn k	®Ó		k2 hoÆc
k2 , k .
VÝ dô 2. T×m sè x tho¶ m·n ph−¬ng tr×nh sin(2x
VÝ dô 2. T×m sè x tho¶ m·n ph−¬ng tr×nh sin(2x		) sin		x .
	5		5

Gi¶i

									x k2
						2x	5	5	x k2
	2x						5	5
sin	2x	5	sin	5	x
		5		5
						2x	5			5	x	k2

		x		2						2
					k2		x						k2
										5			k2
										5
			5											2
														2
		3x k2										k
		3x k2					x		3			k		3
									3					3
VËy c¸c sè x cÇn t×m lµ	x	2	k2 vµ x				k	2			, k .				
VËy c¸c sè x cÇn t×m lµ	x	5	k2 vµ x			3	k		3		, k .				

H4 Gi¶i ph−¬ng tr×nh sin 2x sin x .

2.Ph−¬ng tr×nh cosx = m

XÐt ph−¬ng tr×nh

cos x = m, (II)

trong ®ã m lµ mét sè cho tr−íc. HiÓn nhiªn ph−¬ng tr×nh (II) x¸c ®Þnh víi mäi x . DÔ thÊy r»ng :

Khi m > 1, ph−¬ng tr×nh (II) v« nghiÖm.

Khi m 1, ph−¬ng tr×nh (II) lu«n cã nghiÖm. §Ó t×m tÊt c¶ c¸c nghiÖm cña (II),

trªn trôc c«sin ta lÊy ®iÓm H sao cho OH = m. Gäi (l ) lµ ®−êng th¼ng ®i qua H vµ vu«ng gãc

víi trôc c«sin (h. 1.21).

H×nh 1.21

Do m 1 nªn ®−êng th¼ng (l ) c¾t ®−êng trßn l−îng gi¸c t¹i hai ®iÓm M1 vµ M2. Hai ®iÓm nµy ®èi xøng víi nhau qua trôc c«sin (chóng trïng nhau nÕu m = 1). Ta thÊy sè ®o cña c¸c gãc l−îng gi¸c (OA, OM1) vµ (OA, OM2) lµ tÊt c¶ c¸c nghiÖm cña (II). NÕu lµ sè ®o cña mét gãc trong chóng, nãi c¸ch kh¸c, nÕu lµ mét nghiÖm cña (II) th× c¸c gãc ®ã cã c¸c sè ®o lµ+ k2 vµ + k2 . VËy ta cã

		NÕu lµ mét nghiÖm cña ph−¬ng tr×nh (II), nghÜa lµ cos = m th×
		x k2 ,				(IIa)
		cos x = m	k2 .			(IIa)
		x	k2 .
				2	.
H5	Gi¶i ph−¬ng tr×nh sau : cos x =			2
H5	Gi¶i ph−¬ng tr×nh sau : cos x =		2
		Chó ý	2
		Chó ý
		1) §Æc biÖt, khi m {0 ;		1}, c«ng thøc (IIa) cã thÓ viÕt gän
		nh− sau
		cos x = 1			x = k2 ,
		cos x = 1 x = + k2 ,
		cos x = 0			x =	+ k .
						2

2) DÔ thÊy r»ng víi mäi sè m cho tr−íc mµ m 1, ph−¬ng tr×nh cos x = m cã ®óng mét nghiÖm n»m trong ®o¹n [0 ; ]. Ng−êi ta th−êng kÝ hiÖu nghiÖm ®ã lµ arccos m (®äc lµ ¸c-c«sin m). Khi ®ã

x arccos m k2 , cos x = m

x arccos m k2 . mµ còng th−êng ®−îc viÕt lµ x = arccos m + k2 .

3) Tõ (IIa) ta thÊy r»ng : NÕu vµ lµ hai sè thùc th× cos cos khi vµ chØ khi cã sè nguyªn k ®Ó k2 hoÆc k2 , k .

H6 H·y gi¶i ph−¬ng tr×nh cos(2x 1) cos(2x 1) .

3. Ph−¬ng tr×nh tan x = m

Cho m lµ mét sè tuú ý. XÐt ph−¬ng tr×nh

tan x = m.	(III)
§iÒu kiÖn x¸c ®Þnh (§KX§) cña ph−¬ng
tr×nh (III) lµ cos x 0.

Ta ®· biÕt, khi x thay ®æi, tan x nhËn mäi gi¸ trÞ tõ ®Õn + . Do ®ã ph−¬ng tr×nh (III) lu«n cã nghiÖm. §Ó t×m tÊt c¶ c¸c nghiÖm cña (III), trªn trôc tang, ta lÊy

®iÓm T sao cho AT = m. §−êng th¼ng OT c¾t ®−êng trßn l−îng gi¸c t¹i hai ®iÓm M1

vµ M2 (h. 1.22). Ta cã			H×nh 1.22
tan(OA, OM1) = tan(OA, OM2) = AT = m.

Gäi sè ®o cña mét trong c¸c gãc l−îng gi¸c (OA, OM1) vµ (OA, OM2) lµ ; nãi c¸ch kh¸c, lµ mét nghiÖm nµo ®ã cña ph−¬ng tr×nh (III). Khi ®ã, c¸c

gãc l−îng gi¸c (OA, OM1) vµ (OA, OM2) cã c¸c sè ®o lµ + k . §ã lµ tÊt c¶ c¸c nghiÖm cña ph−¬ng tr×nh (III) (hiÓn nhiªn chóng tho¶ m·n §KX§ cña (III)). VËy ta cã

NÕu lµ mét nghiÖm cña ph−¬ng tr×nh (III), nghÜa lµ tan = m th× tan x = m x = + k . (IIIa)

VÝ dô 3. Gi¶i c¸c ph−¬ng tr×nh sau :
1)	tan x = 1 ;		2) tan	x	3 .
1)	tan x = 1 ;		2) tan		3 .
			3
Gi¶i
1)	V× 1 = tan		nªn
1)	V× 1 = tan		nªn
		4

tan x = 1 x = 4 + k .

2) Gäi lµ mét sè mµ tan = 3. Khi ®ã

tan 3x 3 3x k x 3 k3 .

(Cã thÓ t×m ®−îc mét sè tho¶ m·n tan = 3 b»ng c¸ch tra b¶ng sè hoÆc dïng m¸y tÝnh bá tói. Cô thÓ lµ 1,249). 

Chó ý

1) DÔ thÊy r»ng víi mäi sè m cho tr−íc, ph−¬ng tr×nh tan x = m cã

2) Tõ (IIIa) ta thÊy r»ng : NÕu vµ		lµ hai sè thùc mµ tan , tan
x¸c ®Þnh th× tan =	tan khi vµ	chØ khi cã sè nguyªn k ®Ó
k .

H7 Gi¶i ph−¬ng tr×nh tan 2x tan x.

4. Ph−¬ng tr×nh cot x = m

Cho m lµ mét sè tuú ý, xÐt ph−¬ng tr×nh

cot x = m. (IV)

§KX§ cña ph−¬ng tr×nh (IV) lµ sin x 0. T−¬ng tù nh− ®èi víi ph−¬ng tr×nh tan x = m, ta cã

	NÕu lµ mét nghiÖm cña ph−¬ng tr×nh (IV), nghÜa lµ cot = m th×
		cot x = m x = + k .	(IVa)

VÝ dô 4. Gi¶i c¸c ph−¬ng tr×nh sau :
1) cot x =	1 ;	2) cot 3x = 1.
	3

Gi¶i
1) Gäi lµ mét sè mµ cot =	1	, tøc lµ tan = 3 (ch¼ng h¹n, b»ng b¶ng sè
	3
hoÆc m¸y tÝnh bá tói, ta t×m ®−îc 1,249). Khi ®ã
cot x =	1	x = + k .
	3

2) cot3x = 1 cot3x = cot		3x =		+ k x =		+ k	.	
	4		4		12
							3

chó ý

DÔ thÊy r»ng víi mäi sè m cho tr−íc, ph−¬ng tr×nh cot x = m cã ®óng mét nghiÖm n»m trong kho¶ng (0 ; ). Ng−êi ta th−êng kÝ hiÖu nghiÖm ®ã lµ arccot m (®äc lµ ¸c-c«tang m) Khi ®ã

	cot x = m x =				arccot m + k .
		2x 1		1
H8			tan
	Gi¶i ph−¬ng tr×nh cot	6		3

5. Mét sè ®iÒu cÇn l−u ý

1) Khi ®· cho sè m, ta cã thÓ tÝnh ®−îc c¸c gi¸ trÞ arcsin m , arccos m (víi m 1),

arctan m b»ng m¸y tÝnh bá tói víi c¸c phÝm sin 1 ,	cos 1	vµ tan 1 (xem
bµi ®äc thªm trang 30).

2) arcsin m , arccos m (víi m 1), arctan m vµ arccot m cã gi¸ trÞ lµ nh÷ng sè thùc. Do ®ã ta viÕt, ch¼ng h¹n arctan1 = 4 mµ kh«ng viÕt arctan1 = 45o.

3) Khi xÐt c¸c ph−¬ng tr×nh l−îng gi¸c ta ®· coi Èn sè x lµ sè ®o ra®ian cña c¸c gãc l−îng gi¸c. Trªn thùc tÕ, ta cßn gÆp nh÷ng bµi to¸n yªu cÇu t×m sè ®o ®é cña c¸c gãc (cung) l−îng gi¸c sao cho sin (c«sin, tang hoÆc c«tang) cña

chóng b»ng sè m cho tr−íc ch¼ng h¹n sin(x 20o ) 23 Khi gi¶i c¸c

ph−¬ng tr×nh nµy (mµ l¹m dông ng«n ng÷, ta vÉn gäi lµ gi¶i c¸c ph−¬ng tr×nh l−îng gi¸c), ta cã thÓ ¸p dông c¸c c«ng thøc nªu trªn vµ l−u ý sö dông kÝ hiÖu

sè ®o ®é trong "c«ng thøc nghiÖm" cho thèng nhÊt, ch¼ng h¹n viÕt x = 30o + k360o chø kh«ng viÕt x = 30o + k2 .

Tuy nhiªn, ta quy −íc r»ng nÕu kh«ng cã gi¶i thÝch g× thªm hoÆc trong ph−¬ng tr×nh l−îng gi¸c kh«ng sö dông ®¬n vÞ ®o gãc lµ ®é th× mÆc nhiªn Èn sè lµ sè ®o ra®ian cña gãc l−îng gi¸c.

VÝ dô 5. Gi¶i ph−¬ng tr×nh sin(x + 20o) = 23

Gi¶i
V×	3	= sin60o nªn
V×	2	= sin60o nªn
sin(x + 20o) =			3	sin(x + 20o) = sin60o
sin(x + 20o) =			2	sin(x + 20o) = sin60o
					x 20o 60o k360o	x 40o	k360o

					x 20o 180o 60o k360o	x 100o k360o		

H9 Gi¶i c¸c ph−¬ng tr×nh sau :

1) cos(3x 15o) =	2	;	2) tan 5x = tan 25o.
	2

14. Gi¶i c¸c ph−¬ng tr×nh sau : a) sin 4x = sin 5 ;

c) cos	x	= cos 2 ;

2

x			=		1
b) sin						;
	5				2

					2
d) cos x				=
		18			5

15.a) VÏ ®å thÞ cña hµm sè y sin x råi chØ ra trªn ®å thÞ ®ã c¸c ®iÓm cã hoµnh ®é thuéc kho¶ng ; 4 lµ nghiÖm cña mçi ph−¬ng tr×nh sau

1) sin x =	3	;		2) sin x = 1 ;
1) sin x =	2	;		2) sin x = 1 ;
	2
b) Còng c©u hái t−¬ng tù cho hµm sè y cos x ®èi víi mçi ph−¬ng tr×nh sau
1) cos x = 1	;			2) cos x = 1.
2
16. T×m nghiÖm cña c¸c ph−¬ng tr×nh sau trong kho¶ng ®· cho
a) sin 2x =	1		víi	0 < x < ;
	2
b) cos(x 5) =			3	víi < x < .
b) cos(x 5) =		2		víi < x < .
		2

17.Sè giê cã ¸nh s¸ng mÆt trêi cña mét thµnh phè A ë vÜ ®é 40o b¾c trong ngµy thø t cña mét n¨m kh«ng nhuËn ®−îc cho bëi hµm sè


d(t) = 3 sin	t 80	+ 12	víi t vµ 0 < t 365.

182

a)Thµnh phè A cã ®óng 12 giê cã ¸nh s¸ng mÆt trêi vµo ngµy nµo trong n¨m ?

b)Vµo ngµy nµo trong n¨m th× thµnh phè A cã Ýt giê cã ¸nh s¸ng mÆt trêi nhÊt ?

c)Vµo ngµy nµo trong n¨m th× thµnh phè A cã nhiÒu giê cã ¸nh s¸ng mÆt trêi nhÊt ?

18.Gi¶i c¸c ph−¬ng tr×nh sau

a) tan 3x = tan		3		;		b) tan(x 15o) = 5 ;
		5
c) tan(2x 1) =			3 ;					1	;
						d) cot 2x = cot
								3
x		o					2
e) cot	20		=		3 ;	f) cot 3x = tan

4							5
19. a) VÏ ®å thÞ cña hµm sè y tan x						råi chØ ra trªn ®å thÞ ®ã c¸c ®iÓm cã hoµnh
®é thuéc kho¶ng ( ; ) lµ nghiÖm cña mçi ph−¬ng tr×nh sau
1) tan x = 1 ;						2) tan x = 0 ;

1) cot x =	3	;	2) cot x = 1.
	3

20.T×m nghiÖm cña c¸c ph−¬ng tr×nh sau trªn kho¶ng ®· cho

a)tan(2x 15o) = 1 víi 180o < x < 90o ;

b) cot 3x =	1	víi	< x < 0.
b) cot 3x =		víi	< x < 0.
3			2
21. Khi gi¶i ph−¬ng tr×nh tan x =				3 , b¹n Ph−¬ng nhËn thÊy
vµ viÕt
tan x =		3				x =		+ k .
tan x =		3	tan x = tan			x =		+ k .
					3		3

3= tan

<<< < Предыдущая 1 23 / 253 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке Class 11

#
01.01.202312.59 Mб1300_20200918025803_lich-su---da-ghep.pdf
#
01.01.20237.06 Mб1301_20201026023852_dai-so---da-ghep.pdf
#
01.01.20237.77 Mб1325_20200918030312_gdcd---da-ghep.pdf
#
01.01.20236.21 Mб1326_20200918103747_cong-nghe---da-ghep.pdf
#
01.01.20235.8 Mб1525_20200918030407_dai-so---nc---da-ghep.pdf
#
01.01.20237.02 Mб1526_20200918104515_hinh-hoc---nc---da-ghep.pdf
#
01.01.202333.01 Mб1527_20200918030728_sinh-hoc---nc---da-ghep.pdf
#
01.01.202315.58 Mб2528_20200918104705_hoa-hoc---nc---da-ghep.pdf
#
01.01.202313.41 Mб1529_20200731054914_hoa-hoc---da-ghep.pdf
#
01.01.20235.06 Mб1530_20200918030451_vat-li---nc---da-ghep.pdf