Прямая в пространстве

Векторное уравнение прямой.Положение прямой L в пространстве можно задать с помощью вектораs, параллельного данной прямой, и точки М_о(r_o), лежащей на данной прямой. Пусть М(r) — произвольная точка прямой L. Очевидно, что векторМ_оМ = колинеарен векторуs. По условию колинеарности

r –r_о=ts,

где t — скаляр (параметр), принимающий для каждой точки М определенное числовое значение (отдо). Полученное уравнение называютвекторным уравнением прямой.

Полагая r =(x,y,z),r_о= (a,b,c),s = (m,n,p) и приравнивая координаты векторов влевой и правой частях векторного уравнения, получимпараметрическоеуравнение прямой L:

x=a+mt, y=b+nt, z=c+pt

Исключая параметр t из параметрического уравнения, получим равенства

,

которые носят название канонического уравнения прямой.

Угол  между прямыми L₁ и L₂ легко найти, зная колинеарные им вектора s₁ и s₂

.

Условие параллельности прямых — , аусловие перпендикулярности — = 0.

Угол между прямой и плоскостью  есть угол, дополняющий до 90^o угол  между векторами N и s. Поэтому

.

Условие перпендикулярности прямой и плоскостиэквивалентно условию колинеарности векторовNиs:

,

а условие параллельности — условию перпендикулярности N и s:

= 0.

Если заданы две точки М₁ и М₂, то любую из них можно принять за базовую, а в качестве вектора s взять вектор М₁М₂. Тогда уравнение прямой, проходящей через две точки, можно записать в канонической форме

.

Прямую можно задать и как пересечение двух плоскостей Р₁ и Р₂, рассматривая два уравнения этих плоскостей как систему:

.

Чтобы получить уравнение этой прямой в канонической форме необходимо найти хотя бы одну общую точку этих плоскостей и вектор, колинеарный этой прямой. В качестве такой точки можно взять точку пересечения прямой с, например, плоскостью ХОУ, уравнение которой имеет очень простой вид — z=0. Подставляя это значение в систему, получим два уравнения с двумя неизвестными

.

Решение этой системы и даст необходимые координаты х=а и у=b, и тогда искомой точкой будет (а,b,0). В качестве вектора s можно взять векторное произведение N₁xN₂ , так как оно является вектором параллельным и той и другой плоскости, а следовательно параллельно прямой, по которой они пересекаются.

Пример. Привести к каноническому виду уравнение прямой, заданной пересечением двух плоскостей

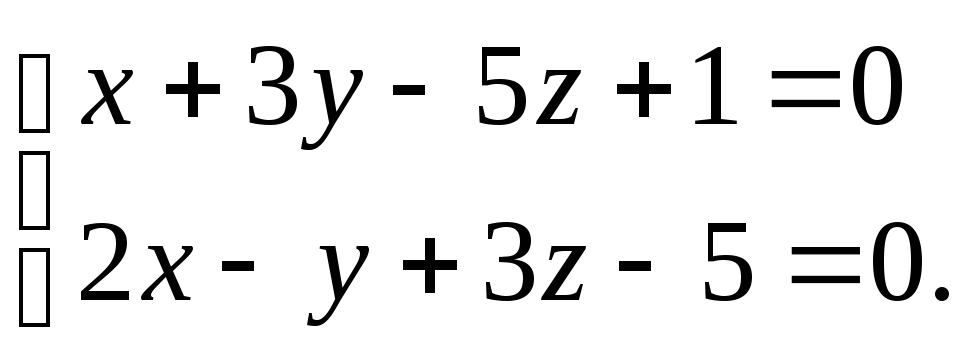
Положим z=0. Тогда получим систему

Решением будут х =2 и у=-1. Координаты базовой точки (2,-1, 0).

Найдем теперь вектор s = N₁xN₂ :

,

То есть вектор s имеет координаты (3,-13,-7). Следовательно искомое уравнение прямой имеет вид:

.