Элементы аналитической геометрии

Предметом аналитической геометрии являются кривые и поверхности, которые изучаются при помощи алгебры. В основе исследований лежит метод координат, который определяет положение точки в пространстве с помощью чисел — координат этой точки. Каждая кривая или поверхность описывается одним или несколькими уравнениями, связывающими координаты точки, принадлежащей данному объекту. Геометрические свойства кривых или поверхностей описываются также уравнениями, связывающими координаты с некоторыми постоянными величинами — параметрами, которые в свою очередь определяют положение, форму, размер и другие характеристики объектов. Эти факты позволяют изучать геометрические объекты аналитическим (и в частности алгебраическим) методом.

При изучении геометрических объектов мы будем опираться на понятие вектора. Векторная величина характеризуется не только числовым значением, но и направлением в пространстве. Естественным изображением вектора служит направленный отрезок со стрелкой на одном из концов:

Длина отрезка равна неотрицательному числовому значению (модулю) вектора в выбранном масштабе, а направление указывается стрелкой. Для определения направления вектора необходимо иметь систему координат, которая может быть задана различными способами. В данном курсе мы будем использовать декартовые прямоугольные системы координат.

Координаты на прямой, на плоскости и в пространстве.

Координаты на прямой. Пусть задана некоторая прямая. Положение точки на этой прямой можно задать следующим образом. Отмечается произвольная начальная точка О и одно из направлений указывается как положительное. Такая конфигурация называется осью:

«—» «+»

О Е М Х

На оси выбирается также единица масштаба — произвольный отрезок ОЕ. Тогда положение точки М на оси ОХ определяется числом х, абсолютная величина которого равна расстоянию от М до О, выраженному в выбранной единице длины.х>0, если ОМ направлен в сторону возрастания Х, их<0, если в противоположную сторону. Такое числохназывают координатой точки М. Каждой точке оси ОХ соответствует единственное вещественное число и обратно, любому вещественному числу соответствует единственная точка оси. Говорят, что между вещественными числами и точками оси установленовзаимно-однозначное соответствие.

Довольно часто приходится изменять положение начальной точки отсчета с О на О’ — то есть выполнять перенос начала координат. Пусть О’ имеет координату х_оотносительно О, а точка М — координатух’относительно О’. Тогда очевидны соотношения

х’ =х -х_о х =х’+х_о

Эти формулы справедливы для любых х их_о и называются формулами перехода от старой к новой системе координат и обратно.

Точка М с координатой х обозначают символом М(х). Согласно определению расстояние ОМ равнох. Найдем теперь расстояние между точками М₁(х₁) и М₂(х₂). Для этого перенесем начало координат в точку М₁и, применяя формулы перехода к системе с новой начальной точкой, получим

х₂’ =х₂–х₁

Но длина М₁М₂есть расстояние точки М₂ от нового начала координат М₁М, то есть

d =М₁М₂ =х₂–х₁=

Деление отрезка в заданном отношении. Говорят, что точка М делит отрезок М₁М₂в отношении, взятому со знаком «плюс» если отрезки М₁М и ММ₂ направлены по прямой в одну сторону и со знаком “минус”, если их направления противоположны. Отметим, что точка М не может совпадать с точкой М₂, так как тогда длина ММ₂будет равна нулю. Кроме того точка М₁не должна совпадать с М₂. Другими словами-1. Выражая длины отрезков через координаты точек, получим

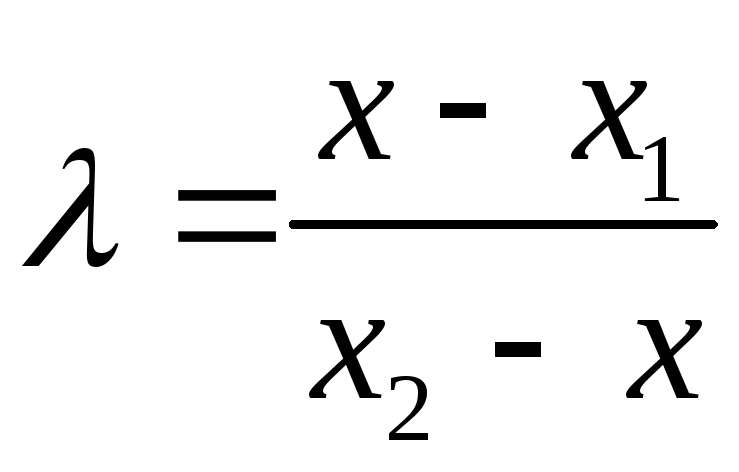
Разрешая последнее равенство относительно хполучим:

Последние равенства позволяют найти координату точки М, которая делит отрезок в заданном отношении , или отношение, если задана координата точки. В частном случае, координату середины отрезка (=1) вычисляют по формулех=(х₁+х₂)/2 .

Координаты на плоскости. Для определения положения точки М на плоскости через произвольную точку плоскости О проводят две взаимно перпендикулярные прямые. На каждой прямой задают положительные направления, указываемые стрелкой. Получаются две координатных оси с общим началом О. Ось ОХ называют осью абсцисс, а ось ОУ — осью ординат. Единицей масштаба по обеим осям служит отрезок ОЕ:

Пусть теперь задана точка М, а М_х и М_у — проекции этой точки на оси ОХ и ОУ соответственно. Напомним, что проекцией точки на прямую называют основание перпендикуляра опущенного из данной точки на прямую. Числа х=М_х и у=М_у называют координатами точки М или ее абсциссой и ординатой соответственно. Построенную систему координат называют прямоугольной или декартовой.

Система координат ХОУ называется правой если кратчайший поворот от оси ОХ к оси ОУ происходит против часовой стрелки. В противном случае систему ХОУ называют левой. Оси координат разбивают координатную плоскость на четыре квадранта, которые нумеруются обычно римскими цифрами против часовой стрелки. В первом квадранте координаты х и у неотрицательны.

Для обозначения точки М имеющей координаты х и у применяют символ М(х, у). Зная координаты точки М ее положение на плоскости можно найти как пересечение перпендикуляров восстановленных к осям ОХ и ОУ в точках х и у соответственно. Задавая же положение точки нетрудно найти ее координаты. Таким образом между точками координатной плоскости и упорядоченными парами вещественных чисел устанавливается взаимно-однозначное соответствие.

Для упрощения уравнений изучаемых кривых часто выполняется перенос начала координат в новую точку, а направления осей сохраняются. Другими словами выполняется переход от системы ХОУ к параллельной системе Х’О’У’. Выведем формулы, связывающие старые координаты х и у с новыми — х’ и у’.

Пусть новое начало координат О’ имеет в старой системе координаты х_о и у_о. Построим проекции точки М(х, у) и О’ на новые и старые оси координат

Очевидны следующие формулы перехода от старой системы к новой:

х’ = х – х_о , у’ = у – у_о ;

и формулы обратного перехода:

х = х_о + х’,у = у_о + у’.

Расстояние от начала координат О до точки М находится по теореме Пифагора:

d = ОМ =.

Пусть теперь требуется найти расстояние между точками М₁(х₁,у₁) и М₂(х₂,у₂). Перенесем начало координат в точку М₁, тогда

d’ = М₁М₂=.

Но так как х’ = х₂ – х₁ , у’ = у₂ – у₁ , то

d’ = М₁М₂=.

Пусть теперь дан отрезок М₁М₂ и требуется найти точку М, которая делит в отношении. Для решения задачи спроектируем точки М_{1 ,} М₂и М на оси ОХ и ОУ. Точка х делит отрезок х₁х₂, в том же отношении, что и точка М отрезок М₁М₂(по теореме о сторонах угла, пересекаемых параллельными прямыми). Поэтому

Используя формулу для нахождения координаты точки М для отрезка на прямой, получим

и, в частности, для координат середины отрезка х_с, у_с имеем:

х_с=(х₁+х₂)/2, у_с=(у₁+у₂)/2.

Зная координаты вершин треугольника, можно довольно просто вычислить его площадь. Покажем как это можно сделать. Пусть вершины треугольника АВС лежат в первой четверти и пронумерованы в порядке возрастания абсцисс, то есть х₁<х₂<х₃. Возможны 2 варианта расположения треугольника:

1-й вариант 2-й вариант

В первом случае ,

а во втором – .

Используя теперь формулу для нахождения площади трапеций, в которых ординаты вершин треугольника являются основаниями, а разности абсцисс — высотами, после несложных вычислений получим

.

Значение выражения не меняется при круговой перестановке индексов и следовательно нумерация вершин в порядке возрастания абсцисс не обязательна. Требование принадлежности треугольника первому квадранту также не обязательно, потому что всегда можно найти новую систему координат, в которой он будет лежать именно в первом квадранте.

Следствие.Если точки A, B и C лежат на одной прямой, то S_ABC =0.

Полярные координаты. Положение точки на плоскости можно задавать и с помощью так называемых полярных координат. В этом случае на плоскости фиксируется произвольная точка О — полюс системы, из которой проводится луч ОР — полярная ось с указанием единичного отрезка ОЕ. Тогда положение точки М определяется ее расстояние от полюса r и углом, который образует отрезок ОМ с лучом ОР:

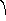
 M(r,)

r

О Е Р

r называют радиусом-вектором точки М, а — ее полярным углом. Полюс О имеет r=0, и не имеет угла. Полярный угол положителен при отсчете угла против часовой стрелки и отрицателен при отсчете по часовой. Радиус-вектор неотрицателен — r0. Допуская, чтолюбое действительное число мы неявно допускаем, что любой точке М соответствует бесчисленное множество полярных углов, отличающихся друг от друга на 2k, где k — целое число. В обратном же направлении соответствие однозначное. Значенияиз отрезка [0;2] называют главными значениями полярного угла, а система полярных координат (r,), в которой r0 и[0;2], называется основной.

Выведем теперь формулы перехода от полярных координат к декартовым и обратно. Для этой цели совместим начала обеих систем и направим ось ОХ по полярному лучу ОР:

Тогда справедливы следующие соотношения:

х = r cos , y = r sin — формулы перехода от полярной системы координат к декартовой. Формулы обратного перехода:

r=,

cos  =,

sin =, или = arctg (y/x).

Координаты в пространстве. Как и в предыдущих случаях в пространстве выбирается произвольная точка О, которая будет служить началом координат и началом отсчета. Через точку О проводятся три взаимно-перпендикулярные оси: ОХ — ось абсцисс, ОУ — ось ординат и ОZ — ось аппликат. На каждой оси стрелкой указываются положительные направления и задается единица масштаба ОЕ. Координатные оси попарно определяют три координатных плоскости: ХОУ, ХОZ и УОZ. Система координат ХОУZ называется правой, если кратчайший поворот от оси ОХ к оси ОУ происходит против часовой стрелки, если смотреть на него с положительного направления оси OZ. В противном случае систему координат называют левой. В основном мы будем работать с правыми системами.

Положение точки М определяют ее проекции на координатные оси М_х, М_у и М_z , которые и называют ее координатами х, у, z или ее абсциссой, ординатой и аппликатой соответственно. M_xy — проекция М на плоскость ХОУ. Три координатных плоскости делят все пространство на 8 октантов.

Переход к новому началу координат О’(x_o,y_o,z_o) с параллельным переносом осей выполняется по формулам:

х’ = х – х_о , у’ = у – у_о, z’ =z –z_о

а формулы обратного перехода имеют вид:

х = х_о + х’,у = у_о + у’, z = z_о + z’.

Расстояние ОМ точки М от начала координат О, между точками М₁ и М₂ определяются формулами:

d = ОМ = , М₁М₂ =

Формулы для нахождения координат точки М, делящей отрезок М₁М₂в отношенииимеют вид:

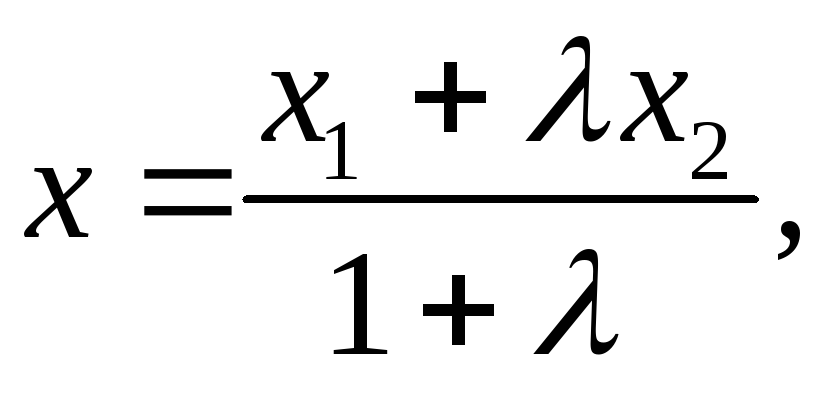
и, в частности, для координат середины отрезка х_с, у_с,z_с имеем:

х_с=(х₁+х₂)/2, у_с=(у₁+у₂)/2,z_с=(z₁+z₂)/2