
- •Линейная алгебра и функции
- •Операции над матрицами.
- •Определители и их свойства.
- •Свойства определителей.
- •Обратная матрица и алгоритм ее вычисления.
- •Понятие о ранге матрицы
- •Системы линейных уравнений. Решение и исследование системы трех линейных уравнений с тремя неизвестными.
- •Однородная система трех линейных уравнений с тремя неизвестными.
- •Решение произвольных систем линейных уравнений
- •Решение однородных систем линейных уравнений
- •Решение систем линейных уравнений методом Гаусса
- •Модель многоотраслевой экономики (балансовый метод или модель Леонтьева)
- •Многомерные вектора и векторные пространства
- •Размерность и базис векторного пространства
- •Переход к новому базису
- •Евклидово пространство
- •Линейные операторы
- •В силу линейности оператора Аполучаем
- •Собственные векторы и собственные значения линейного оператора
- •Квадратичные формы
- •Модель международной торговли
Обратная матрица и алгоритм ее вычисления.
Матрица
![]() называетсяобратной
по отношению к матрице
называетсяобратной
по отношению к матрице
![]() ,
если выполняются равенства
,
если выполняются равенства

Прямая
и обратная матрицы, как и единичная
матрица
![]() ,
являются квадратными.
,
являются квадратными.
Матрица
![]() называетсявырожденной
или особой,
если ее определитель
называетсявырожденной
или особой,
если ее определитель
![]() .
В противном случае
.
В противном случае![]() матрицу
матрицу![]() называютневырожденной
или неособой.
называютневырожденной
или неособой.
Необходимое и достаточное условие существования обратной матрицы дает следующая теорема:
Теорема:
Обратная матрица
![]() существует и является единственной
тогда и только тогда, когда матрица
существует и является единственной
тогда и только тогда, когда матрица![]() не вырождена, т.е.
не вырождена, т.е.![]() .
.
Необходимость:
Пусть
![]() существует. Тогда, по определению,
существует. Тогда, по определению,
![]() .
.
По свойству определителя произведения двух матриц имеем
![]() .
.
Следовательно,
![]() .
.
Достаточность:
Пусть
![]() - не вырождена, т.е.
- не вырождена, т.е.![]() .
Введем так называемуюприсоединенную
квадратную
матрицу
.
Введем так называемуюприсоединенную
квадратную
матрицу
![]() ,
составленную из алгебраических
дополнений, элементов транспонированной
матрицы
,
составленную из алгебраических
дополнений, элементов транспонированной
матрицы![]() .
Элементами присоединенной матрицы
будут
.
Элементами присоединенной матрицы
будут
![]() .
.
Умножим
теперь
![]() на
на![]() :
:

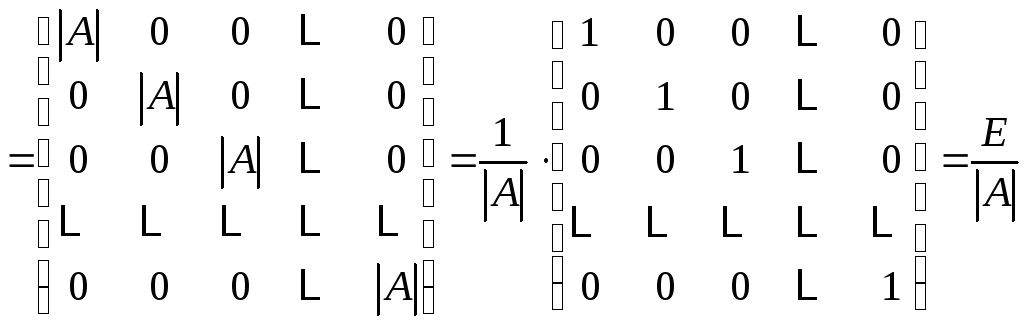 .
.
Таким образом,
 или
или
 ,
,
поэтому
можно принять за
 .
.
Алгоритм
нахождения
![]() .
.
Вычислить определитель

Транспонировать матрицу
 (найти
(найти ).
).Вычислить алгебраические дополнения для всех элементов матрицы
 -
- и составить сопряженную матрицу
и составить сопряженную матрицу .
.Разделить матрицу
 на
на ,
т.е. найти
,
т.е. найти
 .
.
Выполнить проверку правильности вычислений
![]() .
.
Понятие о ранге матрицы
Пусть
дана произвольная матрица
![]() .
Из элементов этой матрицы вычеркиванием
строк и (или) столбцов можно получить
множество квадратных матриц размерностью
.
Из элементов этой матрицы вычеркиванием
строк и (или) столбцов можно получить
множество квадратных матриц размерностью![]() от 1 до наименьшего из значений
от 1 до наименьшего из значений![]() и
и![]() :
:
![]() .
.
Определители
этих квадратных матриц называют минорами
матрицы
![]() соответствующего порядка
соответствующего порядка![]() .
.
Рангом
матрицы
![]() называют наивысший порядок отличного
от нуля минора, полученного из матрицы
называют наивысший порядок отличного
от нуля минора, полученного из матрицы![]() вычеркиванием строк и (или) столбцов.
Для обозначения ранга матрицы А
используются символы
вычеркиванием строк и (или) столбцов.
Для обозначения ранга матрицы А
используются символы
![]()
Элементарными преобразованиями матрицы называют следующие операции:
Отбрасывание нулевых строк и (или) столбцов.
Умножение элементов строки или столбца на отличный от нуля скаляр.
Перестановка строк или столбцов.
Прибавление к строке (столбцу) линейной комбинации других строк (столбцов).
Транспонирование матрицы.
Теорема. Элементарные преобразования не изменяют ранг матрицы.
Элементарные
преобразования позволяют привести
матрицу
![]() (или
(или![]() )
к ступенчатому виду:
)
к ступенчатому виду:
 ,
,
при
котором
![]() и
и![]() ,
где
,
где![]() .
.
Очевидно,
что ранг ступенчатой матрицы равен
![]() ,
так как по крайней мере один минор
,
так как по крайней мере один минор![]() -го
порядка в левой части матрицы равен
произведению ненулевых диагональных
элементов и, следовательно, отличен от
нуля.
-го
порядка в левой части матрицы равен
произведению ненулевых диагональных
элементов и, следовательно, отличен от
нуля.
Ранг суммы матриц подчиняется неравенствам:
![]()
Ранг
произведения
![]() на
на![]() не превосходит наименьшего из рангов
матриц
не превосходит наименьшего из рангов
матриц![]() и
и![]() :
:
![]() .
.
В
частности, если
![]() и
и![]() - квадратные матрицы и определитель
- квадратные матрицы и определитель![]() ,
то
,
то
![]() .
.
Отметим также, что
![]() .
.
Пусть
задана произвольная матрица
![]() :
:
 .
.
Каждую
строку
![]() этой матрицы можно представить
матрицей-строкой
этой матрицы можно представить
матрицей-строкой![]() :
:
![]()
![]() .
.
Арифметические операции над матрицами-строками выполняются по общим для матриц правилам. Например
![]() ,
,
![]() .
.
Используя
введенные обозначения для строк матрицы
![]() ,
мы можем представить ее в виде
матрицы-столбца
,
мы можем представить ее в виде
матрицы-столбца
 ,
,
в
которой элементами служат, в свою
очередь, матрицы-строки
![]() .
.
С помощью введенных обозначений уточним понятие линейной зависимости (или независимости), а также линейной комбинации строк матрицы.
Говорят, что строка
![]() является линейной комбинацией строк,
например,
является линейной комбинацией строк,
например,![]() ,
если выполняется равенство
,
если выполняется равенство
![]() ,
,
в
котором
![]() - произвольные числа. В частности, нулевая
строка всегда есть линейная комбинация
всех остальных, если положить все
- произвольные числа. В частности, нулевая
строка всегда есть линейная комбинация
всех остальных, если положить все![]() .
.
Говорят,
что строки
![]() линейно-зависимы, если существуют не
равные нулю одновременно числа
линейно-зависимы, если существуют не
равные нулю одновременно числа![]() такие, что
такие, что
![]() .
.
Допустим,
что
![]()
![]() .
Тогда
.
Тогда
![]() или
или
 ,
,
где
 ,
,![]() ,
,![]() ,
т.к.
,
т.к.![]() не присутствует в правой части.
не присутствует в правой части.
Другими
словами, если строки
![]() линейно-зависимы, то мы всегда можем
представить хотя бы одну из них в виде
линейной комбинации остальных. Если же
указанные строки линейно-независимы,
то их линейная комбинация может быть
равна нулю только в том случае, когда
всеi.
линейно-зависимы, то мы всегда можем
представить хотя бы одну из них в виде
линейной комбинации остальных. Если же
указанные строки линейно-независимы,
то их линейная комбинация может быть
равна нулю только в том случае, когда
всеi.
Теорема: Ранг матрицы равен максимальному числу ее линейно-независимых строк (или столбцов), через которые выражаются все ее остальные строки (столбцы).
Доказательство:
Пусть
![]() .
Тогда существует хотя бы один ненулевой
минор
.
Тогда существует хотя бы один ненулевой
минор![]() -го
порядка. Не нарушая общности, будем
считать, что он расположен в левом
верхнем углу
-го
порядка. Не нарушая общности, будем
считать, что он расположен в левом
верхнем углу![]() :
:
 .
.
Тогда
строки
![]() - линейно-независимы. Проведем
доказательство от противного. Пусть
- линейно-независимы. Проведем
доказательство от противного. Пусть![]() - линейная комбинация остальных строк,
т.е.
- линейная комбинация остальных строк,
т.е.
![]() .
.
Вычтем
теперь из
![]()
![]() ,
затем
,
затем![]() ,…,
и, наконец,
,…,
и, наконец,![]() .
В результате получим
.
В результате получим![]() и след
и след![]() ,
что противоречит условию теоремы.
,
что противоречит условию теоремы.
Следовательно,
![]() - линейно-независимы. Эти строки, как и
исходный минор
- линейно-независимы. Эти строки, как и
исходный минор![]() -го
порядка называютбазисными.
-го
порядка называютбазисными.
Покажем
теперь. Что любая небазисная строка
матрицы
![]() линейно-зависима, т.е. линейно выражается
через базисные.
линейно-зависима, т.е. линейно выражается
через базисные.
Рассмотрим
минор
![]() -го
порядка, полученный добавлением
-го
порядка, полученный добавлением![]() -той
строки и
-той
строки и![]() -того
столбца к минору порядка
-того
столбца к минору порядка![]() :
:
 ,
,
![]() и
и![]() .
.
Разложим теперь этот минор по элементам последнего столбца:
![]()
![]() ,
т.к. это базисный минор порядка
,
т.к. это базисный минор порядка
![]() .
Поэтому мы можем разделить последнее
равенство на
.
Поэтому мы можем разделить последнее
равенство на![]() и выразить из него элемент
и выразить из него элемент![]() :
:
 .
.
Отсюда
видно, что для любого
![]() и
и![]() элементы
элементы![]() -той
строки линейно выражаются через
соответствующие элементы строк
-той
строки линейно выражаются через
соответствующие элементы строк![]() ,
т.е. Она является их линейной комбинацией.
,
т.е. Она является их линейной комбинацией.
