Приближённое решение уравнений. Интерполирование функций. Действительные корни .

Пусть дано уравнение , гдедифференцируемая функция. Требуется найти все действительные корни с заданной точностью.

Графический способ. Приведём к видугдеОба эти уравнения равносильны, т.е. имеют одни и те же корни. Распределение членов выполняется с учётом простоты построения графикови. Например:гдеиДлягдеи

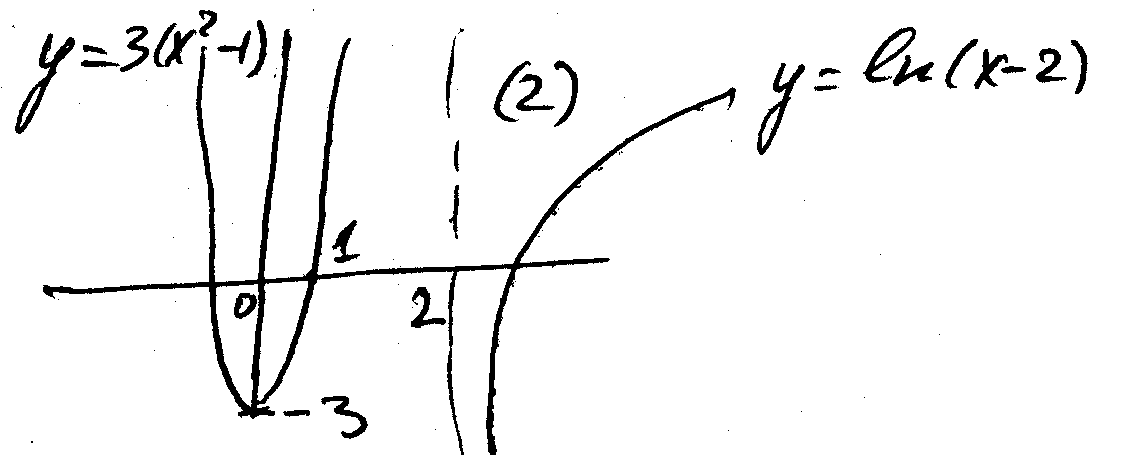После этого строятся графикиина одной координатной плоскости. Абсциссы точек пересечения этих кривых будут корнями уравненияа следовательно, ит.к. в общей точкеиОтсутствие общих точек означает отсутствие действительных корнейТ.о. это построение даёт возможность определить число действительных корней и их приближённые числовые значения.

В случае (1) мы имеем 2 действительных корня и, в (2) – нет. Зная теперь приближённые значения корней (1) «отделим» точные корни, т.е. построим тесные числовые промежуткив каждом из которых содержится только один точный корень. Предположим,изменяет знак в любом корне. На самом деле это не всегда так, но…

На рис.1 видно, что изменяет знак в т.с «+» на «-», а в- с «-» на «+».

Приближённое значение нозначит точное значениеВозьмём, например,тогдатогда в промежуткеизменяет знак и, будучи непрерывной, обращается в 0 на этом промежутке. Причём только 1 раз, т.к.имеет только 1 отрицательный корень. Следовательно, точный кореньГоворят, что«отделён» с помощью этого промежутка.

Приближённое значение носледовательно,Но привесть точный, единственный корень

Т.о. отделены оба действительных корня Числа –2 и –1 – приближённые значения- по недостатку и избытку соответственно, а 0 и 1 – приближённые значения

Построенные прмежутки можно «сужать» и тогда новые отрезки (границы) будут давать всё более точные приближённые значения корней. Метод деления отрезка пополам.

Методы уточнения приближённого корня.

Метод Ньютона (касательных). Пустьимеет корень, отделённый промежуткоми пустьдважды дифференцируема на. Рассмотрим график. Проведём вкасательнуюимеющую уравнениеЭта касательная пересечётОХ в точке с абсциссой Докажем, чтоесливозрастает, т.еит.е. вогнута. При этих условиях, учитывая, чтонаполучим

Т.к. также возрастает. Изимеем

а по формуле Лагранжа

где аТ.к.т.е.

или Ч.Т.Д.

Следовательно, и поэтомуболее точное приближение, чемЗаменяянаможно повторить эту процедуру и найти

которое находится между иПродолжая процесс, получим последовательность

где (*)

Теорема. Последовательность имеет пределом точный кореньуравнения

Доказательство. Т.к. монотонно убывающая, тодляи имеет пределПокажем, что

т.е. С – есть корень т.к.единственный корень в

Метод уточнения корня с помощью формулы (*) называют методом Ньютона.

Итак метод Ньютона применим, если в промежутке содержится только 1 корень уравненияне должна иметь экстремумов и точек перегиба, т.е.иКроме того, графикдолжен пересекать осьХ, т.е. При этих условиях гарантируется существование области, которая распологается слева или справа от, в зависимости от того, где будут одинаковы знакии

Эти условия являются достаточными. Т.е. рпи их нарушении может случиться так, что корень всё же находится по методу Ньютона.

Оценим теперь абсолютную погрешность го приближения

где конец отрезкакоторый не принадлежит области

По формуле Лагранжа

но

Т.к. знакопостоянна, томонотонно врзрастает или убывает и во всех случаяхимеет наименьшее значение вПоэтому, заменяянаи получаем равенство (*).

Если имеет несколько действительных корней, то любой корень уточняется отдельно.

Метод хорд. Пусть точный кореньиЕсли построить хорду, то абсциссаточки пересечения этой хорды сОХ будет более близко к , чем нулевые приближенияи.

Уравнение хорды

полагая получим

или

где

Вычислим теперь и из двух отрезковивыберем тот, на концах которогоимеет противоположные знаки, т.е. тот, который содержитПродолжая процесс, получим последовательностьпри

Абсолютная погрешность го приближения оценивается по формуле

где наименьшее значениена отрезке

По формуле Лагранжа имеем

где

но

Метод итерации. Пусть имеет кореньРазрешимотносительно

(*)

Пусть и

(А) где

Геометрически эти требования значат, что график должен быть монотонно возрастающим или убывающим в промежуткеи притом должен располагаться более «полого» чем биссектриса 1-го координатного угла(есливозрастает) и более «полого» чемеслиубывает.

Приводя к виду (*) мы преобразуем тождествок видут.е. корнем

будет абсцисса точки , пересечения графикас

Приведение к виду (*) можно выполнить различными способами. Например::и т.д. Однако нужны только те преобразования, при которых выполняется (А). Подходящий вид находится методом проб. Так длядля корня в промежуткевидявляется неподходящим, т.к.а вид- не удовлетворяет (А), т.к.для

Если условие (А) соблюдается, то метод итераций позволяет вычислить корень с любой точностью. В качестве начального приближения можно выбрать любой из

Метод итераций заключается в следующем:

(*)

Теорема. Если знакопостоянна наи по абсолютной величине строго меньше 1, т.е.гдето последовательность (*) приимеет своим пределом точный корень, где

Доказательство. Пусть окрестность симметрична относительно(Этого всегда можно достинуть, зная). Обозначим её черезСоставим разности между членамии числоми преобразуем их по формуле Лагранжа, учитывая, что

где

Т.к. т.е.причёмближе кчемДалее

т.е. ещё ближе кчемПродолжая этот процесс получим

Теперь заметим, что т.к. всеПоэтому

или

Рассмотрим теперь

т.к.

Ч.Т.Д.

Можно также доказать, чтомонотонно прии колеблется околопри

Абсолютная погрешность го приближения оценивается неравенством:

где

Действительно

­

но

Проверку абсолютной погрешности целесообразно проводить на любом шаге вычислений, если заранее известна величина !

Комбинированный способ уточнения корня. Суть метода заключается в одновременном применении метода хорд и метода касательных на отрезке Метод основан на том, что при выполнении условий применимости метода касательныхметоды хорд и касательных дают приближения по разные стороны от точного значения. Поэтому после любого шага мы получаем корень с избытком и с недостатком и эти значения могут быть использованы в качестве новых приближений илиидающих новый отрезок выделения.