Асимптоты.

Довольно часто требуется исследовать форму кривой при неограниченном возрастании. Важным частным случаем является тот, когда исследуемая кривая при удалении её переменной точки в бесконечность (т.е. прирасстояния от начала координат до этой точки) неограниченно приближается к некоторой прямой.

Определение. Прямая А называется асимптотой кривой, если расстояние от точкидо этой прямой стремится к нулю.

Различают вертикальные асимптоты – т.е. параллельные OY, горизонтальные – т.е. параллельные OX и наклонные, т.е. не параллельные OY или OX.

1. Вертикальные асимптоты. Из определения следует, что если

,

то прямая есть асимптота кривой, и обратно, что еслиесть асимптота, то выполняется одно из написанных равенств.

Следовательно, для нахождения вертикальных асимптот нужно найти такие , чтобы при. Тогдаи будет асимптотой.

Пример. ,- асимптота, т.к.,.

- б.м. вертикальных асимптот,,

т.к. при .

2. Наклонные асимптоты. Пусть имеет наклонную асимптоту

1. .

Определим коэффициенты и. Пустьи.расстояние отдо. По условию

2. 

Пусть - угол наклонак осииз; т.к., то

(2’) .

При этом из (2)(2’) и наоборот. С другой стороны,

и (2’) приобретает вид:

3. .

Итак, если (1) есть асимптота, то выполняется (3) и, наоборот, если выполняется (3), то (1) – уравнение асимптоты.

Определим теперь и. Выносяза скобки, получим

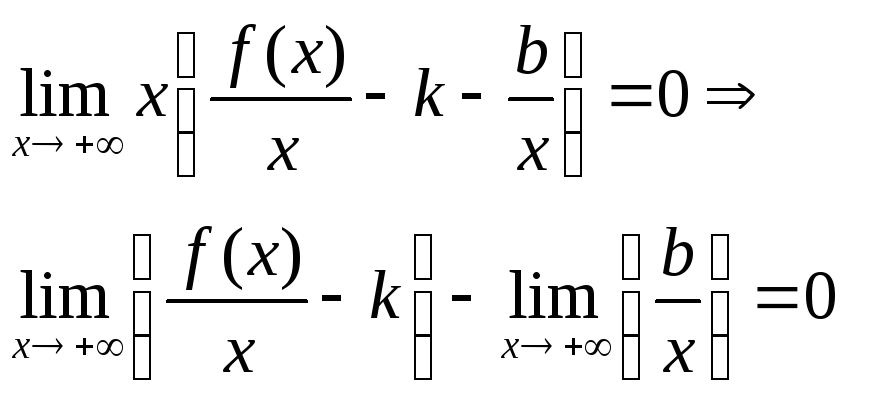
Т.к. или

Зная теперь можно найти ииз (3)

Итак, если есть асимптота,

(*)

Обратное также справедливо. Если существуют пределы (*), то есть асимптота. Если же хотя бы один из пределов не существует, тоасимптоты не имеет.

Пример.

1. Найдём вертикальные асимптоты:

- вертикальная асимптота.

2. Ищем наклонные асимптоты:

- асимптота.

Пример. , вертикальных нет,

при,

при асимптоты нет.

Общий план исследования функций и построения графиков.

Под «исследованием функции» обычно понимается нахождение:

1. естественной области существования функции;

2. точек разрыва функции; нули функции?

3. интервалов возрастания и убывания функции;

4. точек максимума и минимума и экстремальных значений функции;

5. областей выпуклости и вогнутости графика, точек перегиба;

6. асимптот графика функции.

На основании проведённого исследования строится график. Целесообразно помечать элементы графика параллельно с исследованием.

Замечание 1. Если - чётная, т.е.достаточно исследоватьи строить её график дляОДЗ, т.к. график симметриченOY.

Замечание 2. Если - нечётная, т.е.также достаточно провести исследование для. График симметричен относительно начала координат.

Замечание 3. Т.к. одни свойства функции могут определять другие, то порядок исследования можно изменять, исходя из конкретного вида исследуемой функции. Например, если непрерывна и дифференцируема и найдены точки максимума и минимума, то тем самым определены области убывания и возрастания.

Пример. Исследовать и построить её график.

Исследование кривых, заданных параметрами.

Пусть , исследуем аналогично.

1. Вычисляем

и .

2. Для точек кривой, вблизи которых кривая является графиком некоторой функции , вычисляем

.

3. Находим 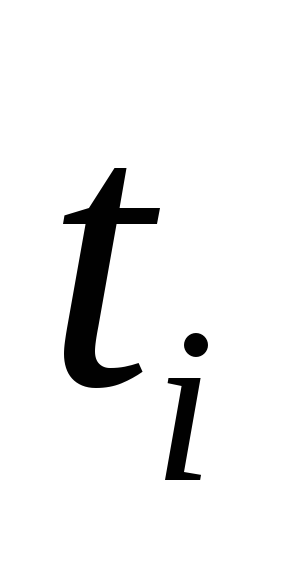, при которых хотя бы одна из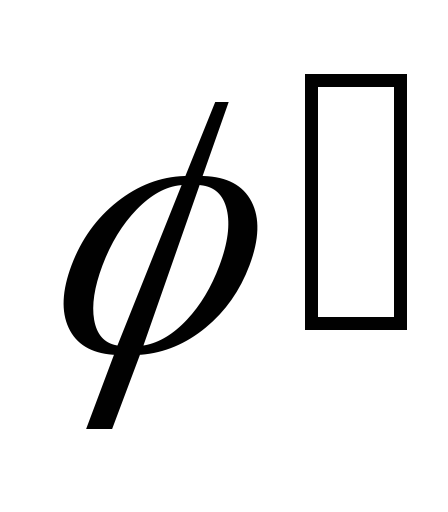илиобращается в нуль или терпит разрыв, следовательно,- критические точки. Затем в любом интервале, (а следовательно, и в любом) определяем знаки тем самым находим области возрастания и убывания. Это даёт также возможность определить характер точек, соответствующих.

4. Далее находим

и исследуя на знак, определяем направления выпуклости кривой на любом интервале.

Для нахождения асимптот находим такие , что приилиили, или ии.

Затем исследование проводится обычным способом. Другие особенности поясним на примерах.

Пример.

(1’)

иопр. для, но в силу периодичности. Тогдаикривая асимптот не имеет.

Далее

(*) при

(**)

На основании (*) и (**) составим таблицу:

обл. изм. t	x	y	Знак	убыв., возр.
			-	убыв.
			+	возр.
			-	убыв.
			+	возр.

Из таблицы следует, что (1) определяет 2 непрерывных : прии при.

Из (**) следует, что и, т.е. в этих точках касательная квертикальна. В точках же, т.е. касательная к- горизонтальна. Далее:

при- кривая вогнутая,

при- кривая выпуклая.

(астроида)