6.2. Свойства функций, непрерывных в точке

1. Если функции y=f(x) и y=g(x) непрерывны в точке , тоf(x) + g(x);

f(x)  g(x); (g()0) также непрерывны в точке .

2. Если функция y=f(x) непрерывна в точке иf ()0, то существует окрестность этой точки, для всех х из которой f (х)0.

3. Если функция y=f(U) непрерывна в точке , функцияU=g(x) непрерывна в точке (=g()), то сложная функцияy=f(g(x)) непрерывна в точке 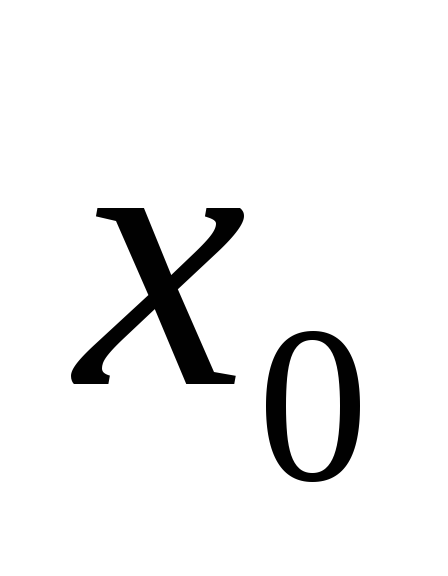и можно записать:

6.3. Свойства функций, непрерывных на отрезке

^{1. Если функция непрерывна на отрезке, то она ограничена на этом отрезке (рис. 2.6.)}

у

y=f(x)

b х

Рис. 6.6. Непрерывная функция ограничена на отрезке

2. Если функция непрерывна на отрезке, то она достигает на нем наименьшее m и наибольшее M значения (рис. 6.7.).

у

M

y=f(x)

b

х

m

Рис. 6.7. Непрерывная функция достигает на отрезке наименьшее и наибольшее значения

3. ^{Если функция непрерывна на отрезке и на концах его достигает значения разных знаков, то внутри отрезка существует хотя бы одна точка, в которой функция обращается в нуль (рис. 2.8.).}

^{у f(a)f(b)0}

f(c)=0

y=f(x)

b

0 а с х

Рис. 6.8. Непрерывная функция обращается в нуль внутри отрезка, если на концах его имеет значения разных знаков