Прямая на плоскости

Уравнение прямой с угловым коэффициентом. Пусть в координатной плоскости ХОУ задана произвольная прямая L не параллельная оси ОУ. Тогда ее положение можно определить ординатой b точки пересечения прямой с ОУ и углом, который она образует с положительным направлением оси ОХ.

Очевидны следующее равенство:

y - b = x tgилиy = kx + b, где

k = tg. Уравнение

y = kx + b

и называют уравнением с угловым

коэффициентом.

Если прямая проходит через начало координат, то ее уравнение имеет вид y = kx. Если прямая параллельна оси ОХ, тоy = b. Если же она параллельна оси ОУ, тох = а.

Общее уравнение прямой. Покажем, что любое уравнение первой степени относительно переменныхх и у

Ах+ Ву+ С = 0

является уравнением некоторой прямой. Рассмотрим три случая:

1) В 0, тогдау= (-А/В)х+ (-С/В). Полагаяk= (-А/В) и

b= (С/В), получим уравнение прямой с угловым коэффициентом;

2) В = 0, тогда Ах+ С = 0 илих= (-С/А) =а: прямая параллельна ОУ;

3) А = 0, тогда Ву+ С = 0 илиу= (-С/А) =b: прямая параллельна ОХ.

При А=В=0 уравнение теряет смысл, так как не будет содержать переменных.

Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых. Пусть уравнениями с угловым коэффициентом заданы две прямые:

y = k₁x + b₁иy = k₂x + b₂,

Требуется найти угол между ними.

Пусть ₁и₂— углы образованные прямыми с осью ОХ. Тогда угол между прямымибудет равен (₂-₁) или (- (₂-₁)). Так как[0;/2] иtg— неотрицателен, то

.

Если прямые параллельны, то ₁=₂и следовательно

k₁=k₂—условие параллельности

Если же прямые перпендикулярны, то ₁=₂/2. Поэтому

tg₂= -сtg₁ = - 1/ tg₁

или k₂ = -1/k₁, или жеk₁k₂ = -1, являютсяусловиями перпендикулярности.

Для прямых, заданных общими уравнениями

А₁х+ В₁у+ С₁= 0 и А₂х+ В₂ у+ С₂= 0

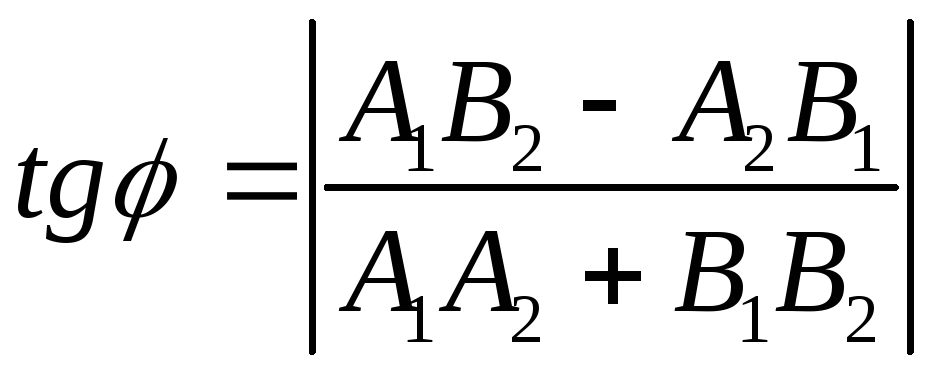
условием параллельности служит, а условием перпенди-кулярности —= 0. Эти условия нетрудно получить из условий для уравнений с угловым коэффициентом.

Уравнение прямой через заданную точку в заданном направлении. Пусть задана точка М_о(х_о, у_о) и угловой коэффициентk_o —характеризующий направление прямой. Будем искать нужное уравнение в видеу = k_o х + b. В этом направлении нам неизвестна только величинаb. Но ее можно определить из условия принадлежности к этой прямой точки М_о:у_о=k_ox_o + b, или b=у_о - k_ox_o . Подставляя это значение в уравнение найдем

у = k_o х + b=k_o х + у_о - k_ox_o = k_o (х - x_o) + у_о

или в симметричной форме

у - у_o = k_o (х - x_o).

Последнее уравнение является уравнением прямой, проходящей через заданную точку. Так как ее угловой коэффициент k_o может быть любым, то это уравнение можно трактовать как уравнение множества прямых проходящих через одну точку.

Уравнение прямой через две заданные точки. Уравнение прямой в отрезках. Пусть теперь заданы две точки М₁(х₁, у₁) и М₂(х₂,у₂). И пустьх₁  х₂иу₁  у₂. Тогда любая прямая, проходящая, например, через точку М₁описывается уравнением

у - у₁ = k (х - x₁).

Так как прямая должна проходить и через точку М₂, то ее координаты так же должны удовлетворять этому уравнению, то есть

у₂ - у₁ = k (х₂ - x₁).

Отсюда можно найти угловой коэффициент . Подставляя это значение в уравнение прямой через точку М₁, после некоторых упрощений получим уравнение прямой, проходящей через две заданные точки

.

Предположим теперь, что точка М₁лежит на оси ОХ, а точка М₂— на оси ОУ. Тогда они имеют координаты М₁(а, 0) и М₂ (0, b). Подставляя эти координаты в предыдущее уравнение, получим:

или.

Так как a и b это отрезки, отсекаемые прямой на осях координат, то последнее уравнение называют уравнением прямой в отрезках.

Расстояние от точки до прямой. Пусть прямая L задана общим уравнением Ах+ В у+ С = 0 , а точка М_о — координатами (х_о, у_о). Проведем через точку М_опрямую N, перпендикулярную L, и пусть М₁— точка пересечения L и N. Тогда расстояние от точки М_одо прямой L можно будет найти по формуле

Уравнение прямой N имеет вид:

В(х – х_о) – А(у – у_о) = 0.

Для нахождения координат точки пересечения М₁необходимо решить систему двух уравнений:

Решив эту систему относительно х₁иу₁и подставив результат в выражение дляd, получим: