
- •Дифференциальные уравнения
- •2. Дифференциальные уравнения первого порядка.
- •Понятие об изогональных траекториях.
- •7.5. Интегрирование простейших типов д.У. 1-го порядка.
- •7.5.1. Д.У. С разделяющимися переменными.
- •7.5.3. Линейные уравнения 1-го порядка.
- •7.5.5. Д.У. В полных дифференциалах.
- •3. Д.У. 2-го порядка. Интегрирование методом понижения порядка.
- •3.1. Общие положения.
- •9. Линейные д.У..
- •9.1. Введение.
- •9.2.2. Фундаментальная система решений однородного линейного д.У.
- •9.2.3. Формула Остроградского-Лиувилля Пусть и– решения (2), следовательно,
- •9.2.4. Существование фср (2)
- •9.2.5. Применение формулы Остроградского-Лиувилля
- •9.3. Линейные неоднородные дифференциальные уравнения 2-го порядка
- •9.3.1. Теоремы о частных решениях
- •9.3.2. Метод вариации произвольных постоянных для нахождения частного решения неоднородного дифференциального линейного уравнения 2-го порядка
- •9.4. Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и приводящиеся к ним
- •9.4.1. Интегрирование однородных линейных дифференциальных уравнений 2-го порядка с постоянными коэффициентами
- •9.4.2. Неоднородные линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами
- •В силу следствия достаточно найти решение уравнения
- •9.4.3. Линейные дифференциальные уравнения, приводящиеся к уравнениям с постоянными коэффициентами
- •9.4.4. Линейные дифференциальные уравнения n-го порядка
- •9.5. Системы дифференциальных уравнений
- •9.5.1. …
9. Линейные д.У..
9.1. Введение.
Линейное д.у. n-го порядка имеет вид:
(1) ![]()
где
y
– неизвестная функция аргумента x,
![]() - заданные непрерывные функции. Линейное
д.у. называется однородным, если
- заданные непрерывные функции. Линейное
д.у. называется однородным, если![]() .
.
При
![]() - уравнениенеоднородно,
или уравнение с правой частью.
- уравнениенеоднородно,
или уравнение с правой частью.
Задачу нахождения решения, отвечающего условиям:
![]() при
при
![]() называют задачей Коши для д.у.n-
называют задачей Коши для д.у.n-
го порядка.
Теорема Коши: Если в д.у. n-го порядка
![]()
функция
F
непрерывна, а ее частные производные
по
![]() ограничены
во всех точках(n+1)
– мерной области
ограничены
во всех точках(n+1)
– мерной области
![]() ,
то для любого
,
то для любого![]() существует единственное решение
существует единственное решение![]() данного д.у., удовлетворяющее начальным
условиям.
данного д.у., удовлетворяющее начальным
условиям.
![]()

Такое решение называют частным решением, соответствующим заданным начальным условиям.
Общим
решением
д.у. n-го
порядка
![]() ( определенным наD,
где выполнены условия теоремы Коши )
называют решение этого уравнения,
зависящего от n
произвольных постоянных
( определенным наD,
где выполнены условия теоремы Коши )
называют решение этого уравнения,
зависящего от n
произвольных постоянных
![]() и являющихся
совокупностью всех частных решений
данного д.у.. Существование общего
решения также гарантируется теоремой
Коши, при соблюдении ее условий.
и являющихся
совокупностью всех частных решений
данного д.у.. Существование общего
решения также гарантируется теоремой
Коши, при соблюдении ее условий.
Для
получения частного из общего необходимо
найти
![]() .
Естественно, что условия теоремы Коши
выполняются для линейного д.у.n-го
порядка в области непрерывности его
коэффициентов. Расшифровать!
.
Естественно, что условия теоремы Коши
выполняются для линейного д.у.n-го
порядка в области непрерывности его
коэффициентов. Расшифровать!
9.2. Линейные однородные д.у. 2-го порядка.
9.2.1. Теоремы о частных решениях.
Рассмотрим линейное однородное д.у. 2-го порядка :
(2) ![]()
Имеют место следующие теоремы:
Теорема
1. Всякая
линейная комбинация
![]()
![]() нескольких частных решений
нескольких частных решений![]() однородного д.у. 2-го порядка также
является его решением.
однородного д.у. 2-го порядка также
является его решением.
Доказательство: Подставляя y в (2) и группируя:
![]()
т.к
![]() теорема доказана.
теорема доказана.
В
частности сумма и разность 2-х частных
решений также является решеиями. Например
![]() - являются решениями д.у.
- являются решениями д.у.![]() ,
т.к.
,
т.к.![]() и
и![]() - решения.
- решения.
Теорема 2. Если известно одно частное решение д.у. однородного ( ненулевое ), то можно понизить порядок этого д.у. на единицу.
Док-во:
Подстановка
![]() ,
гдеz
– новая
неизвестная функция приведет к :
,
гдеz
– новая
неизвестная функция приведет к :
![]() подставляя получим:
подставляя получим:
![]()
Далее,
пусть
![]() и
и![]() и разделим все уравнение на
и разделим все уравнение на![]() тогда:
тогда:
![]() ,
где
,
где
![]() т.е. получили д.у. 1-го порядка относительноu.
т.е. получили д.у. 1-го порядка относительноu.
9.2.2. Фундаментальная система решений однородного линейного д.У.
Определение:
Ф.С.Р. однородного д.у. 2-го порядка
называется всякая пара частных решений
![]() этого уравнения, отношение которых не
равно постоянной. Такие решения также
называютлинейно-независимыми.
этого уравнения, отношение которых не
равно постоянной. Такие решения также
называютлинейно-независимыми.
Например:
![]() и
и
![]() частные решения
частные решения![]() образуют
образуют
Ф.С.Р., а
![]() и
и![]() - нет.
- нет.
Если
![]() - Ф.С.Р. то
- Ф.С.Р. то![]() - также будет Ф.С.Р.
- также будет Ф.С.Р.
Действительно,
пусть
 ,
где
,
где![]()
![]()
![]() ,
но тогда
,
но тогда ,
что и требовалось доказать.
,
что и требовалось доказать.
Таким
образом, если уравнение имеет одну ФСР,
то оно имеет их бесконечно много. Всякое
дифференциальное линейное однородное
уравнение имеет нулевое решение
![]() ,
но оно не входит ни в одну фундаментальную
систему.
,
но оно не входит ни в одну фундаментальную
систему.
Определение:
Определителем Вронского (вронскинианом)
системы двух частных решений
![]() и
и![]() уравнения (2) называют
уравнения (2) называют
 .
.
Свойства определителя Вронского:
Если
 и
и не образуют фундаментальной системы
(т.е. являются линейно зависимыми, то
их определитель Вронского тождественно
равен нулю:
не образуют фундаментальной системы
(т.е. являются линейно зависимыми, то
их определитель Вронского тождественно
равен нулю:

![]()
 .
.
Если
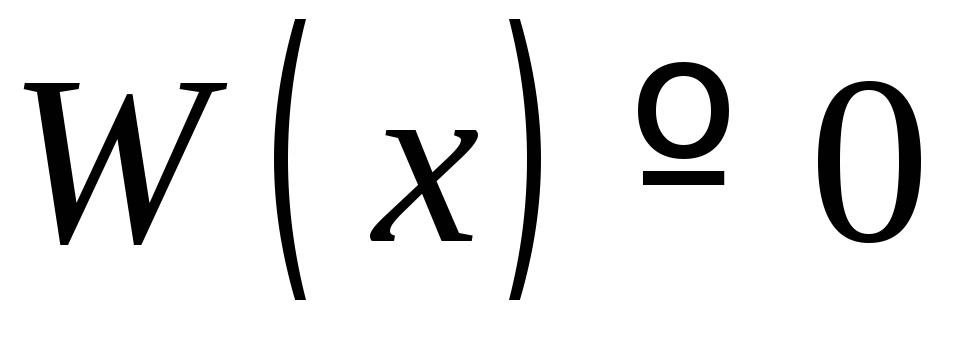 ,
то решения
,
то решения и
и – линейно зависимы.
– линейно зависимы.
Пусть
![]()
![]()
 или
или

![]()
 .
.
Если
![]()
![]()
![]()
![]()
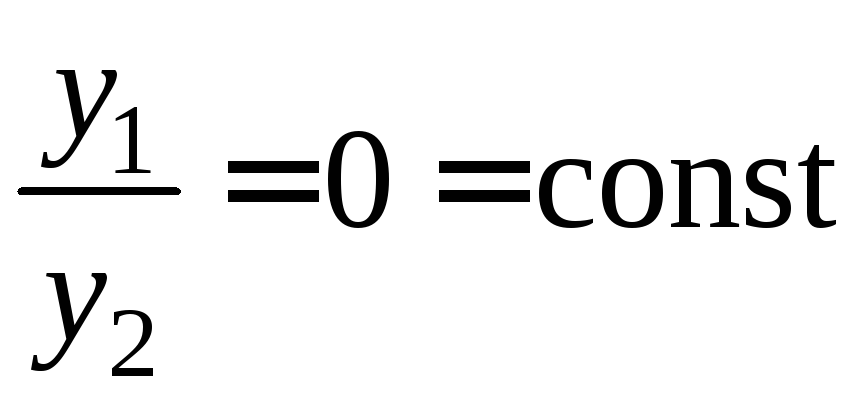 .
.
9.2.3. Формула Остроградского-Лиувилля Пусть и– решения (2), следовательно,
 .(3)
Умножим
первое из этих уравнений на
.(3)
Умножим
первое из этих уравнений на
![]() ,
а второе – на
,
а второе – на![]() и сложим их, получим
и сложим их, получим![]() , (
, (![]() )
что
равносильно
)
что
равносильно
 . (
. (![]() )
)
Это
означает, что
![]() двух решений уравнения (2) есть одно из
решений дифференциального уравнения
(1). Рассмотрим уравнение
двух решений уравнения (2) есть одно из
решений дифференциального уравнения
(1). Рассмотрим уравнение
![]() . (
. (![]() )
)
Решая его, получим:

![]()

![]()
 .
.
Поскольку
начальное условие
![]() произвольно, то и
произвольно, то и![]() является фактически произвольной
константой:
является фактически произвольной
константой:![]() .
.
Так
как определитель Вронского есть одно
из решений (![]() ),
то для него также справедлива следующая
формула:
),
то для него также справедлива следующая
формула:
 . (4)
. (4)
Формула Остроградского-Лиувилля справедлива для любых двух решений уравнения (2).
Функция
![]() непрерывна, следовательно,
непрерывна, следовательно, и справедливо следующее утверждение:
вронскиниан
и справедливо следующее утверждение:
вронскиниан![]() либо тождественно равен нулю, если
либо тождественно равен нулю, если![]() ,
либо не равен нулю ни при одном
,
либо не равен нулю ни при одном![]() ,
если
,
если![]() .
Таким образом, определитель Вронского
для фундаментальной системы решений
не только тождественно не равен нулю,
но и не обращается в ноль ни при одном
.
Таким образом, определитель Вронского
для фундаментальной системы решений
не только тождественно не равен нулю,
но и не обращается в ноль ни при одном![]() .
Существенной является непрерывность
.
Существенной является непрерывность![]() .
.
