
ЛР7_Исследование устойчивости систем регулирования во временной области и в плоскости корней характеристического уравнения
.pdf
Школа Инженерная школа энергетики НОЦ И.Н. Бутакова
Направление 13.03.01 Теплоэнергетика и теплотехника
Отчет по лабораторной работе по дисциплине «Управление техническими системами»
«Исследование устойчивости систем регулирования во временной области и в плоскости корней характеристического уравнения»
Выполнил студент |
|
|
|
гр. 5Б05 |
|
|
Цыбиков А.А. |
|
(дата, подпись) |
||
Проверил: |
|
|
|
|
к.т.н., доцент ИШЭ |
|
|
|
Атрошенко Ю.К. |
|
|
(дата, подпись) |
||
Томск 2022

Цель работы
Установить взаимосвязь между характером расположения корней характеристического уравнения и устойчивостью АСР, ее качеством
(быстродействием, степенью затухания переходных процессов).
Таблица 1 – Вариант задания
№ вар. |
N |
a0 |
a1 |
a2 |
a3 |
a4 |
|
|
|
|
|
|
|
|
2 |
57 |
431 |
4310 |
– |
– |
|
|
|
|
|
|
|
2 |
3 |
5,63 |
11,3 |
252 |
62,5 |
– |
|
|
|
|
|
|
|
|
4 |
10 |
59 |
328 |
1285 |
8790 |
|
|
|
|
|
|
|
Порядок выполнения работы
В программе МВТУ смоделировать разомкнутую систему (рис. 1).
Параметры системы взять в соответствии с таблицей исходных данных.
Рисунок 1 – Моделирование системы в программе МВТУ
Задаём параметры передаточной функции в соответствии с вариантом исходных данных:
Определяем корни характеристического уравнения.
2
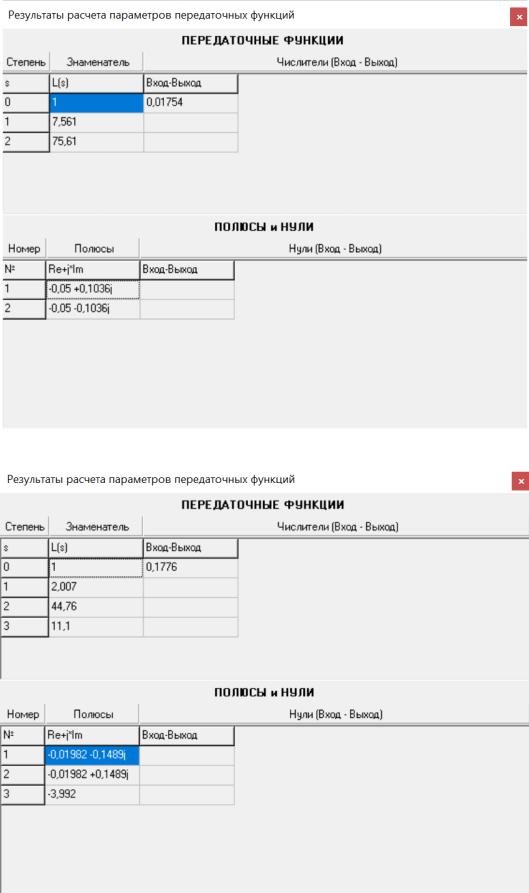
Рисунок 2 – Результат расчёта корней характеристического уравнения (N=2)
Рисунок 3 – Результат расчёта корней характеристического уравнения (N=3)
3
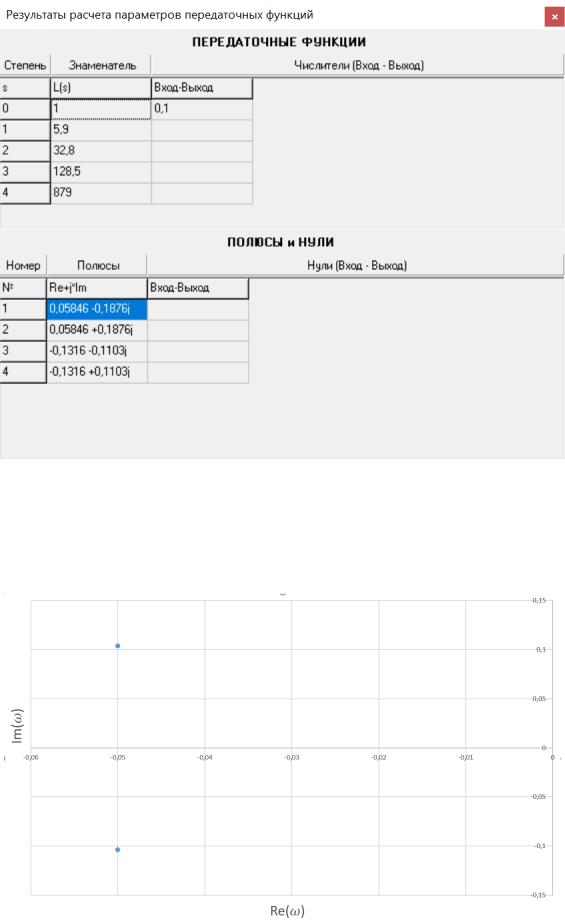
Рисунок 4 – Результат расчёта корней характеристического уравнения (N=4)
С помощью пакета MS Excel формируем картину расположения корней
на комплексной плоскости для каждой системы.
Рисунок 5 – Расположение корней полинома в программе MS Excel (N=2)
4

Рисунок 6 – Расположение корней полинома в программе MS Excel (N=3)
Рисунок 7 – Расположение корней полинома в программе MS Excel (N=4)
Для каждой системы строим график переходной характеристики и
определяем прямые оценки качества.
5

|
Рисунок 8 – График переходного процесса (N=2) |
|
||||||||||
|
По полученному графику переходной характеристики (рис. 8) определяем |
|||||||||||
прямые оценки качества: |
|
|
|
|
|
|
|
|
|
|
|
|
1) |
Динамическая ошибка: 1 = 0,003; |
|
|
|
||||||||
2) |
Перерегулирование: = |
|
1∙100% |
|
= |
0,003∙100% |
= 16,7%; |
|
||||
|
(∞) |
0,018 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||
3) |
Статическая ошибка: |
ст = − (∞) = 1 − 0,018 = 0,982, где |
– |
|||||||||
|
величина сигнала задания. |
|
|
|
|
|
|
|
|
|||
4) |
Степень затухания: Ѱ = |
|
1− 2 |
= |
|
0,003−0,018 |
= 5 |
|
||||
|
|
1 |
|
|
0,003 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
5)Время регулирования: р = 81 с.
6)Период колебаний: T = 53 с.
6

|
Рисунок 9 – График переходного процесса (N=3) |
||||||||||
|
По полученному графику переходной характеристики (рис. 9) определяем |
||||||||||
прямые оценки качества: |
|
|
|
|
|
|
|
|
|
|
|
1) |
Динамическая ошибка: 1 = 0,11; |
|
|
|
|
||||||
2) |
Перерегулирование: = |
|
1∙100% |
|
= |
0,11∙100% |
= 61,1%; |
||||
|
(∞) |
0,18 |
|
||||||||
|
|
|
|
|
|
|
|||||
3) |
Статическая ошибка: ст = − (∞) = 1 − 0,18 = 0,82, где – величина |
||||||||||
|
сигнала задания. |
|
|
|
|
|
|
|
|
|
|
4) |
Степень затухания: Ѱ = |
1− 2 |
= |
|
0,11−0,05 |
= 0,55 |
|||||
|
1 |
|
|
0,11 |
|
||||||
|
|
|
|
|
|
|
|
|
|
||
5)Время регулирования: р = 200 с.
6)Период колебаний: T = 41 с.
7

Рисунок 15 – График переходного процесса (N=4)
Т.к. переходный процесс неустойчивый определять прямые оценки
качества не нужно.
Вывод
Входе лабораторной работы были сделаны следующие выводы:
1)Переходный процесс стал неустойчивым, как только полиномы корней оказались в положительной плоскости Re( )
2)Полиномы корней находясь близко к нулю дали самый долгое время регулирования
3)Чем ближе полиномы корней находятся к нулю, тем меньше степень затухания
8
