Сопр11 / РТМ+СЕМИНАРА++5+по+ДЗ++1

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

(q, F ) = 1 ql2 EA =

.pdf

Скачиваний:

Добавлен:

10.02.2015

Размер:

429.67 Кб

Скачать

☆

РУКОВОДЯЩИЙ ТЕХНИЧЕСКИЙ МАТЕРИАЛ СЕМИНАРА ПО ДЗ № 1

Тема семинара: РАСТЯЖЕНИЕ-СЖАТИЕ статически неопределимого прямого бруса

ЗАДАЧА 1. Построение эпюр ВСФ, напряжений и перемещений в статически неопределимых соосных прямых брусьях одинаковой длины при силовом нагружении сосредоточенными силами.

1. Исходная расчетная схема

Рис. 1

РЕШЕНИЕ ЗАДАЧИ

Этап 1. Применение метода сечений к сопряжению брусьев. Выделение расчетных участков бруса.

Рис. 2 Рис. 3 Этап 2. Расчет перемещения правых концов брусьев

w1 = w1 ( R1 ) + w1 ( Р)

по числу нагрузок

Рис.4

w2 = w2 ( R2 )

Этап 3.

Расчет компонент перемещения правых концов брусьев

w =

1 3l

P l

;

(1 + 2 ) = 2

R 2l

2 EA 2 EA

Этап 4.

Статико-геометрические условия совместности деформирования брусьев

Этап 5.

R 1 + R 2 + 2 P = 0;

w1 = w2 .

Расчет реакции дополнительной

связи

R 1

+ R 2 + 2 P = 0;

R 1 + R

2 = −2 P

×2

R 1 = −

R 1

= −

R 2 = −

(

R 1

P) =

2 R 2

R 1 − 2 R 2

= −

Этап 5. Расчет функций внутренних сил

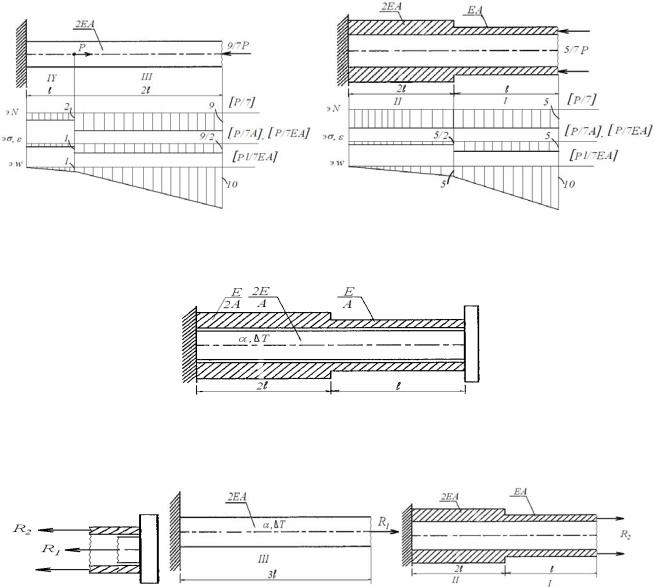
Рис. 5

Рис. 6

участок I

NI = −

5 P;

участок II

NII = −

участок III

NIII = −

участок IY

NIY == P(−

+1) = −

2 P.

Этап 6. Расчет изменений длин участков

∆lI = −

;

∆lII = −

;

7 EA

∆lIII = −

9 Pl

;

∆lIY = −

= −

7 EA

2EA

7 EA

Этап 7.

Проверка решения задачи

w 1 =

(−

−

1) = −

10 Pl

; w 2 =

(−

−

5) = −

7 EA

Этап 8.

Построение эпюр N (z),

σz (z),

εz (z), w(z)

Рис. 7 Рис. 8 ЗАДАЧА 2. Построение эпюр ВСФ, напряжений и перемещений в статически неопределимом прямом брусе при тепловом нагружении.

1. Исходная расчетная схема

Рис. 9

РЕШЕНИЕ ЗАДАЧИ

Этап 1. Применение метода сечений к опоре бруса. Выделение расчетных участков бруса.

Рис. 10 Этап 2. Расчет компонент перемещения правых концов брусьев

w =

R 1 3l

+ α 3l ∆T ;

R2 l

(1 + 2 ) = 2

R2 l

2 EA

Этап 3. Расчет реакции дополнительной связи

R 1+R 2 =0

R1 = −R 2 ;

R 1 3l

+α

3l ∆T = 2 R 2l

R 2

(2 + 3) =α 3 ∆T R 2 =

α ∆T EA

2 EA

Этап 4. Расчет функций внутренних сил

Не нужен

Этап 5.	Расчет изменений длин участков
w = α l	∆T (− 6 3 + 3) = 12 α l ∆T ;			w	2	= 2	6 α l	∆T = 12 α l ∆T .
1	7	2	7		2		7	7
Этап 6.	Построение эпюр N (z),			σz (z), εz (z),				w(z)

Рис. 11

Рис. 12

РАЗНОВИДНОСТИ ЗАДАЧ

Наименование

Расчетная схема

Этапы основных особенностей решения

Построение

Этап 1.

эпюр ВСФ в

статически

неопределимых

соосных прямых

Этап 2. δ

брусьях

= δ

( R ) + δ

(2 q ) + δ

(ql )

одинаковой

по числу нагрузок

длины при

Этап 3.

∫

(−2q x)dx −

4ql 2l

= − 6 ql

;

силовом

δ1 (2 q ) =

нагружении

2 EF

произвольными

нагрузками

Этап 5.

участок III

NIII (x) = R1 − 2qx;

Построение

Этап 1.

эпюр ВСФ в

статически

неопределимых

соосных прямых

брусьях разной

длины при

силовом

нагружении

Этап 4.

R 2 + R 3 − R 1 = 0;

δ3 = δ2 ;

δ1 = − δ2 .

Построение

Этап 3.

эпюр ВСФ в

δ2 =

2 l

+ ∆.

статически

2 E F

неопределимых

Этап 4.

соосных прямых

R 2 + R 3

− R 1 = 0;

δ3 = δ2 ;

δ1 = − δ2 .

брусьях разной

длины с зазором

при силовом

нагружении

ЗАДАЧА 3. Типовые дополнительные вопросы к использованию решения задач 1) Насколько нужно изменить температуру всего бруса, чтобы сечение М-М осталось

неподвижным, а компоненты силовой и тепловой частей суммарного перемещения даны

w	= w	(q, F ) + w (∆T ) = 1 ql2EA − 1			αl∆T = 0	∆T = 3 qlEA.
M	M	M	4	3		4 α
			4	3		4 α

2) Насколько нужно изменить температуру всего бруса, чтобы реакция левого конца бруса была равна нулю, а компоненты силовой и тепловой частей реакции левой опоры даны

R =	1 ql −	4	α ∆T EA =0	∆T =	3	ql	.
		3
	4				16 α EA

3) Найти запас по бруса текучести при силовом нагружении, если максимальное напряжение дано

= 3 ql

σT

= 8 σT A.

max

8 A

max

3 ql

4) Определить при какой нагрузке q сечение N-N переместится влево на расстояние , если податливость в точке оси бруса дана

5) Определить допустимую степень нагрева бруса при тепловом нагружении, если максимальное напряжение дано

[σ]=

σT

3[σ]

max

t =

α ∆T E =[σ]

∆T =

4α E

6) Найти запас бруса по текучести при тепловом нагружении, если максимальное напряжение дано

t = 4

α ∆T E

n =

σT

= 3

σT

max

α ∆T E

7)Определить при каком изменении температуры сечение N-N переместится влево на

расстояние , если податливость в точке N оси бруса дана

8) Найти работу внешних сосредоточенных сил, если сила и перемещение точки ее приложения

даны

A(ql) = ql wN = 1 q2l3 . 4 EA

9) Найти изменение потенциальной энергии при силовом нагружении бруса, если функции усилий и жесткости участков даны

участок I

∆П I =

q 2 l 2 l

d z

1 q 2 l 3

;

∫

1 6

3 2 E A

2 E A 0

участок II

∆П II

q 2 l 2

9 d z

9 q 2 l

;

∫

2 E A

1 6

6 4 E A

∆П =

1 ∫ N

( z ) d z

участок III

∆П III =

∫ ( −

3 q l + q z ) 2 d z =

2 0

E A

2 2 E A

q 2 l 3

(

−

) =

q 2 l 3 2 7 −

3 6 + 1 6

7 q 2 l 3

;

4 E A

1 6

4 E A

1 6 3

1 9 2 E A

2 l

d z

1 q 2 l 3

участок IY

∆П IY

∫

1 6

3 2 E A

2 E A 0

∆П =

q 2 l 3

) =

q 2 l 3 6 +

2 7 +

7 +

2 3 q 2 l 3

(

E A

3 2

6 4

1 9 2

3 2

E A

1 9 2

9 6 E A

10) УКАЗАНИЕ: в задачах с зазором алгоритм никак не изменяется и лишь на этапе 4 перемещение правого торца равно заданному зазору , а в эпюрах перемещений в сечении с зазором будет разрыв эпюры перемещений на заданную величину зазора .

ЗАДАНИЕ К СЕМИНАРУ ПО ДЗ № 2

Выполнить В ТЕЧЕНИЕ НЕДЕЛИ ПОСЛЕ ВЫДАЧИ РТМ задачу представленного типа и представить на контроль ЧЕРЕЗ НЕДЕЛЮ ПОСЛЕ ВЫДАЧИ РТМ.

Отчет подготовить на бумаге формата А4

Соседние файлы в папке Сопр11

#
10.02.2015269.74 Кб21РТМ+2+ДЗ+1.pdf
#
10.02.2015273.82 Кб22РТМ+3+ДЗ+1.pdf
#
10.02.2015293.36 Кб21РТМ+СЕМИНАРА+++2-ДЗ3.pdf
#
10.02.2015202.17 Кб23РТМ+СЕМИНАРА+++3-1.pdf
#
10.02.2015189.46 Кб21РТМ+семинара++4+-+ДЗ++3.pdf
#
10.02.2015429.67 Кб22РТМ+СЕМИНАРА++5+по+ДЗ++1.pdf
#
10.02.2015217.2 Кб22РТМ+семинара++З+-+ДЗ3.pdf
#
10.02.201577.82 Кб21Шарнирно-стержневые+системы+-+еди.doc