
Сопр11 / РТМ+СЕМИНАРА+++2-ДЗ3
.pdf
РУКОВОДЯЩИЙ ТЕХНИЧЕСКИЙ МАТЕРИАЛ СЕМИНАРА ПО ДЗ № 3
Тема семинара: ПРОЕКТИРОВОЧНЫЙ РАСЧЕТ БАЛКИ НА ПРОЧНОСТЬ
ЗАДАЧА. Определить допускаемую нагрузку статически определимой балки постоянного сечения, нагруженной произвольной системой сил.
1. Исходная расчетная схема
Рис. 1 2. Исходные формы сечения балки из упруго-пластичного материала.
Рис. 2
3. Исходная форма сечения балки из пластичного материала.
Ритс. 3
РЕШЕНИЕ ЗАДАЧИ
Этап 1. Расчет геометрических характеристик сечения, составленного из прямоугольников. 1.1. Расчет положений центров тяжести частей сечения во вспомогательной системе координат x-yc . (При этом вводятся оси x1, x2, x3 , проходящие через центры тяжести частей сечения.)

Рис. 5
1.2. Геометрические характеристики частей сечения
Примечание. В случае симметричного относительно оси yc сечения определяются геометрические характеристики правой половины сечения, в противном случае – всего сечения.
Площади частей правой половины поперечного сечения
F{1} = 2 b2 ; |
F{2} =14 b2 ; |
F{3} = 2b2 . |
||||
Координаты yc |
центров тяжести частей правой половины сечения |
|||||
yc{1} = b; |
yc{2} = |
|
7 |
b; |
yc{3} = 5b. |
|
2 |
||||||
|
|
|
|
|||
Моменты инерции частей 1, 2, 3 правой половины сечения относительно
осей соответственно x1 , x2 , |
x3 |
|
|
|
|
|
|
|
|
|||||||
Ix{1} = |
b(2b)3 |
= |
|
8 |
b4 ; |
Ix{2} = |
2b(7b)3 |
= |
686 |
b4 |
; |
Ix{3} = |
|
8 |
b4 . |
|
12 |
12 |
12 |
12 |
12 |
||||||||||||
1 |
|
|
2 |
|
|
|
3 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1.3. Статические моменты частей правой половины сечения
Sx{1} = F {1}yc{1} = 2b3 ; Sx{2} = F {2}yc{2} = 49b3 ; Sx{3} = F {3}yc{3} =10b3 .
1.4. Координата центра тяжести всего сечения во вспомогательной системе координат x-yc
y = |
S |
x |
= |
2(S{2} −S{}1 |
−S{3}) |
= |
37 |
b. |
|
|
x |
x |
x |
|
|||||
|
|
2(F{2} −F{}1 −F{3}) |
10 |
||||||
c |
F |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
1.5. Расчет момента инерции сечения во вспомогательной системе координат.
(Используется теорема Штейнера |
I |
x |
= I |
x |
+ F y2 ) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
I |
{1} |
= I{1} |
+F{1} y{1}2 |
=b4 ( |
8 |
|
+2) = |
32 |
b4 ; |
|
|
|
|
|
|
|
|
|
|
|||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x |
|
c |
12 |
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I{2} = I{2} +F{2} y{2}2 =b4 ( |
686 |
+14 |
49 |
) = |
2744 |
b4 ; |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
x |
x |
|
c |
12 |
|
4 |
|
|
|
|
|
12 |
|
|
|
|
|
||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
{3} |
= I{3} |
+F{3} |
y{3}2 |
=b4 ( |
8 |
|
+2 |
25) = |
608 |
b4 ; |
|
|
|
|
|
||||||||||||||
x |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
x |
|
c |
12 |
|
|
12 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ix =2(Ix{2} −Ix{}1 |
−Ix{2}) =2b4 ( |
2744 |
− |
32 |
− |
608 |
) = |
1052 |
b4. |
|
||||||||||||||||||||
12 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
12 |
|
|
|
|
3 |
|
|
|||||||||
1.6. Расчет главного центрального момента инерции сечения, координат точек, наиболее удаленных от центра тяжести сечения при рациональном расположении сечения для [σ]P>[σ]C
Из теоремы Штейнера следует

I xc |
= I x − F yc2 |
= b4 ( |
1052 |
− 20 |
|
1369 |
) = |
|
1153 |
b4 |
= 76.9b4 |
; |
||||||||
|
100 |
15 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||||
Определение допускаемых напряжений на растяжение и сжатие |
|
|||||||||||||||||||
[σ ] |
|
= |
σ ò ,ð |
; |
[σ |
] = |
σ ò ,ñ |
; |
|
|
|
|
|
|
||||||
p |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
n ò ,ð |
|
|
c |
|
n ò ,ñ |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
[σ] |
p |
> |
[σ] ; |
yp,max > yc,max |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
yp,max =3,7b; |
yñ,max =3,3b. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
Этап 2. Расчет допускаемой нагрузки балки из пластичного материала по условию прочности
Прямоугольное сечение
σ |
z ,m ax |
= |
|
|
M x |
|
m ax |
= |
|
|
M x |
|
m ax |
= |
ql 2 |
≤ [σ ]; q ≤ |
0.375b 3 [σ ] |
= |
|
= [ |
Í |
|
]. |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
W x |
0.375b 3 |
|
0.375b 3 |
|
l 2 |
|
… |
|
Ì |
Ì |
|
||||||||
Этап 3. Расчет допускаемой нагрузки балки из пластичного материала по условию прочности для комбинированного сечения.
3.1. Обеспечение прочности при растяжении
|
|
|
|
|
|
|
M x |
|
max |
|
|
|
|
|
|
76.9b4 [σ ]ð |
|
|
Í |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
σz , ð ,max |
= |
|
|
|
|
|
|
|
|
|
y ð ,max ≤ [σ ]p |
; |
|
q ð ≤ |
|
= |
|
= [ |
|
]. |
||||||
I xc |
l 2 y ð ,max |
… |
Ì Ì |
|||||||||||||||||||||||
3.2. Обеспечение прочности при сжатии |
|
|
|
|
|
|
|
|||||||||||||||||||
|
σz,ñ |
|
= |
|
|
|
Mx |
|
max |
yñ,max ≤[σ] ; |
|
qñ |
≤ |
76.9b4 [σ]c |
= |
=[ |
Í |
]. |
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
Ì Ì |
|
|
|||||||||||||||
|
|
max |
|
|
|
|
Ixc |
ñ |
|
|
|
l |
2 |
yc,max |
… |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3.3. Обеспечение прочности по допускаемым нагрузкам всего сечения как при сжатии, так и при растяжении
q =min(qp ,qñ ) = ìÍì .
ЗАДАНИЕ К СЕМИНАРУ ПО ДЗ №3
Выполнить В ТЕЧЕНИЕ НЕДЕЛИ ПОСЛЕ ВЫДАЧИ РТМ выполнить расчеты ДЛЯ ЗАДАННОЙ БАЛКИ и представить на контроль ЧЕРЕЗ НЕДЕЛЮ ПОСЛЕ ВЫДАЧИ РТМ . Отчет подготовить на бумаге формата А4 с титульным листом по образцу.
ДОПОЛНЕНИЕ. I часть
Этап 3. Расчет параметров форм сечений из упруго-пластичного материала из условия прочности
Прямоугольное сечение
σ z ,m ax = |
|
M x |
|
m ax |
= |
|
M x |
|
m ax |
≤ [σ ]; |
|
b ≥ 3 |
|
M x |
|
m ax |
= 3 |
|
= [M M ]. |
|
|
|
|
|
|
||||||||||||||
|
W x |
0.375b 3 |
0.375 [σ ] |
|
|||||||||||||||
Этап 4. Расчет параметров форм сечений из упруго-пластичного материала.
4.1. Обеспечение прочности при растяжении
σz , ð ,max |
= |
|
M x |
|
max |
y ð ,max |
≤ [σ ]p |
; |
|
bp |
≥ 3 |
3.7 |
M x |
max |
= 3 |
|
= [MM ]. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
76.9 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
I xc |
|
|
|
|
|
|
|
|
[σ ]p |
|
|
|
|
|||||||||||||
4.2. Обеспечение прочности при сжатии |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
σz,ñ |
|
= |
|
Mx |
|
max |
yñ,max |
≤[σ] ; |
|
bñ |
≥ 3 |
3.3 |
|
Mx |
|
max |
= 3 |
|
=[MM ]. |
|||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
max |
|
Ix |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ñ |
|
|
|
76.9[σ] |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|||||
4.3. Обеспечение прочности всего сечения как при сжатии, так и при растяжении
b =max(bp ,bс) = [MM ].
____________________________________________________________________________
II часть
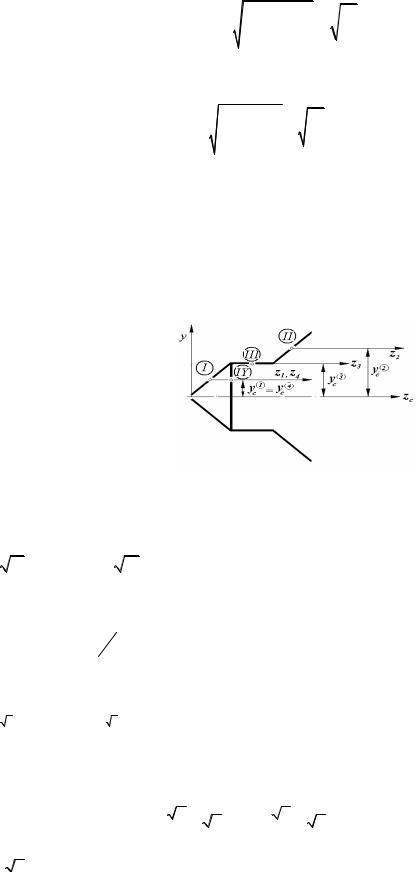
Этап 2. Расчет геометрических характеристик тонкостенного сечения
Рис. 4
2.1. Площади элементов сечения
F{1} = 2 δ b ; F{2} = 2 δ b ; F{3} = δ b ; F{4} = δ b;
2.2. Координаты центров тяжести элементов сечения во вспомогательной системе координат
y{1} = b / 2; |
y{2} = 3 |
2 |
b; |
y{3} = b; |
y{4} = b / 2; |
c |
c |
|
c |
c |
2.3. Моменты инерции элементов сечения относительно центральных осей этих элементов
{1} |
|
2δ b3 |
{2} |
|
2δ b3 |
{3} |
|
{4} |
|
δ b3 |
|
Iz1 |
= |
|
; Iz2 |
= |
|
; Iz3 |
=0 ; |
Iz4 |
= |
12 |
; |
12 |
12 |
2.4. Геометрические характеристики сечения для расчетов на прочность и жесткость
|
|
|
|
{i} |
|
{i} {i}2 |
|
|
|
|
1 |
2 |
|
2 |
|
3 |
2 |
|
|
1 |
|
1 |
2 |
|
|||||
|
|
4 |
|
3 2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
I zc = ∑ ( I zi |
+ F y zi ) =2 δb |
|
+ 2 |
|
|
|
+ |
|
+ 2 |
|
|
|
+ 1 |
+ |
|
|
+ |
|
|
|
; |
||||||||
1 2 |
|
|
1 2 |
|
|
1 2 |
|
|
|||||||||||||||||||||
|
|
|
i =1 |
|
|
|
|
|
|
2 |
|
|
|
2 |
|
i =3 |
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
i =1 |
|
|
|
i =2 |
|
|
|
|
|
|
|
i =4 |
|
|
|
|
|||
I zc |
= |
|
1 6 2 + 8 |
δb 3 = 1 .0 2 1b 4 ; |
W z = |
|
I zc |
= 0 .5 0 1b 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 b |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.6. Расчет главного центрального момента инерции сечения, координат точек, наиболее удаленных от центра тяжести сечения при рациональном расположении сечения для [σ]P>[σ]C

I |
|
=I |
|
−F y2 |
=b4 ( |
1052 |
−20 |
1369 |
) = |
1153 |
b4 =76.9b4; |
|||
zc |
z |
|
|
|
||||||||||
|
|
|
|
|
c |
3 |
|
100 |
15 |
|
||||
[σ] |
|
|
|
[σ] |
|
|
|
|||||||
p |
> |
yp,max > yc,max |
|
|
|
|
||||||||
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
yp,max =3,7b; |
yñ,max =3,3b. |
|
|
|
|
|||||||||
Этап 3. Расчет параметров форм сечений из пластичного материала
3.2. Двутавровое сечение
σ z ,max = |
|
|
M x |
|
|
|
|
|
≤ [σ ]; |
|
W x ≥ |
|
|
M x |
|
|
|
= |
|
= M M |
; |
|||||||||
|
|
|
|
|
|
|
|
|
m ax |
|
|
|
|
|
|
|
|
|
|
|
|
max |
|
|
|
|
3 |
|||
|
|
|
|
|
|
W x |
|
|
|
|
|
|
|
|
|
|
|
|
|
[σ ] |
|
|
|
|
|
|||||
ГОСТ |
|
|
|
|
|
|
W x ,факт ≥ W x |
|
профиль № . |
|
||||||||||||||||||||
3.3. Тонкостенное сечение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
M x |
|
max |
|
|
|
|
M x |
|
max |
|
|
|
|
|
|
M x |
|
max |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
σ z ,max = |
|
Wx |
|
= |
|
0.501b3 |
≤ [σ ]; |
|
b ≥ |
3 |
0.501[σ |
] |
= |
3 |
= [MM ]. |
|
||||||||||||||
Этап 4. Расчет параметров форм сечений из пластичного материала
4.1. Прямоугольное сечение
σ z ,m ax = |
|
M x |
|
m ax |
|
= |
|
|
M x |
|
m ax |
|
≤ [σ ]; |
|
|
b ≥ 3 |
|
|
M x |
|
m ax |
|
= 3 |
|
= [M M ]. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
W x |
|
|
|
|
0.375b 3 |
|
|
|
0.375 [σ ] |
|
|
|||||||||||||||||||||||||||||||||
4.2. Двутавровое сечение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
σ z , m a x = |
|
|
M x |
|
m a x |
≤ [σ ]; |
|
W x |
≥ |
|
|
|
M |
x |
|
|
m a x |
|
|
= |
|
|
= |
|
M M 3 |
; |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[σ ] |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
W x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Г О С Т |
|
|
|
|
|
|
W x , ф а к т ≥ W x |
|
п р о ф и л ь № . |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
4.3. Тонкостенное сечение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
M x |
|
max |
|
|
|
M x |
|
max |
|
|
|
|
|
|
|
|
M x |
|
max |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
σ z ,max = |
|
|
Wx |
|
= |
0.501b3 |
≤ [σ ]; |
b |
≥ |
3 |
0.501[σ |
] |
|
= |
3 |
|
= [MM |
]. |
|
|
||||||||||||||||||||||||||||
Этап 5. Расчет параметров форм сечений из композиционного материала.
5.1. Обеспечение прочности при растяжении
σz , ð ,max |
= |
|
M x |
|
max |
y ð ,max |
≤ [σ ]p |
; |
|
bp |
≥ 3 |
3.7 |
M x |
max |
= 3 |
|
= [MM ]. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
76.9 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
I xc |
|
|
|
|
|
|
|
|
[σ ]p |
|
|
|
|
|||||||||||||
5.2. Обеспечение прочности при сжатии |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
σz,ñ |
|
= |
|
Mx |
|
max |
yñ,max |
≤[σ] ; |
|
bñ |
≥ 3 |
3.3 |
|
Mx |
|
max |
= 3 |
|
=[MM ]. |
|||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
max |
|
Ix |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ñ |
|
|
|
76.9[σ] |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|||||
5.3. Обеспечение прочности всего сечения как при сжатии, так и при растяжении
b =max(bp ,bс) = [MM ].
Этап 6. Сравнить площади рассчитанных сечений и изобразить все сечения в едином масштабе для сравнения.
