
Сопр11 / Основные+определения+ДЗ+1++РТМ+++ПЛ
.pdf
I. Основные определения для идентификации расчетных схем задания
Понятие |
Определение понятия |
Иллюстрация понятия |
|
|||
|
Тело, одно из измерений |
|
|
|
||
Брус |
которого (длина) намного |
|
|
|
||
|
(>10 раз) превышает другие |
|
|
|
||
|
измерения |
|
|
|
||
|
|
|
|
|
|
|
|
Линия, проходящая через |
|
|
|
||
Ось бруса |
центр тяжести сечений |
|
|
|
||
|
бруса. Отображает форму |
|
|
|
||
|
бруса в расчетных схемах. |
|
|
|
||
|
|
|
|
|
|
|
|
Ось бруса - прямая. |
|
|
|
||
|
Нагрузки: |
|
|
|
||
Прямой |
|
1) Силы по оси бруса |
|
|
|
|
брус |
|
( растяжение-сжатие) |
|
|
|
|
|
|
2) Пары сил в плоскости, |
|
|
|
|
|
|
оси бруса( кручение ) |
|
|
|
|
|
|
|
|
|
|
|
|
Прямой брус, нагруженный |
|
|
|
||
Балка |
силами, оси, и парами сил |
|
|
|
||
в плоскости. образованной |
|
|
|
|||
|
осью бруса и осью, оси. |
|
|
|
||
Опоры бруса |
|
|
|
|
|
|
|
|
|
|
|
или |
жесткое |
|
|
|
|
|
защемление (заделка) |
|
Стержень |
Брус с любой формой оси |
, нагруженный нагрузками любого направления |
||||
Стержневая |
Совокупность стержней, объединенных в единую конструкцию |
|
||||
система (СС) |
с помощью любых связей |
|
|
|
||
Растяжение |
Удлинение оси бруса |
Сжатие Укорочение оси бруса |
|
|||
Кручение |
|
Поворот сечений бруса вокруг |
его оси (кривизна оси бруса неизменна) |
|
||
Изгиб |
|
Поворот сечений бруса вокруг оси, оси бруса (кривизна оси бруса изменяется) |
||||
|
|
СС, все элементы которой |
|
|
|
|
Рама |
|
испытывают изгиб |
|
|
|
|
|
|
|
|
|
|
|
Плоская рама |
Рама, все стержни которой имеют оси, лежащие в одной плоскости, |
|
|
и нагрузки действуют также в этой плоскости |
|
Плоско-прост |
Брус, ось которого лежит в плоскости, не совпадающей с плоскостью действия |
|
ранственный |
нагрузок |
|
брус |
|
|
Плоско-прост |
Рама, элементами которой |
|
ранственная |
являются только |
|
рама |
плоскопространственные |
|
|
брусья |
|
|
|
|
Пространствен |
Брус, ось которого является пространственной линией |
|
ный брус |
|
|
Пространствен |
Рама, оси элементов которой |
|
ная рама |
образуют пространственную |
|
|
линию |
|
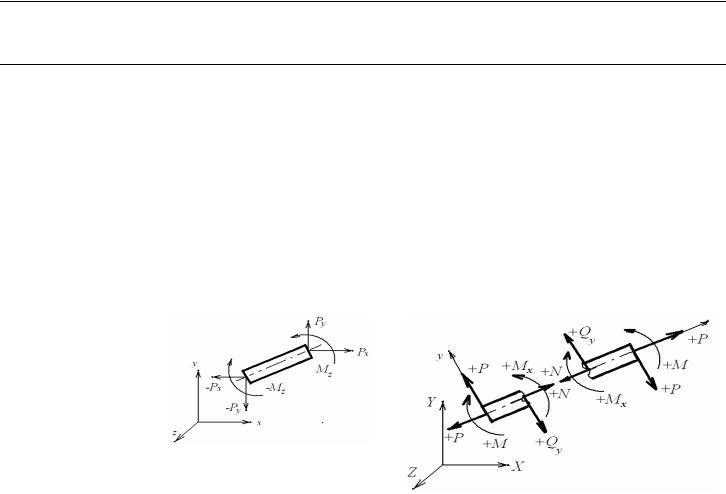
II. Основные определения для идентификации внутренних силовых факторов (ВСФ)
Понятие |
|
Содержание понятия |
|||
|
|
|
|
||
|
|
Теоретическая механика |
Сопротивление материалов |
||
|
|
|
|
||
|
|
Результат приведения всех |
Результат приведения всех внешних сил, |
||
r |
|
внешних сил, действующих на |
действующих на ОТСЕЧЕННУЮ ЧАСТЬ |
||
Главный вектор R |
|
тело, к избранному полюсу |
тела к ЦЕНТРУ ТЯЖЕСТИ СЕЧЕНИЯ |
||
|
|
|
БРУСА |
||
|
|
|
|
||
|
|
Результат приведения |
Результат приведения МОМЕНТОВ всех |
||
r |
|
МОМЕНТОВ всех внешних сил |
внешних сил и ПАР СИЛ, действующих на |
||
Главный момент M |
и ПАР СИЛ, действующих на |
ОТСЕЧЕННУЮ ЧАСТЬ тела к ЦЕНТРУ |
|||
|
|
тело, к избранному полюсу |
ТЯЖЕСТИ СЕЧЕНИЯ БРУСА |
||
|
|
|
|||
Оси, используемые |
Оси ГЛОБАЛЬНОЙ |
Оси локальной системы координат, |
|||
при расчете главных |
ДЕКАРТОВОЙ |
образуемой в центре тяжести избранного |
|||
вектора Rr и |
|
системы координат (СК) для |
сечения бруса. Ориентация осей триедра |
||
r |
|
зависит от геометрии оси бруса, |
|||
|
всей конструкции |
||||
момента M |
|
исследуемого в составе конструкции. |
|||
|
|
|
|||
Компоненты |
|
r |
R N, Qy , Qx |
||
главного вектора Rr |
R Rx , Ry , Rz |
||||
Компоненты |
|
r |
|
|
|
r |
M M x , M y , M z |
M M k , M y , M x |
|||
|
|||||
главного моментаM |
|
|
|
||
|
|
|
|
||
|
|
|
N растяжение/сжатие бруса |
||
Связь компонент |
|
НЕТ никакой связи, так как все |
Q y |
, Q x сдвиг (срез) сечения бруса |
|
главных вектора и |
|
элементы конструкции без |
M k |
|
|
момента с деформи- |
исключения считаются |
кручение бруса |
|||
рованием бруса |
|
абсолютно жесткими |
M y , M x изгиб бруса |
||
|
|
|
|||
|
|
|
|
||
Правила положи- |
|
Связаны с ОСЯМИ декартовой СК |
Связаны с СЕЧЕНИЯМИ бруса |
||
тельных знаков при |
|
|
|
||
расчете компонент |
|
|
|
||
главных вектора и |
|
|
|
|
|
момента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N , |
Q y , Q x - внутренние силы |
|
Внутренний силовой |
НЕ ИМЕЕТ ПРАВА НА |
M k |
, M y , M x - моменты внутренних сил |
||
фактор |
|
СУЩЕСТВОВАНИЕ, так как |
относительно главных центральных осей |
||
|
|
все элементы конструкции |
рассматриваемого сечения бруса и оси бруса |
||
|
|
считаются абсолютно жесткими |
(триедр осей) |
||
|
|
|
|
|
|

III.Основные определения для анализа внутренних силовых факторов (ВСФ)
Понятие |
Использование понятия |
|
|
|
|
|
Комментарий |
|
|
При однократном использовании МС для |
|
|
|
Метод сечения является |
|||
|
|
|
|
наиболее универсальным |
||||
|
выбранного или заданного сечения необходимо: |
|
методом выявления и |
|||||
|
1) Разрезать мысленно брус на две части |
|
|
расчета внутренних сил в |
||||
Метод сечений(МС) |
2) Отбросить одну из частей (обычно с опорой |
|
любом деформируемом |
|||||
(основной метод, |
бруса) |
|
|
|
|
|
теле, но при нагружении |
|
алгебраический |
3) Заменить действие отброшенной части |
|
|
произвольными |
||||
метод расчета ВСФ) |
соответствующими силами действия |
|
|
нагрузками приводит |
||||
|
отброшенной части на отсеченную |
|
|
|
иногда к относительно |
|||
|
4) Уравновесить осеченную часть бруса |
|
|
более трудоемким |
||||
|
согласно положениям статики теоретической |
|
арифметическим |
|||||
|
механики |
|
|
|
|
|
вычислениям |
|
|
Используется в форме, имеющей конкретный вид и |
|
|
|||||
|
смысл |
|
|
|
|
|
|
Обобщение понимается в |
Обобщенный |
1) |
Растяжение/ сжатие |
→ продольнаясилаN |
|
смысле использования |
|||
внутренний силовой |
2) |
Сдвиг(срез)/изгиб |
→поперечныесилыQ ,Q |
|
ВСФ в энергетическом |
|||
фактор R |
|
|
|
|
y |
x |
|
подходе и единой |
: R |
Кручение →крутящиймоментMk |
|
|
|
||||
|
3) |
|
|
|
структурной методики |
|||
|
4) Изгиб →изгибающиемоментыM , M |
|
|
расчета ВСФ |
||||
|
|
|
|
y x |
|
|
|
|
Дифференциальный |
Записать универсальное дифференциальное уравне- |
|
Обычно ДУ для криволи- |
|||||
метод (дополнительние (ДУ) равновесия обобщенного ВСФ на беско- |
|
нейного бруса не |
||||||
ный метод расчета |
нечно малом участке прямого бруса |
dR |
= q ( z ) |
, |
|
используется ради |
||
ВСФ) |
|
|
|
dz |
|
упрощения расчетов |
||
|
|
|
|
|
|
|||
q(z) – соответствующая R распределенная нагрузка.
|
МНП используется при представлении общего |
|
||
|
решения неоднородного ДУ в форме интеграла с |
МНП – универсальный |
||
|
переменным верхним пределом |
метод нахождения общего |
||
|
|
z |
решения любого ДУ с |
|
Метод начальных |
|
R ( z ) = R ( 0 ) + ∫ q (ξ ) d ξ . |
одновременным выделе- |
|
|
0 |
|
||
параметров (МНП) |
R(0) – начальный параметр - ВСФ в начале расчетного |
нием произвольной |
||
|
|
z |
постоянной в форме |
|
|
участка (ξ=0), ∫q (ξ ) d ξ обычно вычисляется на |
|||
|
дискретного значения |
|||
|
|
0 |
|
|
|
основании геометрического смысла определенного |
искомого решения |
||
|
интеграла (то есть по площади подынтегральной |
|
||
|
функции при ξ[0,z]. |
|
||
|
Используется для представления функции одной |
Чаще всего используют не |
||
|
переменной в виде единого графика независимо от |
эпюры ВСФ, а совокуп- |
||
Эпюра |
ее особенностей с точки зрения математического |
ность эпюр, описываю- |
||
|
анализа |
щих состояние бруса |
||
Особенности эпюр |
Разрыв первого рода в сечении с внешней сосредо- |
|
Разрыв равен величине |
|
ВСФ |
точенной обобщенной нагрузкой |
нагрузки |
||
Расчетное сечение |
Вводится в сечении с приложенной внешней сосре- |
|
Позволяет выделить сече- |
|
бруса |
доточенной обобщенной нагрузкой или в сечении |
ния бруса для расчета |
||
|
разрыва функции распределенной нагрузки q(z) |
значения ВСФ R(0) |
||
Расчетный участок |
Вводится между двумя соседними расчетными |
|
Позволяет использовать |
|
бруса |
сечениями бруса |
локально аналитические |
||
|
|
|
|
функции ВСФ |
|
Для прямого бруса: |
|
Позволяют без ошибки |
|
|
1) Ось эпюры под осью бруса и параллельна ей |
определить знак произ- |
||
|
2) |
Ординаты эпюр должны быть безразмерны |
ведения любых эпюр в |
|
Правила построения |
3) |
Положительные ординаты откладываются вверх, |
интеграле Мора всего |
|
эпюр ВСФ для бруса |
|
отрицательные вниз БЕЗ простановки знака |
лишь по внешнему виду |
|
|
Для криволинейного бруса эпюры строятся на но- |
эпюр для бруса любой |
||
|
вом представлении геометрии с описанием функций |
геометрии |
||

IY. Методика расчета ВСФ статически определимого бруса
Этап |
|
Действия |
|
Иллюстрация действия |
||
|
|
|
|
|
|
|
Выделение расчетных |
|
|
|
|
|
|
сечений и участков бруса |
1. Выделение расчетных сечений бруса |
|||||
|
||||||
|
2. Выделение расчетных участков бруса |
|||||
|
|
|
|
|
||
|
∑Ri =0 N |
|
|
|
||
|
ОТС |
|
|
|
|
|
Построение эпюры |
1.Участок I : NI |
= −2ql |
|
|
||
обобщенных ВСФ на |
2.Участок II: NII |
= ql(−2 +3) = ql |
||||
одном участке бруса с |
||||||
использованием только |
3.Участок III: |
|
|
|
|
|
метода сечений |
|
|
|
|
||
|
NIII (z) = ql(−2 +3) −qz = ql −qz |
|||||
|
|
|
|
|
||
|
|
|
|
z |
||
|
Ni(z) =Ni(0) +∆Ni(z); |
∆Ni(z) = |
∫qi(ξ)dξ . |
|||
|
|
|
|
014243 |
|
|
|
|
|
|
площадь |
||
|
|
|
|
подынтегральной |
||
Построение эпюры |
1.Участок I : |
|
|
функции |
||
обобщенных ВСФ на |
|
|
|
|
||
одном участке бруса с |
NI (0) = −2ql; ∆NI = 0; |
NI = NI (0). |
||||
использованием метода |
||||||
14243 |
|
|
|
|||
сечений и МНП |
|
|
|
|
|
|
2.Участок II:
NII (0) =ql(−2+3) =ql; ∆NII =0; NII =NII (0).
14243
3.Участок III:
NIII (0) = NII = ql; ∆NIiI (x) = −qx; NII = ql − qx.
Рекуррентное построение |
N (0) |
=−2ql; |
N |
=N (0), |
|
эпюры обобщенных ВСФ в |
I |
|
I |
I |
|
N (0) |
=ql; |
N |
=N (0), |
||
брусе с использованием |
II |
|
II |
II |
|
NIII (0) =ql; ∆NIII (x) |
=−qz; NIII (x) =ql −qz. |
||||
комбинации метода |
|||||
сечений и МНП |
|
|
|
|
|

РУКОДЯЩИЙ ТЕХНИЧЕСКИЙ МАТЕРИАЛ СЕМИНАРА ПО ДЗ № 1
Тема семинара: РАСТЯЖЕНИЕ-СЖАТИЕ статически неопределимого прямого бруса
ЗАДАЧА 1. Построение эпюр ВСФ в статически определимом прямом брусе при силовом нагружении произвольными нагрузками.
1. Исходная расчетная схема
Рис. 1
РЕШЕНИЕ ЗАДАЧИ
Этап 1. Выделение расчетных участков бруса.
Рис. 2 Этап 2. Расчет продольных сил в расчетных сечениях
сечение |
5 |
: |
N5 |
= 1 ql; |
|
|
|
|
|
|
|
сечение |
|
4 |
: |
|
N4 |
(+0) = 1 ql; |
|
|
N4 (−0) = ql( |
1 |
−1) |
= − |
3 ql; |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|||
сечение |
3 |
: |
N |
3 |
= − 3 ql; |
|
сечение 2 : |
|
|
N |
2 |
= ql( 1 |
−1 +1) = 1 ql; |
|
сечение 1 |
: N |
|
= ql( 1 −1 +1) = 1 ql. |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
4 |
|
|
|
4 |
|
|||||
Этап 3. Расчет функций внутренних сил |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
участок IY |
: |
N IY = |
1 ql; |
|
|
|
|
|
|
|
|
участок III : |
|
|
|
N III |
= − |
|
3 ql; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
участок II |
: |
N II (x) = − 3 ql + qz; |
|
|
|
участок I |
: |
|
N IY |
= |
1 ql. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Этап 4. Расчет функций напряжений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
участок IY |
: |
σz, IY = |
1 ql |
|
; |
|
|
|
|
|
|
участок III |
: |
|
|
σz,III |
= − |
|
3 ql |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
участок II |
: |
σz,II ( x) = |
q |
|
(− |
3 l + |
z |
); |
|
участок I |
: |
|
|
σz,I |
= |
|
1 ql . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
A |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Этап 5. Расчет изменений длин расчетных участков |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
участок I |
: ∆lI = |
|
1 ql2 |
; |
|
|
|
|
|
|
участок II |
|
|
: |
|
|
∆lII |
= |
|
l |
N |
II |
(z)dz |
= |
|
|
1 l |
(− |
3 |
ql +qz)dz = |
ql2 |
|
(− |
3 |
+ |
1 |
|
1 |
) =− |
1 ql2 |
; |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
4 EA |
|
|
|
|
|
|
|
|
|
|
|
|
2EA |
|
|
|
|
4 |
EA |
8 |
2 |
2 |
8 EA |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
2EA 0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
участок III |
: |
∆lIII |
=− |
3 ql2 |
|
; |
|
|
участок IY |
|
|
: |
|
|
∆lIY |
= |
1 ql2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
8 EA |
|
|
|
|
|
|
4 EA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Этап 6. Расчет перемещений расчетных сечений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
δ2 = ∆lI = |
1 q l |
2 |
|
δ3 = ∆lI + ∆lII = |
q l2 |
( |
1 |
− |
1 |
) = |
1 q l2 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
4 EA |
|
; |
|
EA |
|
4 |
8 |
8 |
EA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
δ4 =δ3 + ∆lIII |
= |
|
q l2 |
( |
1 |
− |
3 |
) |
= |
− |
1 q l2 |
; |
|
|
δ5 =δ |
4 + ∆lIY |
= |
q l |
2 |
|
1 |
|
+ |
1 |
) = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
EA |
8 |
8 |
4 |
|
EA |
|
|
|
EA |
(− |
4 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||

Этап 7. Построение эпюр N (z), σx (z), εx (z), δ(z)
РАЗНОВИДНОСТИ ЗАДАЧ
Наименование |
Расчетная схема |
Этапы основных особенностей решения |
Построение эпюр |
|
Этапы те же самые, но направления |
ВСФ в статически |
|
|
определимом прямом |
|
суммирования внешних сил и построения |
брусе при силовом |
|
|
|
|
|
нагружении перемен- |
|
эпюры перемещений меняются на |
ной распределенной |
|
|
нагрузкой при |
|
противоположное |
закреплении правого |
|
|
конца бруса |
|
|
